
- •А.М. ГОЛИКОВ
- •Учебное пособие:
- •Томск 2018
- •Учебное пособие
- •История развития криптографии
- •Основные характеристики открытого текста
- •Классификация шифров
- •Шифры перестановки
- •Шифр Хилла
- •Шифры сложной замены
- •Линейный конгруэнтный генератор
- •Регистр сдвига с линейной обратной связью
- •Блочные и поточные системы шифрования
- •Принципы построения блочных шифров
- •Основной шаг криптопреобразования.
- •Базовые циклы криптографических преобразований.
- •Основные режимы шифрования.
- •Простая замена
- •Гаммирование
- •Гаммирование с обратной связью
- •Выработка имитовставки к массиву данных.
- •Американский стандарт шифрования данных DES
- •Основные режимы шифрования
- •Блочный криптоалгоритм RIJNDAEL и стандарт AES
- •Математические предпосылки
- •Сложение
- •Описание криптоалгоритма
- •Раундовое преобразование
- •Атака “Квадрат”
- •Предпосылки
- •Базовая атака “Квадрат” на 4 раунда
- •Добавление пятого раунда в конец базовой атаки “Квадрат”
- •Добавление шестого раунда в начало базовой атаки “Квадрат”
- •Поточные системы шифрования
- •Поточные режимы блочных шифров
- •Строительные блоки поточных шифров
- •Регистры сдвига с обратной связью
- •Регистры сдвига с линейной обратной связью
- •Генераторы на основе LFSR
- •Регистры сдвига с нелинейной обратной связью
- •Регистры сдвига с обратной связью по переносу
- •Поточный шифр HC-128
- •Инициализация
- •Генерация ключевого потока
- •Поточный шифр Rabbit
- •Инициализация
- •Поточный шифр Salsa20
- •Хеш-функция Salsa20
- •Инициализация
- •Функция шифрования Salsa20
- •Поточный шифр SOSEMANUK
- •SERPENT и его производные
- •Инициализация
- •Генерация ключевого потока
- •Поточный шифр F-FCSR-H
- •Генерация ключевого потока
- •Инициализация
- •Поточный шифр Grain-128
- •Генерация ключевого потока
- •Инициализация
- •Поточный шифр MICKEY-128
- •Инициализация
- •Генерация ключевого потока
- •Поточный шифр Trivium
- •Инициализация
- •Генерация ключевого потока
- •Гаммирование
- •Гаммирование с обратной связью
- •Блочный шифр AES в поточном режиме
- •Функция зашифрования
- •Расширение ключа
- •Функция расшифрования
- •Режим обратной связи по шифртексту (CFB)
- •Режим обратной связи по выходу (OFB)
- •Режим счетчика (Counter mode)
- •Методы оценки качества алгоритмов поточного шифрования
- •1. Период
- •2. Криптоанализ шифров
- •3. Линейная сложность
- •4. Исчерпывающий поиск ключа
- •5. Time-memory-data trade-off атака
- •6. Корреляционная атака
- •Быстрая корреляционная атака
- •Алгебраическая атака
- •Атака различением
- •Статистический анализ гаммы шифров
- •Статистические свойства
- •Тестирование
- •Набор статистических тестов НИСТ
- •Частотный тест
- •Частотный тест внутри блока
- •Тест последовательностей
- •Тест наибольших последовательностей единиц в блоке
- •Тест рангов двоичных матриц
- •Спектральный тест
- •Тест сравнения непересекающихся шаблонов
- •Тест сравнения пересекающихся шаблонов
- •Тест сжатия алгоритмом Зива-Лемпела
- •Тест линейной сложности
- •Тест серий
- •Энтропийный тест
- •Тест совокупных сумм
- •Тест случайных отклонений
- •Вариант теста случайных отклонений
- •Анализ результатов тестирования
- •Исследование производительности шифров
- •Rabbit
- •Salsa20/12
- •Salsa20/12
- •Sosemanuk
- •Выводы
- •Цель работы Изучить криптографический стандарт шифрования ГОСТ 28147-89 и его особенности, познакомиться с различными режимами блочного шифрования.
- •Порядок выполнения работы
- •Контрольные вопросы
- •Интерфейс учебно-программного комплекса
- •Главное окно
- •Пункт меню “Файл”
- •Пункт меню “AES”
- •Режимы ECB, CBC, CFB, OFB
- •Режим ECB (Electronic Code Book – режим электронной кодовой книги)
- •Режим CBC (Ciphertext Block Chaining – режим сцепления блоков шифротекста)
- •Режим CFB (Ciphertext Feedback – обратная связь по шифротексту)
- •Режим OFB (Output Feedback – режим обратной связи по выходу)
- •Описание алгоритма
- •Безопасность
- •Программная реализация
- •Заключение
- •Общее описание лабораторной работы
- •Общий вид окна учебной программы
- •Требования к размещению файлов
- •Необходимые знания
- •Загрузка варианта
- •Выбор вероятных составляющих
- •Нахождение вероятной части ключа
- •Определение положения отводов
- •Поиск начального заполнения
- •Получение гаммы
- •Получение открытого текста
- •Отчет о проделанной работе
- •Сообщения выдаваемые в процессе работы
- •Сообщения об ошибках
- •Сообщения-вопросы
- •Критические ошибки
- •Пример
- •Асимметричные криптосистемы [8 -14]
- •Предпосылки появления асимметричных криптосистем
- •Обобщенная схема асимметричной крипосистемы
- •Алгебраическая обобщенная модель шифра
- •Односторонние функции
- •Факторизация
- •Дискретный логарифм
- •Криптосистема RSA
- •Основные определения и теоремы
- •Алгоpитм RSA
- •Процедуры шифрования и расшифрования в криптосистеме RSA
- •Криптосистема Эль-Гамаля
- •Комбинированный метод шифрования
- •Метод экспоненциального ключевого обмена Диффи-Хеллмана
- •Алгоритмы практической реализации криптосистем с открытым ключом
- •Возведение в степень по модулю m
- •Алгоритм Евклида вычисления НОД
- •Вычисление обратных величин в кольце целых чисел
- •Генерация простых чисел
- •Атаки на алгоритм RSA
- •Практическая часть
- •Лабораторная работа 1
- •Ход работы
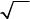
которых желательно иметь малое значение е и d. Например, при использовании системы RSA при защите электронных платежей с применением кредитных карточек естественным является требование использования небольших значений экспоненты d у владельца карточки и большого значения экспоненты e у центрального компьютера.
Однако выбор малых параметров е или d представляется небезопасным по ряду соображений. Если малым является секретный параметр d, то можно применить метод перебора малых значений до получения искомого числа d. А если малым является параметр е, то достаточно большое число открытых сообщений, удовлетворяющих неравенству
x |
e N , |
будут зашифровываться простым возведением в степень |
y x e ( m o d N ) |
и |
|
|
|
поэтому их можно найти путем извлечения корня степени е.
Другая аналогичная ситуация может сложиться, когда у нескольких абонентов используется одинаковая экспонента е. Тогда становится возможна атака на основе китайской теоремы об остатках (см. ниже).
Ход работы
1.Вычисляем n = [sqrt(N)] + 1. В поле A помещаем N, в поле B – 2; нажимаем кнопку «D
=A^(1/B)». В поле D заносится число 8112686, в первую строку таблицы – сообщение «[error]». Это свидетельствует, о том, что N не является квадратом целого числа.
2.t1 = n + 1. Возводим число t1 в квадрат: A: = 8112687, B: = 2, C: = 0 (возведение в квадрат будет производиться не по правилам модульной арифметики), нажимаем «D = A^B
mod |
C» |
=> |
D |
= |
t1^2 |
= |
65815690359969. |
Вычисляем |
|
w1 |
= |
t1^2 – N. Для |
этого A:= t1^2, B:= –N, |
затем нажимаем «D = |
A + B» => D = |
||||
= |
w1 |
= 18491912. |
Проверяем, |
является |
ли |
w1 квадратом целого |
числа: A:= w1, |
||
B:= 2, нажимаем «D = A^(1/B)» => в первой строке таблицы появляется сообщение «[error]», следовательно проделываем п. 2 заново с t2 = n + 2 и так далее, пока не найдем, что некое wi является квадратом целого числа.
3. При вычислении квадратного корня w5 первая строка таблицы остается пустой, а D =
sqrt(w5) |
= |
9132, |
что |
свидетельствует |
об |
успехе |
факторизации. |
t5 = 8112691. |
|
|
|
|
|
|
|
4. Вычисляем p = t5 + sqrt(w5); A:= t5, B:= sqrt(w5), нажимаем «D = A + B» => D = p = 8121823; q = t5 – sqrt(w5) = 8103559. Вычисляем
424
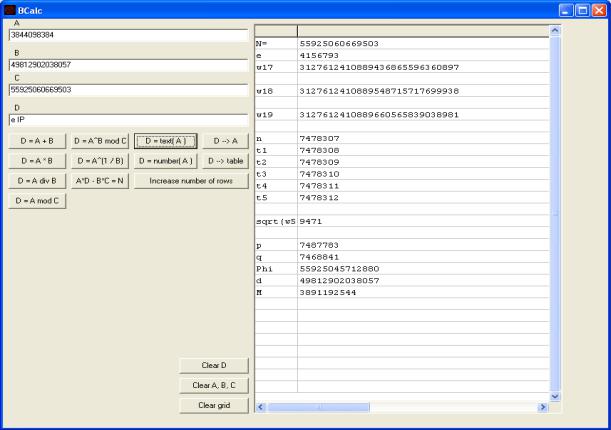
Phi(N) = |
(p – 1)(q – 1), A:= |
8121822, B:= |
8103558, нажимаем |
«D = A·B» => D = |
= Phi(N),ключи).В) |
= 65815655642676. |
Вычисляем |
d, как обратный к |
e: A:= e, B:= –1, |
C:= Phi(N), нажимаем «D = A^B mod C» => D = d = 12490789985101. |
|
|||
5. Производим дешифрацию шифрблока С: A:= C; B:= d; C:= N. Нажимаем «D = A^B mod C». В поле D находится исходное сообщение M = 3402418120. Переводим M в текстовый вид. Для этого A:= M, нажимаем «D = text(A)» => D = = «КМЗИ».
Вариант №20
Ответ: «зования протокола ТСР: фрагментация на уровне IP»
Вариант №23.
425
Ответ: «оптимальным МТU на уровне DLC маленький
Как видно из приведенных выше примеров (а также из примеров выполнения заданий лабораторных работ) выбор параметров криптосистемы является ответственной задачей. Параметры необходимо выбирать в строгом соответствии с требованиями. Существующими в настоящими время методами (и при использовании существующих в настоящее время вычислительных мощностей) атака на алгоритм и/или криптосистему возможна лишь при неудачном выборе параметров. В процессе выполнения заданий лабораторных работ вы убедитесь в обоснованности перечисленных требований к параметрам криптосистемы. В частности, необходимо обеспечить каждому пользователю уникальные значения p, q и уникальное значение e, удовлетворяющие требованиям, приведенным выше.
ЗАКЛЮЧЕНИЕ
426
В учебном пособии рассмотрены классические шифры, теория классических шифров, компьютерный практикум для классических шифров и задания на самостоятельную работу по классическим шифрам. Преставлены современные математические методы шифрования с секретным ключом, теория шифров с секретным ключом, компьютерный практикум для шифров с секретным ключом и задания на самостоятельную работу по шифрам с секретным ключо. Рассмотрены математические основы шифрования с открытым ключом, теория шифров с открытым ключом, компьютерный практикум для шифров с открытым ключом и задания на самостоятельную работу по шифрам с открытым ключом.
ЛИТЕРАТУРА
427

1.Алферов А.П., Зубов А.Ю., Кузьмин А.С., Черемушкин А.В. Основы криптографии
–М.: Гелиос АРВ, 2001. – 480 с.
2.Метлицкий Ю.В. Разработка программного комплекса для визуализации и анализа стандарта криптографической защиты AES, МИФИ 2003 г.
3.Зензин О.С., Иванов М.А. Стандарт криптографической защиты – AES. Конечные поля. – М: КУДИЦ-ОБРАЗ, 2002. -176 с.
4.Б. Шнайер «Прикладная криптография. 2-е издание. Протоколы, алгоритмы и исходные тексты на языке С». - М.: Изд-во "Триумф", 2002. - 816 с.
5.http://www.des-crypto.ru/cryptography/rc4/
6.Асосков А.В. и др. Поточные шифры. - М.: КУДИЦ-ОБРАЗ, 2003. - 336 с.
7.http://www.wisdom.weizmann.ac.il/~itsik/RC4/rc4.html
8.Романец Ю.В. Защита информации в компьютерных системах и сетях / Под ред. В.Ф. Шаньгина. - 2-е изд., перераб. и доп. - М.: Радио и связь, 2001. - 376 с.
9.RSA Laboratories // http://www.rsa.com/rsalabs/node.asp?id=2009
10.Алгоритм RSA : метод. указания к выполнению лабораторных работ для студентов спец. 090105 «Комплексное обеспечение информационной безопасности
автоматизированных систем» очной формы обучения / сост.: О. Н. Жданов, И. А. Лубкин ; Сиб. гос. аэрокосмич. ун-т. – Красноярск, 2007. – 38 с.
11.Diffie, D. N),ключи).Вew directions in Cryptography / D. Diffie, M.Hellman // IEEE Transactions on information theory. N),ключи).Вovember. 1976.
12.Rivest, R. A Method for obtaining digital signatures and public keyCryptosystems
/R. Rivest, A. Shamir, L. Adleman // Communications of the ACM. February. 1978.
13.Столингс, В. Криптография и защита сетей: принципы и практика
/В. Столингс ; пер. с англ. . – 2-е изд. – М. : Изд. дом «Вильямс», 2001. – 672 с.
14.Коблиц, Н. Курс теории чисел и криптографии / Н. Коблиц ; пер. с англ. М. А. Михайловой и В. Е. Тараканова ; под. ред. А. М. Зубкова. – М. : Науч. изд-во ТВП, 2001. – 254 с.
428
