
- •А.М. ГОЛИКОВ
- •Учебное пособие:
- •Томск 2018
- •Учебное пособие
- •История развития криптографии
- •Основные характеристики открытого текста
- •Классификация шифров
- •Шифры перестановки
- •Шифр Хилла
- •Шифры сложной замены
- •Линейный конгруэнтный генератор
- •Регистр сдвига с линейной обратной связью
- •Блочные и поточные системы шифрования
- •Принципы построения блочных шифров
- •Основной шаг криптопреобразования.
- •Базовые циклы криптографических преобразований.
- •Основные режимы шифрования.
- •Простая замена
- •Гаммирование
- •Гаммирование с обратной связью
- •Выработка имитовставки к массиву данных.
- •Американский стандарт шифрования данных DES
- •Основные режимы шифрования
- •Блочный криптоалгоритм RIJNDAEL и стандарт AES
- •Математические предпосылки
- •Сложение
- •Описание криптоалгоритма
- •Раундовое преобразование
- •Атака “Квадрат”
- •Предпосылки
- •Базовая атака “Квадрат” на 4 раунда
- •Добавление пятого раунда в конец базовой атаки “Квадрат”
- •Добавление шестого раунда в начало базовой атаки “Квадрат”
- •Поточные системы шифрования
- •Поточные режимы блочных шифров
- •Строительные блоки поточных шифров
- •Регистры сдвига с обратной связью
- •Регистры сдвига с линейной обратной связью
- •Генераторы на основе LFSR
- •Регистры сдвига с нелинейной обратной связью
- •Регистры сдвига с обратной связью по переносу
- •Поточный шифр HC-128
- •Инициализация
- •Генерация ключевого потока
- •Поточный шифр Rabbit
- •Инициализация
- •Поточный шифр Salsa20
- •Хеш-функция Salsa20
- •Инициализация
- •Функция шифрования Salsa20
- •Поточный шифр SOSEMANUK
- •SERPENT и его производные
- •Инициализация
- •Генерация ключевого потока
- •Поточный шифр F-FCSR-H
- •Генерация ключевого потока
- •Инициализация
- •Поточный шифр Grain-128
- •Генерация ключевого потока
- •Инициализация
- •Поточный шифр MICKEY-128
- •Инициализация
- •Генерация ключевого потока
- •Поточный шифр Trivium
- •Инициализация
- •Генерация ключевого потока
- •Гаммирование
- •Гаммирование с обратной связью
- •Блочный шифр AES в поточном режиме
- •Функция зашифрования
- •Расширение ключа
- •Функция расшифрования
- •Режим обратной связи по шифртексту (CFB)
- •Режим обратной связи по выходу (OFB)
- •Режим счетчика (Counter mode)
- •Методы оценки качества алгоритмов поточного шифрования
- •1. Период
- •2. Криптоанализ шифров
- •3. Линейная сложность
- •4. Исчерпывающий поиск ключа
- •5. Time-memory-data trade-off атака
- •6. Корреляционная атака
- •Быстрая корреляционная атака
- •Алгебраическая атака
- •Атака различением
- •Статистический анализ гаммы шифров
- •Статистические свойства
- •Тестирование
- •Набор статистических тестов НИСТ
- •Частотный тест
- •Частотный тест внутри блока
- •Тест последовательностей
- •Тест наибольших последовательностей единиц в блоке
- •Тест рангов двоичных матриц
- •Спектральный тест
- •Тест сравнения непересекающихся шаблонов
- •Тест сравнения пересекающихся шаблонов
- •Тест сжатия алгоритмом Зива-Лемпела
- •Тест линейной сложности
- •Тест серий
- •Энтропийный тест
- •Тест совокупных сумм
- •Тест случайных отклонений
- •Вариант теста случайных отклонений
- •Анализ результатов тестирования
- •Исследование производительности шифров
- •Rabbit
- •Salsa20/12
- •Salsa20/12
- •Sosemanuk
- •Выводы
- •Цель работы Изучить криптографический стандарт шифрования ГОСТ 28147-89 и его особенности, познакомиться с различными режимами блочного шифрования.
- •Порядок выполнения работы
- •Контрольные вопросы
- •Интерфейс учебно-программного комплекса
- •Главное окно
- •Пункт меню “Файл”
- •Пункт меню “AES”
- •Режимы ECB, CBC, CFB, OFB
- •Режим ECB (Electronic Code Book – режим электронной кодовой книги)
- •Режим CBC (Ciphertext Block Chaining – режим сцепления блоков шифротекста)
- •Режим CFB (Ciphertext Feedback – обратная связь по шифротексту)
- •Режим OFB (Output Feedback – режим обратной связи по выходу)
- •Описание алгоритма
- •Безопасность
- •Программная реализация
- •Заключение
- •Общее описание лабораторной работы
- •Общий вид окна учебной программы
- •Требования к размещению файлов
- •Необходимые знания
- •Загрузка варианта
- •Выбор вероятных составляющих
- •Нахождение вероятной части ключа
- •Определение положения отводов
- •Поиск начального заполнения
- •Получение гаммы
- •Получение открытого текста
- •Отчет о проделанной работе
- •Сообщения выдаваемые в процессе работы
- •Сообщения об ошибках
- •Сообщения-вопросы
- •Критические ошибки
- •Пример
- •Асимметричные криптосистемы [8 -14]
- •Предпосылки появления асимметричных криптосистем
- •Обобщенная схема асимметричной крипосистемы
- •Алгебраическая обобщенная модель шифра
- •Односторонние функции
- •Факторизация
- •Дискретный логарифм
- •Криптосистема RSA
- •Основные определения и теоремы
- •Алгоpитм RSA
- •Процедуры шифрования и расшифрования в криптосистеме RSA
- •Криптосистема Эль-Гамаля
- •Комбинированный метод шифрования
- •Метод экспоненциального ключевого обмена Диффи-Хеллмана
- •Алгоритмы практической реализации криптосистем с открытым ключом
- •Возведение в степень по модулю m
- •Алгоритм Евклида вычисления НОД
- •Вычисление обратных величин в кольце целых чисел
- •Генерация простых чисел
- •Атаки на алгоритм RSA
- •Практическая часть
- •Лабораторная работа 1
- •Ход работы
3.ШИФРОВАНИЕ С ОТКРЫТЫМ КЛЮЧОМ
3.1.Теория шифров с открытым ключом
Асимметричные криптосистемы [8 -14]
Предпосылки появления асимметричных криптосистем
Появлению нового направления в криптологии - асимметричной криптографии с открытым ключом - способствовали две проблемы, которые не удавалось решить в рамках классической симметричной одноключевой криптографии.
333
Первая из этих проблем связана с распространением секретных ключей. Как передать участникам обмена информацией сменяемые секретные ключи, которые требуются им для осуществления этого обмена? В общем случае для передачи ключа опять же требуется использование какой-то криптосистемы, то есть задача в рамках симметричной криптографии неразрешима.
Вторая из этих проблем связана с распространением электронного документооборота. Возникла проблема обеспечения подлинности и авторства электронных документов. В обычном, бумажном документообороте эта прооблема решается с помощью подписи на бумаге. Подделать подпись человека на бумаге совсем не просто, а скопировать цепочку цифр на ЭВМ - несложная операция. Возникла проблема цифровой подписи, которая бы выполняла все те задачи, которые выполняет подпись, поставленная на документе рукой. Обе эти проблемы были успешно решены с помощью криптографии с открытыми ключами. В опубликованной в 1976 г. статье "Новые направления в криптографии" У.Диффи и М.Хеллман впервые показали, что секретная связь возможна без передачи секретного ключа между отправителем и получателем.
На основе результатов, полученных классической и современной алгеброй, были предложены системы с открытым ключом, называемые также асимметричными криптосистемами.
Суть их состоит в том, что каждым адресатом ИС генерируются два ключа, связанные между собой по определенному правилу. Один ключ объявляется открытым, а другой закрытым. Открытый ключ публикуется и доступен любому, кто желает послать сообщение
334
|
|
криптоаналитик |
|
|
Отправитель |
|
Открытый |
|
Получатель |
сообщений |
шифратор |
канал |
дешифратор |
сообщений |
|
|
|
Секретный |
|
|
|
|
ключ |
|
|
|
Аутентичный |
Генератор |
|
|
|
канал |
ключей |
|
|
|
|
Открытый |
|
|
|
|
ключ |
|
|
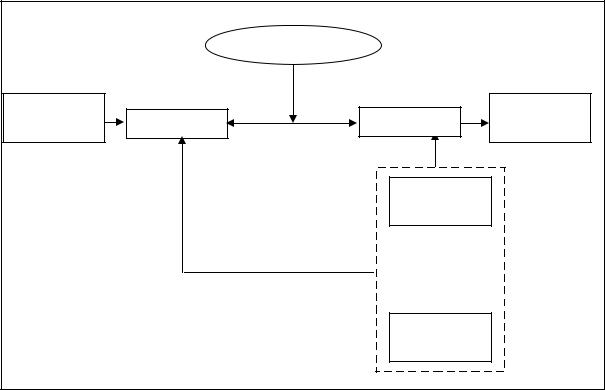
Рис. 3.1. Обобщенная схема асимметричной крипосистемы |
|||
адресату. Секретный ключ сохраняется в тайне. Если генератор ключей расположить на стороне получателя, то отпадает необходимость пересылки секретного ключа по каналу связи.
Исходный текст шифруется открытым ключом адресата и передается ему. Зашифрованный текст в принципе не может быть расшифрован тем же открытым ключом. Дешифрование сообщения возможно только с использованием закрытого ключа, который известен только самому адресату. Таким образом, не требуется секретный канал связи для передачи ключа, но необходимо обеспечить подлинность открытого ключа, так как его искажение или подмена не позволит расшифровать информацию на парном с ним закрытом ключе. Кроме того, замена злоумышленником законного открытого ключа на свой открытый ключ предоставляет ему полный доступ к шифруемой информации.
Обобщенная схема асимметричной крипосистемы
Ниже (рис.3.1) приведена обобщенная схема асимметричной крипосистемы.
Здесь для передачи ключа используется открытый канал связи, обеспечивающий аутентичность передаваемой информации.
Чтобы гарантировать надежную защиту информации, к системам с открытым ключом (СОК) предъявляются два важных и очевидных требования:
335
1.Преобразование исходного текста должно быть необратимым и исключать его восстановление на основе открытого ключа.
2.Определение закрытого ключа на основе открытого также должно быть невозможным на современном технологическом уровне. При этом желательна точная нижняя оценка сложности раскрытия шифра.
Алгоритмы шифрования с открытым ключом получили широкое распространение в современных информационных системах. Их используют в следующих основных напрвлениях:
1.Как самостоятельные средства защиты передаваемых и хранимых данных.
2.Как средства для распределения криптографических ключей. Алгоритмы асимметричных крипосистем более трудоемки, чем традиционные криптосистемы. Поэтому часто на практике имеет смысл с помощью асимметричных крипосистем распределять ключи, объем которых незначителен. А потом с помощью менее трудоемких симметричных алгоритмов осуществлять обмен большими информационными потоками.
3.Как средства аутентификации пользователей информационных систем, в том числе для решения проблемы электронной подписи.
4.Как средства для построения сложных криптографических протоколов для решения различных задач защиты инфомации в современных информационных системах.
Алгебраическая обобщенная модель шифра
Ранее мы рассматривали алгебраическую модель шифра К.Шеннона как трехосновную универсальную алгебру А=(М,К,С,Е), где
M - множество открытых текстов, К - множество ключей,
C - множество криптограмм и
Е – инъективная (взаимно однозначная) функция шифрования: Еk: МхК С Ek(m)=c, где m M, k K, c C.
Для того, чтобы эта модель могла быть применима к асимметричным криптографическим системам, необходимо ее расширение. Основная концептуальная идея построения такой модели, естественна и очевидна. Она состоит в отдельном описании моделей двух шифров: шифра шифрования и шифра расшифрования, совокупность которых и составляет обобщенную алгебраическую модель шифра.
336
Шифром зашифрования (алгеброй зашифрования) назовем алгебру
Аш=(М, Мс, Кш С, Сс, Е), |
где |
множество Мс М трактуется как подмножество всех содержательных текстов из множества «открытых текстов» M.
функция шифрования Е осуществляет отображение МхКш на С:
Е: МхКш С, Ек(m)=c,
то есть является сюрьективной, причем k Кш отображение Еk(m) инъективно (образы двух различных элементов различны), а множество Сс состоит из шифрограмм, которые могут быть получены в результате шифрования содержательных текстов: Сс =Е(McхKш), то есть результатов шифрования тех открытых текстов m, для которых определено значение Еk(m) для всех ключей шифра k Кш.
Введение подмножества Мс М как множества содержательных текстов позволяет корректно вводить критерии на содержательные тексты.
Таким образом, шифр зашифрования есть некоторое уточнение модели шифра Шеннона А=(М,Кш,С,Е).
Шифром расшифрования (алгеброй расшифрования) для Аш назовем алгебру Ар=(Мр, Кр, Ср, D), где
C Ср и введение множества Cp — шифртекстов «правильных» сообщений (а точнее, Cp\C — множества искаженных шифртекстов) обеспечивает возможность описания реакции приемной стороны на поступление искаженного шифрованного сообщения cp C;
М Мр, и введение множества Мp\М обеспечивает возможность описания результата расшифрования приемной стороной искаженного шифрованного сообщения cp C;
функция дешифрования D- сюрьективное отображение
D:Cpx Кр Мр, Dk(с)= m,
для которого выполняются следующие условия:
1)существует биекция f: Кш Кр;
2)для любых m M, k Кш из условия Еk(m)=c вытекает D(c,f (k))=m.
При отсутствии искажений в канале связи функция расшифрования D полностью
определена на всем множестве CхКр.
337
