
- •А.М. ГОЛИКОВ
- •Учебное пособие:
- •Томск 2018
- •Учебное пособие
- •История развития криптографии
- •Основные характеристики открытого текста
- •Классификация шифров
- •Шифры перестановки
- •Шифр Хилла
- •Шифры сложной замены
- •Линейный конгруэнтный генератор
- •Регистр сдвига с линейной обратной связью
- •Блочные и поточные системы шифрования
- •Принципы построения блочных шифров
- •Основной шаг криптопреобразования.
- •Базовые циклы криптографических преобразований.
- •Основные режимы шифрования.
- •Простая замена
- •Гаммирование
- •Гаммирование с обратной связью
- •Выработка имитовставки к массиву данных.
- •Американский стандарт шифрования данных DES
- •Основные режимы шифрования
- •Блочный криптоалгоритм RIJNDAEL и стандарт AES
- •Математические предпосылки
- •Сложение
- •Описание криптоалгоритма
- •Раундовое преобразование
- •Атака “Квадрат”
- •Предпосылки
- •Базовая атака “Квадрат” на 4 раунда
- •Добавление пятого раунда в конец базовой атаки “Квадрат”
- •Добавление шестого раунда в начало базовой атаки “Квадрат”
- •Поточные системы шифрования
- •Поточные режимы блочных шифров
- •Строительные блоки поточных шифров
- •Регистры сдвига с обратной связью
- •Регистры сдвига с линейной обратной связью
- •Генераторы на основе LFSR
- •Регистры сдвига с нелинейной обратной связью
- •Регистры сдвига с обратной связью по переносу
- •Поточный шифр HC-128
- •Инициализация
- •Генерация ключевого потока
- •Поточный шифр Rabbit
- •Инициализация
- •Поточный шифр Salsa20
- •Хеш-функция Salsa20
- •Инициализация
- •Функция шифрования Salsa20
- •Поточный шифр SOSEMANUK
- •SERPENT и его производные
- •Инициализация
- •Генерация ключевого потока
- •Поточный шифр F-FCSR-H
- •Генерация ключевого потока
- •Инициализация
- •Поточный шифр Grain-128
- •Генерация ключевого потока
- •Инициализация
- •Поточный шифр MICKEY-128
- •Инициализация
- •Генерация ключевого потока
- •Поточный шифр Trivium
- •Инициализация
- •Генерация ключевого потока
- •Гаммирование
- •Гаммирование с обратной связью
- •Блочный шифр AES в поточном режиме
- •Функция зашифрования
- •Расширение ключа
- •Функция расшифрования
- •Режим обратной связи по шифртексту (CFB)
- •Режим обратной связи по выходу (OFB)
- •Режим счетчика (Counter mode)
- •Методы оценки качества алгоритмов поточного шифрования
- •1. Период
- •2. Криптоанализ шифров
- •3. Линейная сложность
- •4. Исчерпывающий поиск ключа
- •5. Time-memory-data trade-off атака
- •6. Корреляционная атака
- •Быстрая корреляционная атака
- •Алгебраическая атака
- •Атака различением
- •Статистический анализ гаммы шифров
- •Статистические свойства
- •Тестирование
- •Набор статистических тестов НИСТ
- •Частотный тест
- •Частотный тест внутри блока
- •Тест последовательностей
- •Тест наибольших последовательностей единиц в блоке
- •Тест рангов двоичных матриц
- •Спектральный тест
- •Тест сравнения непересекающихся шаблонов
- •Тест сравнения пересекающихся шаблонов
- •Тест сжатия алгоритмом Зива-Лемпела
- •Тест линейной сложности
- •Тест серий
- •Энтропийный тест
- •Тест совокупных сумм
- •Тест случайных отклонений
- •Вариант теста случайных отклонений
- •Анализ результатов тестирования
- •Исследование производительности шифров
- •Rabbit
- •Salsa20/12
- •Salsa20/12
- •Sosemanuk
- •Выводы
- •Цель работы Изучить криптографический стандарт шифрования ГОСТ 28147-89 и его особенности, познакомиться с различными режимами блочного шифрования.
- •Порядок выполнения работы
- •Контрольные вопросы
- •Интерфейс учебно-программного комплекса
- •Главное окно
- •Пункт меню “Файл”
- •Пункт меню “AES”
- •Режимы ECB, CBC, CFB, OFB
- •Режим ECB (Electronic Code Book – режим электронной кодовой книги)
- •Режим CBC (Ciphertext Block Chaining – режим сцепления блоков шифротекста)
- •Режим CFB (Ciphertext Feedback – обратная связь по шифротексту)
- •Режим OFB (Output Feedback – режим обратной связи по выходу)
- •Описание алгоритма
- •Безопасность
- •Программная реализация
- •Заключение
- •Общее описание лабораторной работы
- •Общий вид окна учебной программы
- •Требования к размещению файлов
- •Необходимые знания
- •Загрузка варианта
- •Выбор вероятных составляющих
- •Нахождение вероятной части ключа
- •Определение положения отводов
- •Поиск начального заполнения
- •Получение гаммы
- •Получение открытого текста
- •Отчет о проделанной работе
- •Сообщения выдаваемые в процессе работы
- •Сообщения об ошибках
- •Сообщения-вопросы
- •Критические ошибки
- •Пример
- •Асимметричные криптосистемы [8 -14]
- •Предпосылки появления асимметричных криптосистем
- •Обобщенная схема асимметричной крипосистемы
- •Алгебраическая обобщенная модель шифра
- •Односторонние функции
- •Факторизация
- •Дискретный логарифм
- •Криптосистема RSA
- •Основные определения и теоремы
- •Алгоpитм RSA
- •Процедуры шифрования и расшифрования в криптосистеме RSA
- •Криптосистема Эль-Гамаля
- •Комбинированный метод шифрования
- •Метод экспоненциального ключевого обмена Диффи-Хеллмана
- •Алгоритмы практической реализации криптосистем с открытым ключом
- •Возведение в степень по модулю m
- •Алгоритм Евклида вычисления НОД
- •Вычисление обратных величин в кольце целых чисел
- •Генерация простых чисел
- •Атаки на алгоритм RSA
- •Практическая часть
- •Лабораторная работа 1
- •Ход работы
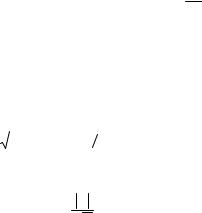
Спектральный тест
Цель спектрального теста или теста дискретного преобразования Фурье (the discrete Fourier transform (DFT) (spectral) test) – определить в тестируемой последовательности периодические элементы (т.е. повторяющиеся образцы, идущие друг за другом), которые указывали бы на отклонение от случайности.
Из тестируемой двоичной последовательности длиной n бит формируется последовательность X = x1, x2, …, xn, где xi = +1, если i-й элемент исходной последовательности равен 1 и xi = –1, если i-й элемент равен 0.
К полученной последовательности X применяется дискретное преобразование Фурье S = DFT(X). В результате будет получена последовательность комплексных переменных – гармоники. Затем вычисляется значение M = modulus (S’) S’, где S’ – подпоследовательность, состоящая из первых n/2 элементов в S, а функция modulus производит последовательность высот выбросов преобразования Фурье.
Вычисляются значения T 
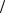 3n , соответствующее 95% пороговому уровню высот выбросов, и N0 = 0,95n/2 – ожидаемое количество высот выбросов меньших, чем T.
3n , соответствующее 95% пороговому уровню высот выбросов, и N0 = 0,95n/2 – ожидаемое количество высот выбросов меньших, чем T.
Вычисляется N1 – фактически наблюдаемое число высот выбросов в M меньших, чем T. Вычисляется тестовая статистика
d |
|
N1 N0 |
||
|
|
|
. |
|
|
|
|
||
n 0,95 0,05 2 |
||||
Затем вычисляется значение P-тест,value
d
P-тест,value = erfc .

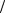 2
2
Слишком маленькое значение d будет указывать на то, что слишком мало высот (< 95%) меньше, чем T, и слишком много высот (> 5%) больше, чем T.
Тест сравнения непересекающихся шаблонов
Цель теста сравнения непересекающихся шаблонов (the non-overlapping template matching test) – выявить последовательности, в которых слишком часто встречается заданный непериодический образец (шаблон).
|
|
n |
|
Тестируемая двоичная последовательность длиной n бит разбивается на |
N |
|
|
|
|||
|
|
M |
|
непересекающихся блоков длиной M бит каждый.
Поиск шаблонов производится следующим образом: каждый M-битовый блок просматривается при помощи m-битового окна. Биты в этом окне сравниваются с шаблоном. Если совпадения нет, то окно сдвигается на 1 бит дальше по последовательности, а если
232
совпадение есть, то окно сдвигается на m бит. Затем поиск возобновляется. Число появлений шаблона в j-м блоке, j = 1, …, N, подсчитывается и записывается в Wj.
При предположении о случайности вычисляются теоретические значения
|
M m 1 |
|
|
|
|
2 |
|
|
|
|
|
1 |
|
2m 1 |
|
|||||
|
|
|
|
и |
|
|
|
M |
|
|
|
|
. |
|||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
2m |
|
|
|
|
|
|
|
|
|
|
|
|
|
2m |
|
2m |
|
||
Вычисляется тестовая статистика |
|
|||||||||||||||||||
2 obs Wj |
|
2 |
|
2 |
|
. |
|
|
|
|
|
|
||||||||
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Затем вычисляется значение P-тест,value |
|
|||||||||||||||||||
|
|
igamc N |
, |
2 |
obs |
|
|
|
||||||||||||
P-тест,value = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
||
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
В данном тесте вычисляется множество значений P-тест,value, т.к. для каждого из шаблонов вычисляется одно значений P-тест,value. Для m = 10 может быть вычислено до 284 значений P-тест, value.
Малое значение P-тест,value (< 0,01) означает, что возможные шаблонны встречаются в последовательности неравномерно.
Тест сравнения пересекающихся шаблонов
Цель теста сравнения пересекающихся шаблонов (the overlapping template matching test) – выявить последовательности, в которых слишком часто встречается заданный непериодический образец.
|
|
n |
|
Тестируемая двоичная последовательность длиной n бит разбивается на |
N |
|
|
|
|||
|
|
M |
|
непересекающихся блоков длиной M бит каждый. |
|
|
|
Вданном тесте, как и в предыдущем, при поиске шаблонов каждый M-битовый блок просматривается при помощи m-битового окна. Биты в этом окне сравниваются с шаблоном. Если совпадения нет, то окно сдвигается на 1 бит дальше по последовательности. Отличие от предыдущего теста заключается в том, что если совпадение есть, то окно сдвигается не на m бит, а только на 1 бит. Затем поиск возобновляется.
Впроцессе просмотра m-битовых окон для каждого M-битового блока производится изменение счетчиков vi, i = 1, …, 5, следующим образом: v0 увеличивается, если шаблон в M- битовом блоке не встречается, v1 увеличивается, если шаблон в M-битовом блоке встречается один раз, v2 увеличивается, если шаблон в M-битовом блоке встречается два раза и т.д.
Вычисляются значения и , которые используются для вычисления теоретических вероятностей i
233
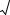
M m 1 |
и |
. |
2m |
|
2 |
Вычисляется тестовая статистика
5 |
vi N i |
2 |
|
2 obs |
|
. |
|
N i |
|
||
i 0 |
|
|
Затем вычисляется значение P-тест,value
|
igamc N |
, |
2 |
obs |
|||
P-тест,value = |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
2 |
|
|
|
2 |
|||
|
|
|
|
|
|
||
Универсальный статистический тест Маурера
Цель универсального статистического теста Маурера (Maurer’s “universal statistical” test)
– определить может ли последовательность быть значительно сжата без потери информации Тестируемая двоичная последовательность длиной n бит разбивается на две части:
первая часть (инициализирующая) состоит из Q L-битовых непересекающихся блоков, а
|
|
n |
|
|
вторая часть (тестовая) состоит из K L-битовых непересекающихся блоков, |
K |
|
|
Q . |
|
||||
|
|
L |
|
|
Биты, остающиеся в конце последовательности и не формирующие полный L-битовый блок, отбрасываются.
Инициализирующая часть используется для формирования таблицы, где каждому возможному L-битовому значению соответствует отдельный столбец. В первой строке таблицы отмечается номер i (i = 1, …, Q) последнего блока, в котором появилось соответствующее L-битовое значение. То есть Tj = i – содержимое j-ой ячейки таблицы, где j
– десятичное представление i-го L-битового блока.
Затем исследуется каждый блок тестовой части. Определяется количество блоков между текущим блоком и последним его появлением, т.е. (i – Tj), и производится обновление таблицы: Tj = i.
Вычисляется тестовая статистика
|
1 |
Q K |
|
|
|
|
|
|
|
|
|
fn |
log2 i Tj . |
|
|
|
|
||||||
|
|
|
|
|
|||||||
|
K i Q 1 |
|
|
|
|
|
|
|
|
||
Затем вычисляется значение P-тест,value |
|
|
|
|
|||||||
|
|
|
|
fn exðectedValue L |
|
|
|
|
|||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
P-тест,value |
= erfc |
|
|
2 |
|
|
|
, |
|||
|
|
|
|
|
|
|
|
|
|||
где expectedValue(L) и – значения, взятые из таблиц предвычисленных значений.
234
Тест сжатия алгоритмом Зива-Лемпела
Цель теста сжатия алгоритмом Зива-Лемпела (the Lempel-Ziv compression test) – определить как сильно тестируемая последовательность может быть сжата.
Из тестируемой двоичной последовательности длиной n бит, выбираются последовательные непересекающихся слова, формирующие словарь. Подсчитывается Wobs – число слов в словаре.
Затем вычисляется значение P-тест,value
1 |
|
W |
obs |
|
||
P-тест,value = 2 |
erfc |
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
. |
|||
Значения для и можно найти в [47_N),ключи).ВIST_STS].
Тест линейной сложности
Цель теста линейной сложности (the linear complexity test) – определить достаточно ли сложна последовательность, чтобы считаться случайной.
|
|
n |
|
Тестируемая двоичная последовательность длиной n бит разбивается на |
N |
|
|
|
|||
|
|
M |
|
непересекающихся блоков длиной M бит каждый. |
|
|
|
С помощью алгоритма Берлекампа-Месси определяется линейная сложность Li каждого из N блоков, i = 1, …, N. Li – это длина самого короткого LFSR, который способен сгенерировать последовательность бит i-го блока.
При предположении о случайности вычисляется теоретическое значение
|
M |
|
9 1 M 1 |
|
M |
|
2 |
|
|
|
|
3 |
9 . |
||||
2 |
36 |
2M |
|
|
||||
|
|
|
|
|
||||
Для каждого блока вычисляется значение Ti Ti = (–1)M (Li – ) + 2/9.
Используя вычисленные значения Ti, определяются значения v0, …, v6 следующим
образом |
|
|
|
|
|
|
|
|
|
Если |
Ti – 2,5, |
то |
v0 увеличивается на 1 |
||||||
|
|
– 2,5 |
< Ti – 1,5, |
|
v1 увеличивается на 1 |
||||
|
|
– 1,5 |
< Ti – 0,5, |
|
v2 увеличивается на 1 |
||||
|
|
– 0,5 |
< Ti 0,5, |
|
v3 |
увеличивается на 1 |
|||
|
|
0,5 |
< Ti 1,5, |
|
v4 |
увеличивается на 1 |
|||
|
|
1,5 |
< Ti 2,5, |
|
v5 |
увеличивается на 1 |
|||
|
|
2,5 |
< Ti, |
|
v6 |
увеличивается на 1 |
|||
Вычисляется тестовая статистика |
|
|
|
||||||
K |
vi |
N i |
2 |
|
|
|
|
|
|
2 obs |
|
. |
|
|
|
|
|
||
N i |
|
|
|
|
|
|
|||
i 0 |
|
|
|
|
|
|
|
||
235
