1. КЛАССИЧЕСКИЕ ШИФРЫ 1.1.Теория классических шифров
Основные характеристики открытого текста
Криптография занимается защитой сообщений, содержащихся на некотором материальном носителе. При этом сами сообщения представляют собой последовательности знаков (или слова) некоторого алфавита. Различают естественные алфавиты, например русский или английский, и специальные алфавиты (цифровые, буквенно-цифровые), например двоичный алфавит, состоящий из символов 0 и 1. В свою очередь, естественные алфавиты также могут отличаться друг от друга даже для данного языка.
Алфавиты открытых сообщений Наиболее привычны буквенные алфавиты, например русский, английский и т. д.
Приведем сведения об алфавитах некоторых естественных европейских языков. Полный русский алфавит состоит из 33 букв:
А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ъ Ы Ь Э Ю Я Вместе с тем используются и сокращенные русские алфавиты, содержащие 32, 31 или 30
букв. Можно отождествить буквы Е и Ё, И и Й, Ь и Ъ. часто бывает удобно включить в алфавит знак пробела между словами, в качестве которого можно взять, например, символ “–”.
Английский алфавит состоит из 26 букв:
А В C D E F G H I J K L M N),ключи).В O P Q R S T U V W X Y Z
Иногда используется сокращенный 25-буквенный алфавит, в котором отождествлены буквы I и J.
Любопытно отметить, что полинезийский язык Самоа имеет алфавит, содержащий всего 16 букв, из которых около 60% – гласных. В арабском языке и иврите согласные вообще не используются. Они опускаются в письменном тексте и восстанавливаются читателем по смыслу.
В вычислительной технике распространены 128-битовые и 256-битовые алфавиты, использующие представление знаков алфавита в виде 7- или 8-значных двоичных комбинаций.
Наиболее известен код ASCII (American Standart Code for Information Interchange) – американский стандартный код информационного обмена.
Буквенный алфавит, в котором буквы расположены в их естественном порядке, обычно называют нормальным алфавитом. В противном случае говорят о смешанных алфавитах. В
свою очередь, смешанные алфавиты делят на систематически перемешанные алфавиты и
45
случайные алфавиты. К первым относят алфавиты, полученные из нормального на основе некоторого правила, ко вторым – алфавиты, буквы которых следуют друг за другом в хаотическом (или случайном) порядке.
Смешанные алфавиты обычно используются в качестве нижней строки подстановки, представляющей собой ключ шифра простой замены. Для запоминания ключа (это надежнее, чем хранение ключа на некотором носителе) применяется несложная процедура перемешивания алфавита, например, основанная на ключевом слове.
Частотные характеристики текстовых сообщений Криптоанализ любого шифра невозможен без учета особенностей текстов сообщений,
подлежащих шифрованию. Глубинные закономерности текстовых сообщений исследуются в теории информации. Наиболее важной для криптографии характеристикой текстов является избыточность текста, введенная К. Шенноном. Именно избыточность открытого текста, проникающая в шифртекст, является основной слабостью шифра.
Более простыми характеристиками текстов, используемыми в криптоанализе, являются такие характеристики, как повторяемость букв, пар букв (6играмм) и вообще m-тест,ок (m-тест, грамм), сочетаемость букв друг с другом, чередование гласных и согласных и некоторые другие. Такие характеристики изучаются на основе эмпирических наблюдений текстов достаточно большой длины.
Для установления статистических закономерностей проводилась большая серия экспериментов по оценке вероятностей появления в открытом тексте фиксированных m- грамм (для небольших значений m).
Суть экспериментов состоит в подсчете чисел вхождений каждой из nm возможных m- грамм в достаточно длинных открытых текстах Т = t1 t2 … tl, составленных из букв алфавита {a1, a2, …, an}. При этом просматриваются подряд идущие m-граммы текста:
t1 t2 … tm, t2 t3 … tm+1, … tl–m+1 tl–m+2 … tl.
Если (аi1 аi2 … аim) – число появлений m-граммы аi1 аi2 … аim в тексте T, а L – общее число подсчитанных m-грамм, то опыт показывает, что при достаточно больших L частоты
ai1ai 2 ...aim
L
(2)
для данной m-граммы мало отличаются друг от друга. В силу этого относительную частоту (1.1) считают приближением вероятности P (аi1 аi2 … аim) появления данной m- граммы в случайно выбранном месте текста (такой подход принят при статистическом определении вероятности). Например, при m = 1 хорошее приближение вероятностей
появления букв достигается на текстах длины в несколько тысяч букв. 46
Некоторая разница значений частот в приводимых в различных источниках таблицах объясняется тем обстоятельством, что частоты существенно зависят не только от длины текста, но и от его характера. Так, в технических текстах редкая буква Ф может стать довольно частой в связи с частым использованием таких слов, как функция, дифференциал,
диффузия, коэффициент и т. п.
Еще большие отклонения от нормы в частоте употребления отдельных букв наблюдаются в некоторых художественных произведениях, особенно в стихах. Поэтому для надежного определения средней частоты буквы желательно иметь набор различных текстов, заимствованных из различных источников. Вместе с тем, как правило, подобные отклонения незначительны, и в первом приближении ими можно пренебречь.
В связи с этим подобные таблицы, используемые в криптографии, должны составляться с учетом характера переписки.
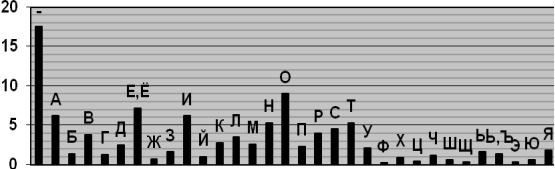
Для русского языка частоты (в порядке убывания) знаков алфавита, в котором отождествлены Е с Ё, Ь с Ъ, а также имеется знак пробела (–) между словами.
Рис. 1.4. Диаграмма частот букв русского языка Имеется мнемоническое правило запоминания десяти наиболее частых букв русского
алфавита. Эти буквы. СОС1ЗВляюг нелепое слово СЕНОВАЛИТР. Можно также предложить аналогичный способ запоминания частых букв английского языка, например, с помощью слова TETRIS-HON),ключи).ВDA.
Устойчивыми являются также частотные характеристики биграмм, триграмм и четырехграмм осмысленных текстов.
Хорошие таблицы k-гpaмм легко получить, используя тексты электронных версий многих книг, содержащихся на СD-дисках.
Для получения более точных сведений об открытых текстах можно строить и анализировать таблицы k-гpaмм при k > 2, однако для учебных целей вполне достаточно ограничиться биграммами. Неравновероятность k-грамм (и даже слов) тесно связана с характерной особенностью открытого текста – наличием в нем большого числа повторений отдельных фрагментов текста: корней, окончаний, суффиксов, слов и фраз. Так, для русского
47
языка такими привычными фрагментами являются наиболее частые биграммы и триграммы: СТ, НО, ЕН, ТО, НА, ОВ, НИ, РА, ВО, КО, СТО, ЕНО, НОВ, ТОВ, ОВО, ОВА Полезной является информация о сочетаемости букв, то есть о предпочтительных связях
букв друг с другом, которую легко извлечь из таблиц частот биграмм.
Имеется в виду таблица, в которой слева и справа от каждой буквы расположены наиболее предпочтительные “соседи” (в порядке убывания частоты соответствующих биграмм). В таких таблицах о6ычно указывается также доля гласных и согласных букв (в процентах), предшествующих (или следующих за) данной букве.
При анализе сочетаемости букв друг с другом следует иметь в виду зависимость появления букв в открытом тексте от значительного числа предшествующих букв. Для анализа этих закономерностей используют понятие условной вероятности.
Наблюдения над открытыми текстами показывают, что для условных вероятностей выполняются неравенства
p (ai1) p (ai1 / ai2), p (ai1 / ai2) p (ai1 / ai2 ai3),… .
Систематически вопрос о зависимости букв алфавита в открытом тексте от предыдущих букв исследовался известным русским математиком А. А. Марковым (1856 – 1922). Он доказал, что появления букв в открытом тексте нельзя считать независимыми друг от друга. В связи с этим А. А. Марковым отмечена еще одна устойчивая закономерность открытых текстов, связанная с чередованием гласных и согласных букв. Им были подсчитаны частоты встречаемости биграмм вида гласная-гласная (г, г), гласная-согласная (г, с), согласнаягласная (с, г), согласная-согласная (с, с) в русском тексте длиной в 105 знаков.
Из этой таблицы видно, что для русского языка характерно чередование гласных и согласных, причем относительные частоты могут служить приближениями соответствующих условных и безусловных вероятностей:
p (г/с) 0,663, |
p (с/г) 0,872 |
p (г) 0,432, |
p (с) 0,568. |
После А. А. Маркова зависимость появления букв текста вслед за несколькими предыдущими исследовал методами теории информации К. Шеннон. Фактически им было показано, в частности, что такая зависимость ощутима на глубину приблизительно в 30 знаков, после чего она практически отсутствует.
Приведенные выше закономерности имеют место для обычных “читаемых” открытых текстов, используемых при общении людей. Как уже отмечалось ранее, эти закономерности играют большую роль в криптоанализе. В частности, они используются при построении формализованных критериев на открытый текст, позволяющих применять методы матема-
48