расшифрования 32-Р отличается от цикла порядком использования 32-битовых элементов ключа. В цикле 32-Р этот порядок следующий: K0, …, K7, K7, …, K0, K7, …, K0, K7, …, K0.

Ниже приведено описание двух поточных режимов работы криптографического алгоритма ГОСТ 28147-89, а именно: гаммирование и гаммирование с обратной связью.

Гаммирование

Криптосхема, реализующая алгоритм зашифрования в режиме гаммирования, имеет вид,

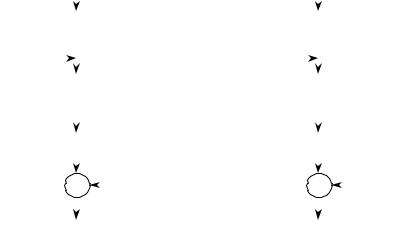
Рис. 2.32. Схема алгоритма зашифрования (а) и расшифрования (б) в режиме гаммирования

Открытые данные, разбитые на 64-разрядные блоки Тоi, зашифровываются в режиме гаммирования путем поразрядного суммирования по модулю 2 с гаммой шифра Гш, которая вырабатывается блоками по 64 бита Гшi, i = 1, …, m. m определяется объемом шифруемых данных. Число двоичных разрядов в блоке Тоm может быть меньше 64, при этом неиспользованная для зашифрования часть гаммы шифра из блока Гшm отбрасывается.

Для инициализации процесса генерации гаммы используется 64-разрядная двоичная последовательность (синхропосылка) S. К синхропосылке применяется цикл зашифрования 32-З. Результат шифрования N разбивается на две части: старшую (N2) и младшую (N1). Значение N2 суммируется по модулю (232 – 1) с 32-разрядной константой C1 = 0101010416. Значение N1 суммируется по модулю 232 с 32-разрядной константой C2 = 0101010116. К полученному значению N применяется цикл зашифрования 32-З. Полученное в результате зашифрования значение N образует первый 64-разрядный блок гаммы шифра Гш1, который суммируется поразрядно по модулю 2 с первым 64-разрядным блоком открытых данных То1. В результате суммирования получается 64-разрядный блок зашифрованных данных Тш1. Для

201

получения следующего 64-разрядного блока гаммы шифра Гш2 старшая часть N2 значения N суммируется по модулю (232 – 1) с константой C1, а младшая часть N1 суммируется по модулю 232 с константой C2. К полученному значению применяется цикл зашифрования 32-З. Полученное в результате зашифрования значение N образует второй 64-разрядный блок гаммы шифра Гш2, который суммируется поразрядно по модулю 2 со вторым блоком открытых данных То2. Аналогично вырабатываются блоки гаммы шифра Гш3, Гш4, …, Гшm и зашифровываются блоки открытых данных То3, То4, …, Тоm. Если длина последнего m-го блока открытых данных Тоm меньше 64 бит, то из последнего m-го блока гаммы шифра Гшm для зашифрования используется только соответствующее число разрядов гаммы шифра, остальные разряды отбрасываются.

Аналогичным образом производится расшифрование в режиме гаммирования (рисунок 2.32б).

Гаммирование с обратной связью

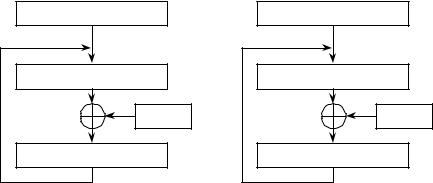
Криптосхема, реализующая алгоритм зашифрования в режиме гаммирования с обратной связью, имеет вид, указанный на рисунке 3а.

Открытые данные, разбитые на 64-разрядные блоки Тоi, зашифровываются в режиме гаммирования с обратной связью путем поразрядного суммирования по модулю 2 с гаммой шифра Гш, которая вырабатывается блоками по 64 бита Гшi, i = 1, …, m. m определяется объемом шифруемых данных. Число двоичных разрядов в блоке Тоm может быть меньше 64.

Рис. 2.33. Схема алгоритма зашифрования (а) и расшифрования (б) в режиме гаммирования с обратной связью

Исходное значение – синхропосылка S зашифровывается с помощью цикла зашифрования 32-З. Полученное в результате зашифрования значение N образует первый 64разрядный блок гаммы шифра Гш1, который суммируется поразрядно по модулю 2 с первым 64-разрядным блоком открытых данных То1. В результате получается 64-разрядный блок зашифрованных данных Тш1.

202