
- •А.М. ГОЛИКОВ
- •Учебное пособие:
- •Томск 2018
- •Учебное пособие
- •История развития криптографии
- •Основные характеристики открытого текста
- •Классификация шифров
- •Шифры перестановки
- •Шифр Хилла
- •Шифры сложной замены
- •Линейный конгруэнтный генератор
- •Регистр сдвига с линейной обратной связью
- •Блочные и поточные системы шифрования
- •Принципы построения блочных шифров
- •Основной шаг криптопреобразования.
- •Базовые циклы криптографических преобразований.
- •Основные режимы шифрования.
- •Простая замена
- •Гаммирование
- •Гаммирование с обратной связью
- •Выработка имитовставки к массиву данных.
- •Американский стандарт шифрования данных DES
- •Основные режимы шифрования
- •Блочный криптоалгоритм RIJNDAEL и стандарт AES
- •Математические предпосылки
- •Сложение
- •Описание криптоалгоритма
- •Раундовое преобразование
- •Атака “Квадрат”
- •Предпосылки
- •Базовая атака “Квадрат” на 4 раунда
- •Добавление пятого раунда в конец базовой атаки “Квадрат”
- •Добавление шестого раунда в начало базовой атаки “Квадрат”
- •Поточные системы шифрования
- •Поточные режимы блочных шифров
- •Строительные блоки поточных шифров
- •Регистры сдвига с обратной связью
- •Регистры сдвига с линейной обратной связью
- •Генераторы на основе LFSR
- •Регистры сдвига с нелинейной обратной связью
- •Регистры сдвига с обратной связью по переносу
- •Поточный шифр HC-128
- •Инициализация
- •Генерация ключевого потока
- •Поточный шифр Rabbit
- •Инициализация
- •Поточный шифр Salsa20
- •Хеш-функция Salsa20
- •Инициализация
- •Функция шифрования Salsa20
- •Поточный шифр SOSEMANUK
- •SERPENT и его производные
- •Инициализация
- •Генерация ключевого потока
- •Поточный шифр F-FCSR-H
- •Генерация ключевого потока
- •Инициализация
- •Поточный шифр Grain-128
- •Генерация ключевого потока
- •Инициализация
- •Поточный шифр MICKEY-128
- •Инициализация
- •Генерация ключевого потока
- •Поточный шифр Trivium
- •Инициализация
- •Генерация ключевого потока
- •Гаммирование
- •Гаммирование с обратной связью
- •Блочный шифр AES в поточном режиме
- •Функция зашифрования
- •Расширение ключа
- •Функция расшифрования
- •Режим обратной связи по шифртексту (CFB)
- •Режим обратной связи по выходу (OFB)
- •Режим счетчика (Counter mode)
- •Методы оценки качества алгоритмов поточного шифрования
- •1. Период
- •2. Криптоанализ шифров
- •3. Линейная сложность
- •4. Исчерпывающий поиск ключа
- •5. Time-memory-data trade-off атака
- •6. Корреляционная атака
- •Быстрая корреляционная атака
- •Алгебраическая атака
- •Атака различением
- •Статистический анализ гаммы шифров
- •Статистические свойства
- •Тестирование
- •Набор статистических тестов НИСТ
- •Частотный тест
- •Частотный тест внутри блока
- •Тест последовательностей
- •Тест наибольших последовательностей единиц в блоке
- •Тест рангов двоичных матриц
- •Спектральный тест
- •Тест сравнения непересекающихся шаблонов
- •Тест сравнения пересекающихся шаблонов
- •Тест сжатия алгоритмом Зива-Лемпела
- •Тест линейной сложности
- •Тест серий
- •Энтропийный тест
- •Тест совокупных сумм
- •Тест случайных отклонений
- •Вариант теста случайных отклонений
- •Анализ результатов тестирования
- •Исследование производительности шифров
- •Rabbit
- •Salsa20/12
- •Salsa20/12
- •Sosemanuk
- •Выводы
- •Цель работы Изучить криптографический стандарт шифрования ГОСТ 28147-89 и его особенности, познакомиться с различными режимами блочного шифрования.
- •Порядок выполнения работы
- •Контрольные вопросы
- •Интерфейс учебно-программного комплекса
- •Главное окно
- •Пункт меню “Файл”
- •Пункт меню “AES”
- •Режимы ECB, CBC, CFB, OFB
- •Режим ECB (Electronic Code Book – режим электронной кодовой книги)
- •Режим CBC (Ciphertext Block Chaining – режим сцепления блоков шифротекста)
- •Режим CFB (Ciphertext Feedback – обратная связь по шифротексту)
- •Режим OFB (Output Feedback – режим обратной связи по выходу)
- •Описание алгоритма
- •Безопасность
- •Программная реализация
- •Заключение
- •Общее описание лабораторной работы
- •Общий вид окна учебной программы
- •Требования к размещению файлов
- •Необходимые знания
- •Загрузка варианта
- •Выбор вероятных составляющих
- •Нахождение вероятной части ключа
- •Определение положения отводов
- •Поиск начального заполнения
- •Получение гаммы
- •Получение открытого текста
- •Отчет о проделанной работе
- •Сообщения выдаваемые в процессе работы
- •Сообщения об ошибках
- •Сообщения-вопросы
- •Критические ошибки
- •Пример
- •Асимметричные криптосистемы [8 -14]
- •Предпосылки появления асимметричных криптосистем
- •Обобщенная схема асимметричной крипосистемы
- •Алгебраическая обобщенная модель шифра
- •Односторонние функции
- •Факторизация
- •Дискретный логарифм
- •Криптосистема RSA
- •Основные определения и теоремы
- •Алгоpитм RSA
- •Процедуры шифрования и расшифрования в криптосистеме RSA
- •Криптосистема Эль-Гамаля
- •Комбинированный метод шифрования
- •Метод экспоненциального ключевого обмена Диффи-Хеллмана
- •Алгоритмы практической реализации криптосистем с открытым ключом
- •Возведение в степень по модулю m
- •Алгоритм Евклида вычисления НОД
- •Вычисление обратных величин в кольце целых чисел
- •Генерация простых чисел
- •Атаки на алгоритм RSA
- •Практическая часть
- •Лабораторная работа 1
- •Ход работы
Функция шифрования Salsa20
Пусть k – это 32или 16-байтовый секретный ключ, iv – 8-байтовый вектор инициализации, m – открытый текст. Тогда шифрование последовательности m шифром Salsa20 с помощью вектор инициализации iv на ключе k, обозначается Salsa20k(iv) m – шифрованный текст. Либо m может быть шифрованным текстом, в случае, когда Salsa20k(iv)m является исходным открытым текстом.
Поточный шифр SOSEMANUK
Sosemanuk – синхронный поточный шифр [6]. Шифр Sosemanuk использует принципы базовой конструкции поточного шифра SN),ключи).ВOW 2.0 преобразования блочного шифра SERPEN),ключи).ВT. Поэтому разработчики решили, что название этого шифра должно относиться и к SERPEN),ключи).ВT и к SN),ключи).ВOW. Однако, известно, что снежных змей не существуют, т.к. змеи либо впадают в спячку, либо перемещаются в более теплые страны на зимы. С другой стороны Sosemanuk – популярный спорт, в который играют восточные канадские племена. Он состоит в броске деревянной палки по сугробу как можно дальше. Его название на языке Cree означает snowsnake, так как палка на снегу похожа на змею. Kwakweco-cime win – вариант той же самой игры, но для названия шифра не походит.
Sosemanuk – синхронный поточный шифр, ориентированный на программную реализацию. Размер ключа варьируется между 128 и 256 битами. Утверждается, что при любой длине ключа достигается 128-битная безопасность. Sosemanuk стремится улучшить SN),ключи).ВOW 2.0 в двух отношениях. Во-первых, в Sosemanuk избегаются некоторые свойства структуры, которые могут проявиться как потенциальные слабости, даже если шифр SN),ключи).ВOW 2.0 с 128-битным ключом сопротивляется всем известным нападениям. Во-вторых, эффективность улучшена относительно нескольких архитектур, уменьшением размера внутреннего состояния, таким образом допускается более прямое отображение данных относительно регистров процессора. Sosemanuk также требует меньшего количества статических данных; соответственно более низкого использования кэша данных, что приводит к лучшей работе на некоторых архитектурах. Другое достоинство Sosemanuk – то, что его процедура установки ключа основана на сокращенной версии блочного шифра SERPEN),ключи).ВT, улучшая классические процедуры инициализации и с точки зрения эффективности и с точки зрения безопасности.
SERPENT и его производные
SERPEN),ключи).ВT – блочный шифр, предложенный в качестве AES кандидата. SERPEN),ключи).ВT работает с 128-битовыми блоками, которые разбиваются на четыре 32-разрядных слова, а
184
затем объединяются в так называемом “секционном” (“bitslice”) режиме. Таким образом SERPEN),ключи).ВT может быть определен как шифр, работающий с четверкой 32-битовых слов. Мы нумеруем входные и выходные четверки SERPEN),ключи).ВT’а от 0 до 3, и пишем им в порядке: (Y3, Y2, Y1, Y0). Y0 – самое младшее слово, содержащее младшие разряды 32-ух 4-битовых входных данных для S-блоков SERPEN),ключи).ВT’а. После того как выходной поток SERPEN),ключи).ВT’а записывается в 16 байтов, в значения Yi записываются в соответствии со следующим условным обозначением littleendian (вначале самый младший байт), и сначала выводится Y0, затем Y1, и так далее.
Из SERPEN),ключи).ВT разработчики определили два примитива по имени Serpent1 и Serpent24. Циклы SERPEN),ключи).ВT’а состоят из:
добавления подключа поразрядным исключающим или (XOR);
применения s-блока, которое заключается в ряде поразрядных комбинаций между четырьмя обрабатываемыми 32-битовыми словами, в секционном режиме (bitslice mode);
линейного биективного преобразования, которое равнозначно нескольким XOR’ам, сдвигам и циклическим сдвигам в секционном режиме (bitslice mode).
Serpent1 – один раунд шифра SERPEN),ключи).ВT, без добавления ключа и линейного преобразования. SERPEN),ключи).ВT использует восемь различных S-блоков, пронумерованных от S0 до S7, рассчитанных на 4-битовые слова. Мы определяем Serpent1 как применение S2, в секционном режиме (bitslice mode). Это третий S-блоковый уровень шифра SERPEN),ключи).ВT. Serpent1 использует в качестве входных данных четыре 32-битовых слова, и вырабатывает четыре 32-битовых слова в качестве выхода.
Serpent24 – это SERPEN),ключи).ВT, сокращенный до 24 раундов, вместо полной 32-х раундовой версии SERPEN),ключи).ВT. Serpent24 соответствует первым 24 раундам шифра SERPEN),ключи).ВT, причем последний (24-й) раунд полный – с линейным преобразованием и XOR’ом с 25-ым подключом. Другими словами, 24-ый раунд Serpent24 эквивалентен тридцать второму раунду шифра SERPEN),ключи).ВT, за исключением того, что содержит линейное преобразование и использует 24-ый и 25-ый подключи (32-ый и 33-ий подключи в SERPEN),ключи).ВT). Соответствующее уравнение последнего раунда приведено в [32_Serpent]
|
|
|
|
|
|
|
|
X L S 23 |
|
|
|||
R23 |
X K 23 |
|
K 24 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Serpent24 использует только 25 128-битовых подключей, которые являются первыми 25 подключами, производящимися в соответствии со схемой разворачивания ключа шифра
185
SERPEN),ключи).ВT. В Sosemanuk Serpent24 используется на этапе инициализации, только в режиме шифрования. При расшифровании не используется.
Инициализация
Процесс инициализации Sosemanuk разбит на два шага:
схема разворачивания ключа, которая подвергает обработке секретный ключ, но не зависит от вектора инициализации IV;
добавление вектора инициализации IV, которое использует выход схемы разворачивания ключа и вектор IV.
Таким образом, инициализируется внутреннее состояние поточного шифра.
Установка ключа соответствует схеме разворачивания ключа в Serpent24, которая производит 25 128-битовых подключей, как 100 32-битовых слова. Эти 25 128-битовых подключей идентичны первым 25 128-битовым подключам, производящимся в соответствии с простой схемой разворачивания ключа в SERPEN),ключи).ВT.
SERPEN),ключи).ВT допускает любую длину ключа длину от 1 до 256 битов; следовательно, Sosemanuk может работать с точно такими же ключами. Однако, так как Sosemanuk стремится к 128-битовой безопасности, длина его ключа должна быть по крайней мере 128 битов. Поэтому, 128 битов – стандартная длина ключа. Поддерживается любая длина ключа от 128 битов до 256 битов. Но, уровень безопасности все же соответствует 128-битовой безопасности. Другими словами, использование более длинного секретного ключа не гарантирует обеспечение уровня безопасности, обычно ожидаемого от такого ключа.
Вектор IV является 128-битовым значением. Используется в качестве входа для блочного шифра Serpent24, инициализированный в соответствии со схемой разворачивания ключа. Serpent24 состоит из 24 раундов, используются выходы 12-го, 18-го и 24-го раундов. Мы обозначим эти выоды следующим образом:
(Y312, Y212, Y112, Y012) – выход 12-ого раунда;
(Y318, Y218, Y118, Y018) – выход 18-ого раунда;
(Y324, Y224, Y124, Y024) – выход 24-ого раунда.
Выход каждого раунда состоит из четырех 32-битовых слов, берущихся только после линейного преобразования, за исключением 24-ого раунда, для которого выход берется только после добавления 25-ого подключа.
Эти значения используются для инициализации внутреннего состояния Sosemanuk’а со следующими значениями:
(s7, s8, s9, s10) = (Y312, Y212, Y112, Y012) (s5, s6) = (Y118, Y318)
186
(s1, s2, s3, s4) = (Y324, Y224, Y124, Y024)
R10 = Y018
R20 = Y218
Генерация ключевого потока
Для формирования выходных значений zt используется конечный автомат (FSM, Finite State Machine) и функция Serpent1.
Конечный автомат (FSM) – компонент с 64 битами памяти, аналогичный двум 32битовым регистрам R1 и R2. В каждом шаге FSM берет в качестве входных данных некоторые слова из состояния LFSR; обновляет биты памяти и производит 32-битовый выход. FSM оперирует состоянием LFSR в моменты времени t 1 следующим образом:
FSMt: (R1t–1, R2t–1, st+1, st+8, st+9) (R1t, R2t, ft) где
R1t = (R2t–1 + mux(lsb(R1t–1), st+1, st+1 st+8)) mod 232
R2t = Trans(R1t–1)
ft = (st+9 + R1t mod 232) R2t где lsb(x) – младший бит x,
mux(c, x, y) равен x если c = 0, или y если c = 1.
Внутренняя переходная функция Trans над полем F232 определяется как Trans(z) = (M z mod 232)<<<7
где М – постоянное значение, равное 0x54655307 (шестнадцатеричное выражение первых десяти десятичных чисел π).
Выходы конечного автомата FSM группируются по четыре, и Serpent1 применяется к каждой группе; затем результат объединяется XOR’ом с соответствующими отбрасываемыми значениями LFSR, для производства выходных значений zt:
(zt+3, zt+2, zt+1, zt) = Serpent1(ft+3, ft+2, ft+1, ft) (st+3, st+2, st+1, st)
Четыре последовательных раунда Sosemanuk изображены на рисунке 2.26
187
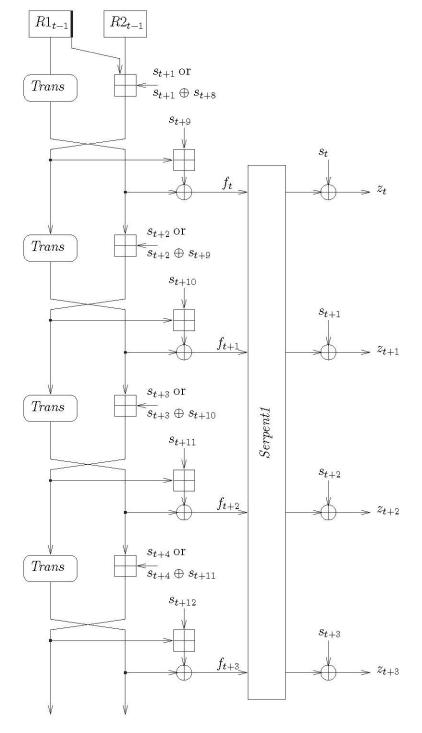
Рис. 2.26. Выходное преобразование четырех последовательных раундов Sosemanuk Шифр Sosemanuk объединяет FSM и LFSR для производства выходных значений zt.
Время t = 0 определяет внутреннее состояние после инициализации; первое выходное значение – z1. На рисунке 3 представлено описание шифра Sosemanuk.
188
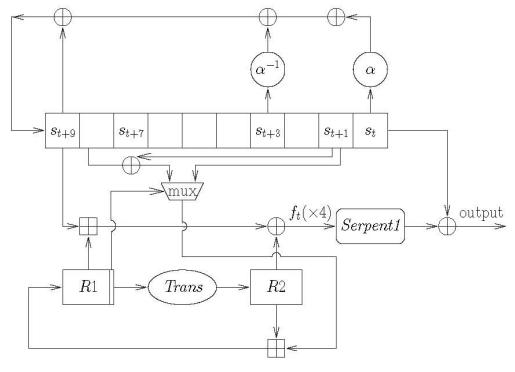
Рис. 2.27. Описание шифра Sosemanuk
Вмоменты времени t 1 выполняются следующие операции:
обновляется FSM: из R1t−1, R2t−1, st+1, st+8 и st+9 вычисляются R1t, R2t и промежуточные значения ft.
обновляется LFSR: из st, st+3 и st+9 вычисляется st+10. Значение st передается внутреннему буферу, LFSR сдвигается.
Каждые четыре шага, из накопленных значений ft, ft+1, ft+2, ft+3 и st, st+1, st+2, st+3 производятся четыре выходных значения zt, zt+1, zt+2, и zt+3. Таким образом, Sosemanuk производит 32битовые значения.
Соответственно первые четыре итерации Sosemanuk’а следующие:
Начальное состояние LFSR содержит значения s1, …, s10; значение s0 не определено. Начальное состояние FSM содержит R10 и R20.
В течение первого шага из R10, R20, s2, s9 и s10 вычисляются R11, R21 и f1.
Первый шаг производит промежуточные значения s1 и f1, сохраняемые в
буфере.
В течение первого шага, вычисляется слово обратной связи s11 из s10, s4 и s1, обновляется внутреннее состояние LFSR, что приводит к новому состоянию, формируемое из s2, …, s11.
Первые четыре выходные значения – z1, z2, z3 и z4, вычисляются,
используя однократное применение Serpent1’а к (f4, f3, f2, f1), выход которого
объединяется с (s4, s3, s2, s1) при помощи XOR. 189
