вычисление имитовставки для заданного открытого массива информации;
подбор открытых данных под заданную имитовставку;
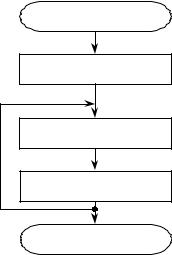
Схема алгоритма выработки имитовставки приведена на рисунке 2.7.
Начало (Tо)
S = 0
i = 1 .. n
S = Ц16-З (S Т iо )
И = (s0, s1, … , sr–1)
Конец (И)
Рис. 2.7. Алгоритм выработки имитовставки для массива данных
В качестве имитовставки берется часть блока, полученного на выходе, обычно 32 его младших бита. При выборе размера имитовставки надо принимать во внимание, что вероятность успешного навязывания ложных данных равна величине 2–|И| на одну попытку подбора. При использовании имитовставки размером 32 бита эта вероятность равна 2–32 0,23 10–9.
Американский стандарт шифрования данных DES
Стандарт шифрования данных DES (Data Encryption Standard) опубликован Национальным бюро стандартов США в 1977 г. В 1980 г. этот алгоритм был принят Национальным институтом стандартов и технологий США (НИСТ) в качестве стандарта шифрования данных для защиты от несанкционированного доступа к важной, но несекретной информации в государственных и коммерческих организациях США.
Основные достоинства алгоритма DES:
простота ключевой системы (используется только один ключ длиной 56
бит);
относительная простота алгоритма обеспечивает высокую скорость аппаратной и программной реализации;
достаточно высокая криптографическая стойкость алгоритма шифрования.
135
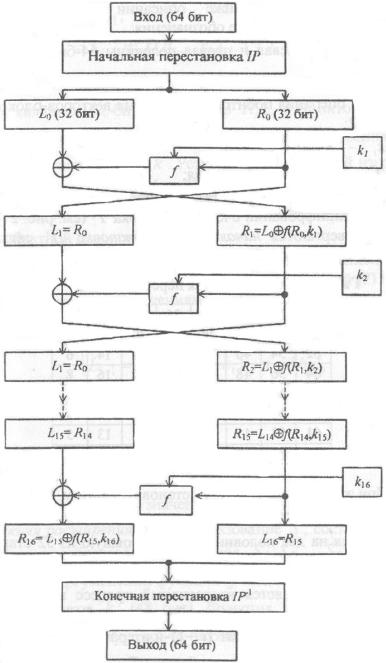
Алгоритм DES использует комбинацию подстановок и перестановок. DES осуществляет шифрование 64-битовых блоков данных с помощью 56-битового ключа k, в котором значащими являются 56 бит (остальные 8 бит – проверочные биты для контроля на четность). Дешифрование в DES является операцией, обратной шифрованию, и выполняется путем повторения операций шифрования в обратной последовательности. Структура алгоритма DES изображена на рисунке 2.8.
Li, Ri – левая и правая половины 64-битового блока;
– операция побитового сложения блоков по модулю 2 (XOR); ki – 48-битовые ключи, получаемые из исходного ключа k;
136
f – функция шифрования;
IP – начальная перестановка степени 64.
Рис. 2.8. Структура алгоритма DES
Процесс шифрования состоит в начальной перестановке битов 64-битового входного блока, шестнадцати циклах шифрования и, наконец, конечной перестановке битов.
Отметим, что все приводимые ниже таблицы являются стандартными и должны использоваться при реализации алгоритма DES в неизменном виде. Все перестановки и коды в таблицах подобраны разработчиками таким образом, чтобы максимально затруднить процесс вскрытия шифра путем подбора ключа.
При зашифровании очередного блока Т (рисунок 4.8) его биты подвергаются начальной перестановке IP согласно приводимой таблице 2.1.
|
|
|
|
|
Таблица 2.1. Начальная перестановка IP |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
5 |
5 |
4 |
3 |
2 |
1 |
1 |
2 |
||
8 |
0 |
2 |
4 |
6 |
8 |
|
0 |
|
||
|
|
|
|
|||||||
|
6 |
5 |
4 |
3 |
2 |
2 |
1 |
4 |
||
0 |
2 |
4 |
6 |
8 |
0 |
|
2 |
|
||
|
|
|
|
|||||||
|
6 |
5 |
4 |
3 |
3 |
2 |
1 |
6 |
||
2 |
4 |
6 |
8 |
0 |
2 |
|
4 |
|
||
|
|
|
|
|||||||
|
6 |
5 |
4 |
4 |
3 |
2 |
1 |
8 |
||
4 |
6 |
8 |
0 |
2 |
4 |
|
6 |
|
||
|
|
|
|
|||||||
|
5 |
4 |
4 |
3 |
2 |
1 |
9 |
1 |
||
7 |
9 |
1 |
3 |
5 |
7 |
|
||||
|
|
|
|
|
||||||
|
5 |
5 |
4 |
3 |
2 |
1 |
1 |
3 |
||
9 |
1 |
3 |
5 |
7 |
9 |
|
1 |
|
||
|
|
|
|
|||||||
|
6 |
5 |
4 |
3 |
2 |
2 |
1 |
5 |
||
1 |
3 |
5 |
7 |
9 |
1 |
|
3 |
|
||
|
|
|
|
|||||||
|
6 |
5 |
4 |
3 |
3 |
2 |
1 |
7 |
||
3 |
5 |
7 |
9 |
1 |
3 |
|
5 |
|
||
|
|
|
|
|||||||
При этом бит 58 блока T становится битом 1, бит 50 – битом 2 и т. д. Полученный после перестановки блок IP(T) разделяется на две половины: L0, состоящую из 32 старших бит, и R0, состоящую из 32 младших бит.
Затем выполняется итеративный процесс шифрования, состоящий из 16 циклов преобразования Фейстеля. Пусть Ti–1 = Li–1Ri–1 – результат (i – 1)-й итерации.
Тогда результат i-й итерации Ti = LiRi определяется формулами 137
Li Ri 1 , |
(6) |
Ri Li 1 fi Ri 1 , ki , i 1,16. |
Функция f называется функцией шифрования. Ее аргументами являются 32-битовый вектор Ri–1 и 48-битовый ключ ki, который является результатом преобразования 56-битового ключа шифра k. Результатом последней итерации является блок T16 = L16R16. По окончании шифрования осуществляется восстановление позиций битов применением к T16 обратной перестановки IP–1.
При расшифровании данных все действия выполняются в обратном порядке, при этом вместо соотношений (4.2) следует пользоваться соотношениями
Ri 1 Li ,
Li 1 Ri fi Li , ki , i 16,1,
пользуясь которыми можно "спуститься" от L16 и R16 к R0 и L0.
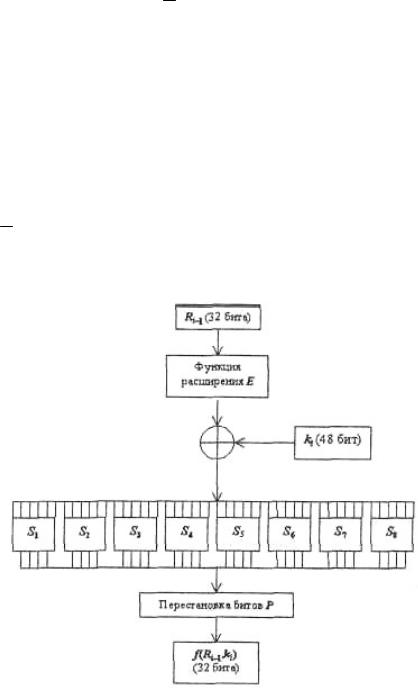
Схема вычисления значения функции шифрования f(Ri–1, ki) изображена на рисунке 2.9.
Рис. 2.9. Схема вычисления функции шифрования f
Для вычисления значения функции f используются:
функция расширения Е;
преобразование S, составленное из восьми преобразований S-тест,блоков S1,
S2, …, S8;
перестановка Р.
Аргументами функции f являются вектор Ri–1 (32 бита) и вектор ki (48 бит). Функция Е
"расширяет" 32-битный вектор Ri–1 до 48-битного вектора E(Ri–1) путем дублирования 138
некоторых битов вектора Ri–1, при этом порядок следования битов в E(Ri–1) указан в таблице 2.2.
|
|
|
|
Таблица 2.2. Функция расширения E |
|||
|
|
|
|
|
|
|
|
32 |
1 |
2 |
3 |
|
4 |
5 |
|
4 |
5 |
6 |
7 |
|
8 |
9 |
|
8 |
9 |
10 |
11 |
|
12 |
13 |
|
12 |
13 |
14 |
15 |
|
16 |
17 |
|
16 |
17 |
18 |
19 |
|
20 |
21 |
|
20 |
21 |
22 |
23 |
|
24 |
25 |
|
24 |
25 |
26 |
27 |
|
28 |
29 |
|
28 |
29 |
30 |
31 |
|
32 |
1 |
|
Первые три бита в E(Ri–1) – это соответственно биты 32, 1 и 2 вектора Ri–1, а последние три бита – это соответственно биты 31, 32, 1 вектора Ri–1.
Полученный результат складывается побитно по модулю 2 с текущим значением ключа ki и затем представляется в виде восьми последовательных 6-битовых блоков B1, B2, …, B8:
E(Ri–1) ki = B1 … B8.
Далее каждый из блоков Bj трансформируется в 4-битовый блок B j с помощью подходящей таблицы S-блока Sj, список которых приведен в таблице 3.
Таблица 2.3. Функция преобразования S
139
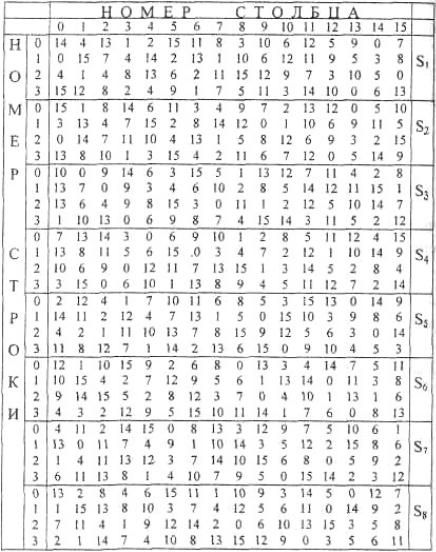
Преобразование блока Bj и B j осуществляется следующим образом. Пусть, например, В2 равен 111010. Первый и последний разряды B2 являются двоичной записью числа a, 0 a 3. Аналогично средние 4 разряда представляют число b, 0 b 15. В нашем примере a = 2, b = 13.
Строки и столбцы таблицы S2 пронумерованы числами a и b. Таким образом, пара (a, b) однозначно определяет число, находящееся на пересечении строки с номером a и столбца с номером b. В данном случае это число равно 3. Записывая его в двоичной форме, получаем B 2, равный 0011.
Значение f(Ri–1, ki) теперь получается применением перестановки битов P, заданной таблицей к результирующему 32-битовому блоку B 1, B 2, …, B 8.
Таблица 2.4. Функция P перестановки битов
140
16 |
7 |
20 |
21 |
29 |
12 |
28 |
17 |
1 |
15 |
23 |
26 |
5 |
18 |
31 |
10 |
2 |
8 |
24 |
14 |
32 |
27 |
3 |
9 |
19 |
13 |
30 |
6 |
22 |
11 |
4 |
25 |
На каждой итерации используется текущее значение ключа ki (48 бит), получаемое из исходного ключа k следующим образом.
Сначала пользователи выбирают сам ключ k, содержащий 56 случайных значащих битов. Восемь битов, находящихся в позициях 8,16,...,64, добавляются в ключ таким образом, чтобы каждый байт содержал нечетное число единиц. Это используется для обнаружения ошибок при обмене и хранении ключей. Значащие 56 бит ключа подвергаются перестановке, приведенной в таблице 2.5.
Таблица 2.5. Функция первоначальной подготовки ключа
57 |
|
4 |
|
4 |
|
3 |
2 |
1 |
9 |
9 |
|
1 |
|
3 |
5 |
7 |
|
||
|
|
|
|
|
|||||
1 |
|
5 |
|
5 |
|
4 |
3 |
2 |
18 |
8 |
|
0 |
|
2 |
4 |
6 |
|
||
|
|
|
|
|
|||||
10 |
|
2 |
|
5 |
|
5 |
4 |
3 |
27 |
|
9 |
|
1 |
3 |
5 |
|
|||
19 |
|
1 |
|
3 |
|
6 |
5 |
4 |
36 |
1 |
|
|
0 |
2 |
4 |
|
|||
63 |
|
5 |
|
4 |
|
3 |
3 |
2 |
15 |
5 |
|
7 |
|
9 |
1 |
3 |
|
||
|
|
|
|
|
|||||
7 |
|
6 |
|
5 |
|
4 |
3 |
3 |
22 |
2 |
|
4 |
|
6 |
8 |
0 |
|
||
|
|
|
|
|
|||||
14 |
|
6 |
|
6 |
|
5 |
4 |
3 |
29 |
|
1 |
|
3 |
5 |
7 |
|
|||
21 |
|
1 |
|
5 |
|
2 |
2 |
1 |
4 |
3 |
|
|
8 |
0 |
2 |
|
Эта перестановка определяется двумя блоками C0 и D0 по 28 бит в каждом (они занимают соответственно верхнюю и нижнюю половины таблицы). Так, первые три бита в C0 есть соответственно 57, 49, 41 биты ключа. Затем индуктивно определяются блоки Ci и Di = 1,16
.
141