Защита информации в радиоэлектронных системах передачи информации

Лабораторная работа. 4. Скремблирования аудиосигнала

с использованием Вейвлет преобразования

Запись аудио сигнала

Для записи аудиосигнала использовались встроенные средства программы MatLab.

Изначально для записи голосового сообщения необходимо знать состояние системы и ID

подключенных устройств.

Воспользовавшись следующим программным кодом:

devinfo = audiodevinfo;

disp('Input devices');

for i = 1 : size(devinfo.input, 2) devinfo.input(i) end

disp('Output devices');

for i = 1 : size(devinfo.output, 2) devinfo.output(i) end

Получаем сведения о системе представленные на рисунке 1.

Рис.1. Сведения о системе

181

Далее зная параметры системы возможно произвести запись аудиосигнала с

помощью встроенных в MatLab функций. Для этого был написан следующий

программный код:

Fs = 8000; % Количество отсчетов nBits = 16; % Битов на отсчет nChannels = 2; % Количество каналов

deviceID = 1; % ID микрофона подключенного к компьютьеру recObj = audiorecorder(Fs, nBits, nChannels, deviceID); get(recObj)

nSeconds = 10;

%Запись голоса и графическое представление записанного сигнала

%Запись в течении nSeconds секудн disp('Start

speaking.') recordblocking(recObj, nSeconds); disp('End of Recording.');

% Проигрышь записанного голосового собщения. play(recObj);

%Получение аудиоданных myRecording = getaudiodata(recObj);

%Графическое представление plot(myRecording); %Сохранение каналов x1=myRecording(:,1);

x2=myRecording(:,2); save Record1; save Chanel1 x1; save Chanel2

x2;

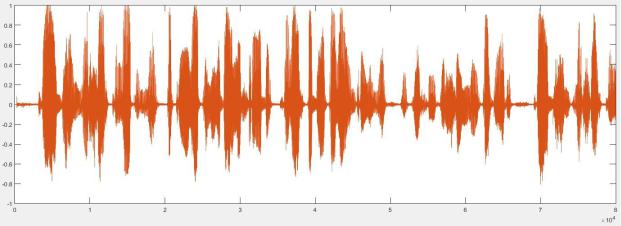
Врезультате выполнения программы на экран будет выведен график отображающий записанные аудиоданные.

Рис.2. Записанные аудиоданные

182

Быстрое вейвлет преобразование сигнала

Благодаря своим частотно-временным свойствам вейвлетпреобразование предоставляет широкий спектр возможностей для работы с различного рода сигналами.

Помимо классического применения в виде фильтрации и сжатия, вейвлет преобразования являются удобным аппаратом для работы с сигналами в области информационной безопасности. Например, вейвлет преобразование достаточно часто упоминается в различных разделах стеганографии. Так же на основе БВП возможно выполнить сокрытие аудио информации одновременно во временной и частотной области.

Для выполнения быстрого вейвлет-преобразования был разработан следующий

код:

%Загружаем файл с одним из каналов load('Chanel1.mat');

%имя вейвлета wname='sym4'; lev=4;

x=x1';

[dec,struct]=wavedec(x1,lev,wname);

%Вектор dec содержит столбец данных состоящий последовательно приписанных

%уровенй разложения, struct содержит информацию о кол-ве элементов в

%разложении для выделения определенного разложения из dec

%Извлечение коэффициентов разложения sa4

= appcoef (dec, struct, wname,4); sd4= detcoef (dec, struct, 4);

sd3= detcoef (dec, struct, 3); sd2= detcoef (dec, struct, 2); sd1= detcoef (dec, struct, 1);

% Графическая поддержка subplot (711)

plot (x1), title ('Исходный сигнал') subplot (712)

plot (sd1), ylabel ('sd1') subplot (713)

plot (sd2), ylabel ('sd2') subplot (714)

plot (sd3), ylabel ('sd3') subplot (715)

plot (sd4), ylabel ('sd4') subplot

(716)

plot (sa4), ylabel ('sa3')

x2 = waverec (dec, struct, wname); % Рисуем восстановленный сигнал subplot (717);

plot (x2), title ('Восстановленый сигнал'); save wav_dec;

183

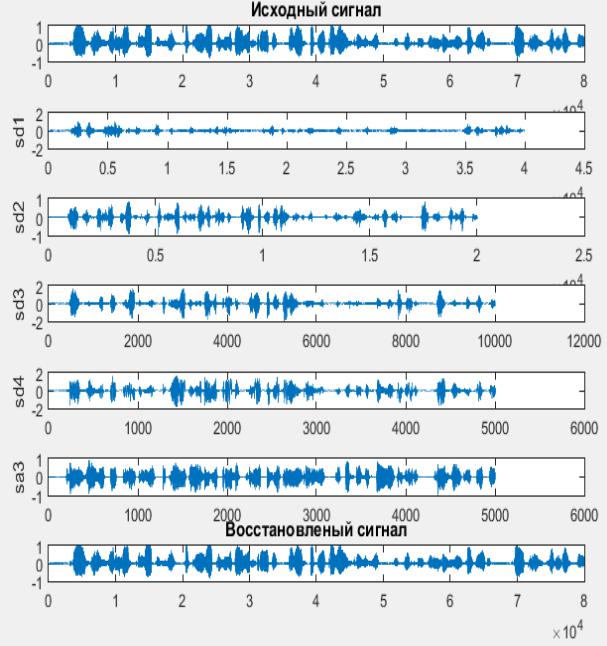
На рисунке 3. изображено разложение и

восстановление аудиосигнала при помощи БВП с использованием

симлета 4.

Рис.3. Быстрое вейвлет преобразование примененное к аудиосигналу

Скремблирование сигнала

Для того чтобы скрыть информацию в аудиосигнале, достаточно перемешать коэффициенты различных уровней разложения между собой по определенному алгоритму. Благодаря свойствам вейвлет-спектра подобное воздействие на вейвлет коэффициенты приведет к изменению сигнала как в частотной, так и во временной области.

184

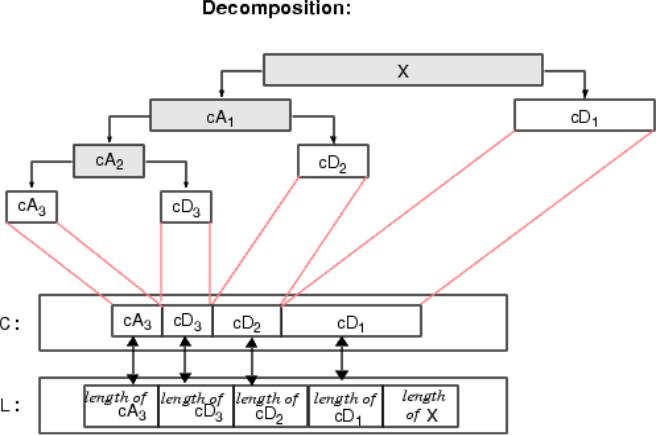
В программе MatLab декомпозиция сигнала представлена в следующем виде

Рис.4. Результат выполнения БВП в MatLab

Как видно из рисунка на выходе имеется вектор вейвлет коэффициентов

составленный из коэффициентов на всех уровнях, последовательным приписыванием

каждого уровня к предыдущему начиная с минимального. Данный вид

представления позволяет выполнить перемежение вейвлет коэффициентов простым

переобазначением индексов массива.

В дальнейшем восстановив из перемешанного спектра сигнал, получается

заскремблированные аудиоданные как в частотной так и во временной области.

Для перемежения коэффициентов спектра быстрого вейвлет преобразования и

последующего восстановления скремблированного сигнала был разработан

следующий код:

%загрузка коэффициентов load('wav_dec.mat');

for i=1:1:10000

new_dec(i)=dec(40000+i-1);% от 40000 до 50000 /10000 new_dec(10000+i)=dec(60000+i-1); % от 60000 до 70000 /20000 new_dec(20000+i)=dec(i); % от 0 до 10000 /30000 new_dec(30000+i)=dec(70000+i-1); % от 70000 до 80000 /40000

185

new_dec(40000+i)=dec(10000+i-1); % от 10000 до 20000 /50000 new_dec(50000+i)=dec(30000+i-1); % от 30000 до 40000 /60000 new_dec(60000+i)=dec(20000+i-1); % от 20000 до 30000 /70000 new_dec(70000+i)=dec(50000+i-1); % от 50000 до 60000 /80000 end

for i=80000:1:80026

new_dec(i)=dec(i); % от 50000 до 60000 /80000 end

new_dec=new_d

ec';

save ScrDecomp new_dec;

% Извлечение коэффициентов разложения new_sa4 = appcoef (new_dec, struct, wname,4); new_sd4= detcoef (new_dec, struct, 4); new_sd3= detcoef (new_dec, struct, 3); new_sd2= detcoef (new_dec, struct, 2); new_sd1= detcoef (new_dec, struct, 1);

% Графическая поддержка subplot (711)

plot (x1), title ('Исходный сигнал') subplot (712)

plot (new_sd1), ylabel ('sd1') subplot (713)

plot (new_sd2), ylabel ('sd2') subplot (714)

plot (new_sd3), ylabel ('sd3') subplot (715)

plot (new_sd4), ylabel ('sd4')

subplot (716)

plot (new_sa4), ylabel ('sa3')

scrembl_sign = waverec (new_dec, struct, wname); % Рисуем восстановленный

сигнал subplot (717);

plot (scrembl_sign), title ('Скремблированный сигнал'); save Scr_sig scrembl_sign;

load('Record1.mat'); Voice_sound(:,1)=scrembl_sign(:,1); Voice_sound(:,2)=scrembl_sign(:,1);

player = audioplayer(Voice_sound, Fs, nBits); start = 1;

stop = player.SampleRate * nSeconds;

play(player, [start stop]);

%pause(player)

%resume(player)

При выполнении данного кода были получены следующие результаты:

186

Рис. 5. Разложение на уровне d1

Рис.6. Разложение на уровне d2

Рис.7. Разложение на уровне d3

187

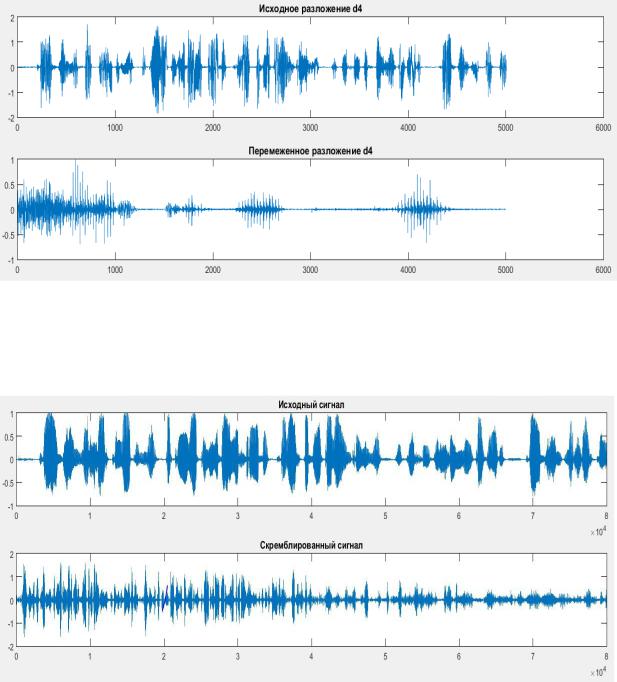
Рис.8. Разложение на уровне d4

При этом из полученный сигнал не похож на исходной в достаточной степени, чтобы говорить о защищенности информации.

Рис. 9. Исходный и заскремблированный сигналы.

Восстановление исходного сигнала

Для восстановления исходного сигнала скремблированный сигнал подвергается быстрому вейвлет преобразованию. Полученные коэффициенты вейвлет-спектра по алгоритму, обратному скремблирующему, перемешиваются, для получения исходного спектра. На основании полученного спектра происходит восстановление сигнала. При должном навыке и практических исследованиях возможно добиться восстановления сигнала без искажений. На рисунке 10

представлен восстановленный сигнал имеющий небольшие искажения в следствии

188

несовершенных алгоритмов перемежения спектра.

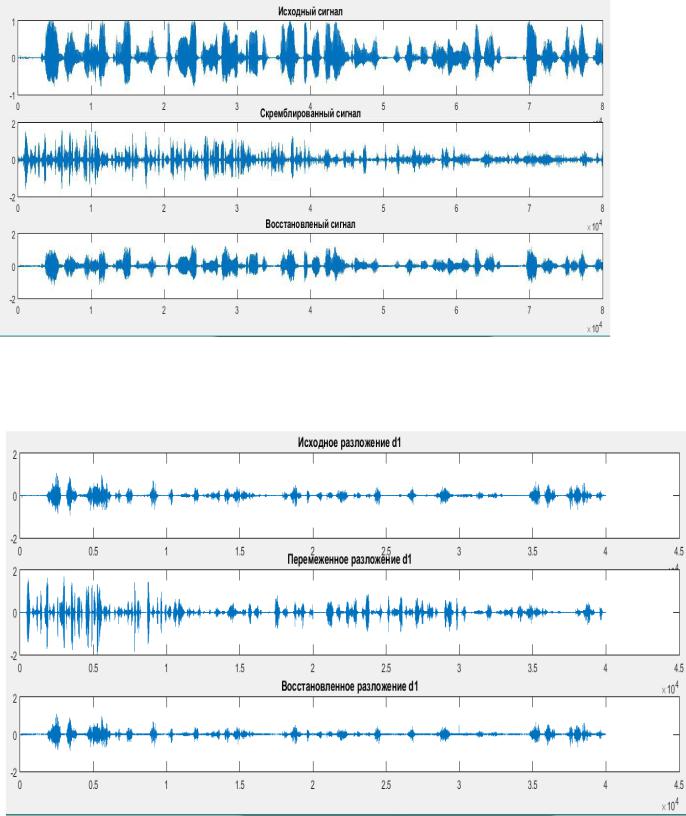
Рис.10. Исходный, заскремблированный и восстановленный сигналы На рисунке 2.11

представлено разложение на уровне d1, как видно восстановленный спектр довольно точно повторяет исходный.

Рис. 11. Исходный, заскремблированный и восстановленный уровни разложения d1

На рисунках 12-14 изображены разложения на уровнях d2, d3 и d4 соответственно.

189

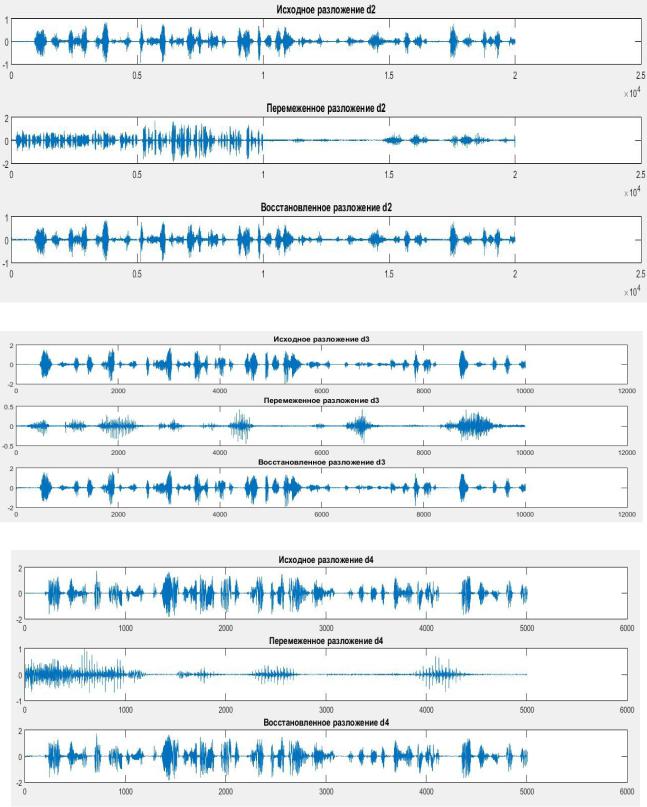
Рис.12. Исходный, заскремблированный и восстановленный уровни разложения d2

Рис. 13. Исходный, скремблированный и восстановленный уровни разложения d3

Рис.14. Исходный, скремблированный и восстановленный уровни разложения d4

В лабораторной работе исследовано скремблирование аудиосигнала с помощью вейвлет преобразования. Установлено, что вейвлет преобразование позволяет выполнить как частотное так и временное скремблирование одновременно,

что повышает крипто стойкость. Восстановленный сигнал в достаточной степени

190