
Электромагнитная совместимость
..pdf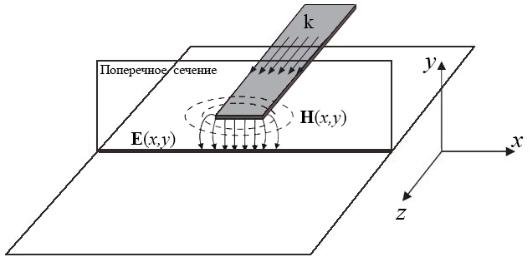
ковые структуры, которые широко используются для создания элементов РЭС: печатных плат, фильтров, средств снижения уровня перекрестных помех или их компенсации, устройств защиты, фазовращателей, антенн, линий задержки, высокоскоростных межсоединений и пр.
Рисунок 1.6 – Общий вид воздушной микрополосковой линии передачи
При квазистатическом подходе электрические характеристики, меняющиеся вдоль отрезков МПЛП длиной dx, описываются матрицами погонных первичных параметров R (Ом/м), L (Гн/м), С (Ф/м) и G (См/м), или кратко RLCG-параметрами. Отдельно отметим, что вычисление (экстракция) этих матриц (в частности, R и С) является важной задачей при проектировании с учетом паразитных параметров выводов интегральных схем, а случайные вариации их параметров в технологическом процессе вынуждают многократно вычислять эти матрицы. Вычисленные матрицы затем используются при решении телеграфных уравнений Хевисайда или производных от них для анализа целостности сигналов, получения временного отклика и других параметров.
В случае неучета потерь в проводниках и диэлектриках, из которых состоит линия передачи, вычисляются только матрицы L и С. Эти потери объясняются неидеальностью материлов, выражающейся частотной зависимостью электрофизических параметров линии (относительных диэлектрической и магнитной
– 41 –
проницаемостей), скин-эффектом (ток высокой частоты протекает преимущественно в тонком поверхностном слое проводника), эффектом близости (притяжение противоположных токов в соседних проводниках) и угловым эффектом (сжатие тока вблизи углов проводника). Таким образом, строгое решение уравнений Максвелла сводится к двум независимым граничным задачам электростатики и магнитостатики, определяющим поведение поперечных электрических и магнитных компонентов поля. При этом решение первой задачи дает матрицы C и G, а второй – L и R. Для экономии вычислительных затрат часто прибегают только к решению электростатической задачи, а из вычисленной матрицы C находят L и затем R. При этом вычисленная матрица L является частотнонезависимой и тем самым лишь приближенной. На практике это приемлемо, например, при проектировании интегральных схем, поскольку частоты сигналов не так высоки и индуктивные эффекты проявляются слабо.
Для пояснения процесса вычислений рассмотрим уравнение Пуассона (дифференциальная форма)
2 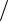 ,
,
где – электростатический потенциал; – объемная плотность заряда. При отсутствии в анализируемой области свободных зарядов данное уравнение сводится к уравнению Лапласа. Для нахождения волнового сопротивления и других параметров одиночной линии передачи с неоднородным диэлектрическим заполнением без потерь необходимо определить погонную емкость с диэлектрическим заполнением С и без него (без границ диэлектрикдиэлектрик) С0. Волновое сопротивление линии передачи без потерь определяется как
Z |
L |
, |
(1.26) |
|
С |
||||
|
|
|
где L – погонная индуктивность; C – погонная емкость. Для нахождения индуктивности можно воспользоваться выражением
L μ0ε0 С01.
– 42 –
При этом фазовая скорость определяется как |
|
||||
u |
1 |
или u с С0 |
с |
, |
(1.27) |
|
|
||||
|
LC |
С |
εreff |
|
|
где с – скорость света в свободном пространстве; |
εreff C C0 – |
||||
эффективная относительная диэлектрическая проницаемость.
Вслучае простых конфигураций линии можно воспользоваться известными аналитическими выражениями [13]. Для сложных МПЛП такие выражения отсутствуют или имеют ограниченную точность и необходимо прибегать к помощи численных методов.
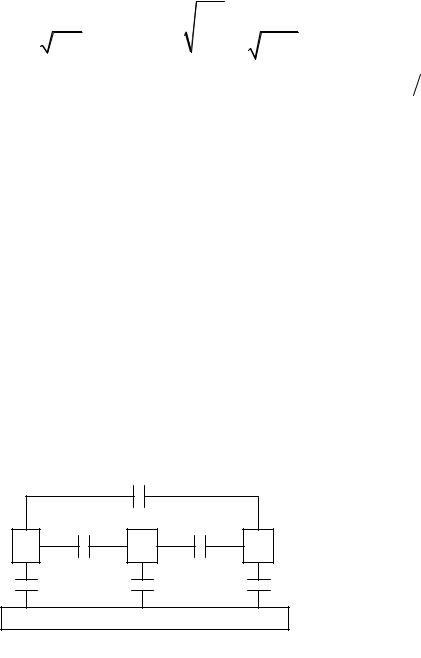
Вобщем случае величины L и С в приведенных выражениях являются матрицами погонных коэффициентов электростатической (C) и электромагнитной (L) индукции [14]. Также матрицу С часто называют емкостной матрицей Максвелла, узловой емкостной матрицей и погонной емкостной матрицей (для краткости далее емкостная матрица). Поясним особенности вычисления емкостной матрицы С на примере трехпроводной линии передачи, поперечное сечение которой приведено на рисунке 1.7.
Рисунок 1.7 – Поперечное сечение трехпроводной линии передачи
Рассмотрим задачу нахождения погонных зарядов Q при известных потенциалах на них [10]. На практике часто потенциал опорного проводника (плоскости земли) устанавливается равным нулю. Разности потенциалов между ним и проводниками обозначим 1, 2 и 3, а между проводниками – 12, 13 и 23. Тогда
QI C1 1 C12 12 C13 13 ,
QII C21 12 C2 2 C23 23 ,
– 43 –

QIII C31 13 C32 23 C3 3.
Перепишем эту систему уравнений в виде
QI C1 1 C12 ( 1 2 ) C13 ( 1 3 )(C1 C12 C13 ) 1 C12 2 C13 3,
QII C21( 2 1) C2 2 C23 ( 2 3 )C21 1 (C2 C21 C23 ) 2 C23 3,
QIII C31( 3 1) C32 ( 3 2 ) C3 3C31 1 C32 2 (C3 C31 C32 ) 3,
или в матричном виде
Q = C ,
где
C11 |
C12 |
C13 |
|
|
|
C22 |
|
|
|
C C21 |
C23 |
|||
|
C32 |
|
|
|
C31 |
C33 |
|
||
C |
C |
C |
C |
|
C |
|
|
|
|
1 |
12 |
13 |
12 |
|
13 |
|
|
|
|
C21 |
C2 C21 C23 |
|
C23 |
|
. |
|
|
|
C |
|
C |
C C C |
|
||
|
|
31 |
32 |
3 |
31 |
32 |
|
|
Коэффициенты Сij называются коэффициентами электростатической индукции – собственными при одинаковых индексах и взаимными при разных индексах. Они имеют размерность погонной емкости [15]. Несмотря на отрицательный знак у внедиагональных элементов матрицы C, емкость между отдельным проводником и плоскостью земли положительна. Тогда матрица L вычисляется как
L μ0ε0 С01.
При учете потерь в проводниках и диэлектриках волновое сопротивление МПЛП описывается комплексной матрицей
Z |
R j L |
|
G j С |
порядка NCOND – число проводников МПЛП, не считая опорного. Для вычисления матрицы G используется та же модель, что и для
– 44 –
матрицы C, с той лишь разницей, что диэлектрическая проницаемость i-го подынтервала заменяется на комплексную с использованием тангенса угла потерь r = r' – j r'' = r'(1 – jtan ) , где tan = r'' / r' ; – удельная проводимость диэлектрика.
Нахождение матрицы R представляет собой сложную задачу. Так, для нетиповых структур часто прибегают к ее измерениям или различного рода упрощениям. Для ее вычисления разработано несколько подходов разной степени сложности, пригодных только для некоторых частотных диапазонов. С точки зрения минимизации вычислительных затрат на вычисление матрицы R выделяется работа [16], где представлено обобщение на случай МПЛП результатов для одиночных линий передачи, использующих правило дифференциальной индуктивности (incremental inductance rule). Рассмотрим ее основные результаты.
В случае одиночной линии передачи потери (омические) в проводнике определяются как
R |
1 |
Rsj |
L |
, |
Rsj πfμρsj , |
|
|
||||
|
μ0 j |
nj |
|
||
где L/ nj – производная индуктивности при небольшой вариации (возмущения) j-й границы поверхности проводника к его центру (сужение проводника); nj – вектор нормали к границе j; Rsj – по-
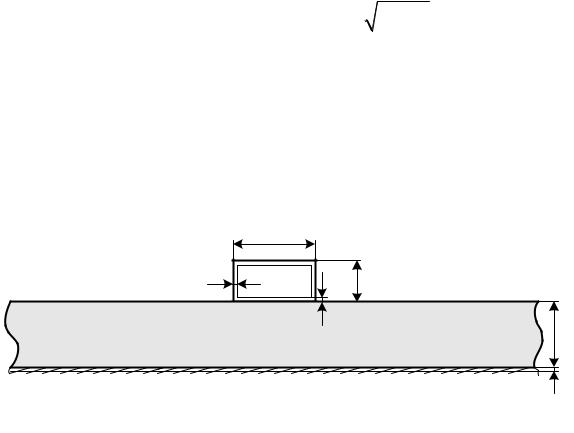
верхностное сопротивление слоя вариации для этой границы (рисунок 1.8); ρsj – удельное сопротивление проводника c границей j.
|
|
|
w |
|
|
w |
t = |
h |
w |
t |
r1=1 |
|
|||||
|
|
|
|
t |
|
r2 |
r2 |
h |
|
h
Рисунок 1.8 – Пояснение вариации границ проводников
Вработе [16] предложено не сужать границы проводников,
анаоборот, расширять, что позволило обобщить данный подход
–45 –
на случай МПЛП и получить более точные результаты. Элементы матрицы R вычисляются как
|
1 |
|
Rsj |
L |
|
||
|
|
|
|
ii , |
если i k; |
||
|
0 |
||||||
|
|
j |
n j |
|
|||
Rik |
1 |
|
Rsj |
Lik |
|
|
|
|
|
, |
иначе. |
||||
|
|
|
|
||||
|
0 |
j |
n j |
|
|||
|
|
||||||
При i = k возмущения применяются к i-му и опорному проводникам, а в противном случае – только к опорным.
Таким образом, особый интерес для минимизации затрат времени на получение всех первичных параметров МПЛП представляет вычисление емкостной матрицы, поскольку, как было показано выше, остальные три матрицы являются ее производными. Поэтому в последующих разделах особое внимание уделяется именно вычислению емкостной матрицы.
Контрольные вопросы и задания
1.Опишите процесс построения математической модели для анализа электромагнитных задач.
2.Запишите уравнения электростатики.
3.В чем различие между уравнениями Лапласа и Пуассона?
3.Как классифицируются дифференциальные уравнения в частных производных?
4.Классифицируйте интегральное уравнение
x
(x) 2 (t)dt.
0
5.Поясните основные положения квазистатического подхода.
6.Почему внедиагональные элементы емкостной матрицы имеют отрицательные значения?
7.Опишите граничные условия на поверхности проводников
идиэлектриков.
8.Когда применим метод зеркальных уравнений?
9.Опишите процесс вычисления погонных параметров линии передачи.
–46 –
2 МЕТОДЫ РЕШЕНИЯ СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ (СЛАУ)
2.1 Общие сведения
2.1.1Постановка задачи
Ввычислительной линейной алгебре выделяют 4 основные задачи: решение СЛАУ; вычисление определителей; нахождение обратных матриц; определение собственных значений и собственных векторов. При этом решение СЛАУ называют первой основной задачей. Эффективность способа решения СЛАУ вида
Ax = b |
(2.1) |
во многом зависит от структуры матрицы A: размера, обусловленности, симметричности, заполненности (т.е. соотношения между числом ненулевых и нулевых элементов), специфики расположения ненулевых элементов в матрице и т. д. Будем полагать, что матрица А задана и является невырожденной. Известно, что в этом случае решение системы существует, единственно и устойчиво по входным данным, т. е. рассматриваемая задача корректна.
Пусть x* x1*, x2* , ..., x*N T приближенное решение СЛАУ
(T символ транспонирования). Будем стремиться к получению
решения, для которого погрешность e = x x* мала. Заметим, что качество полученного решения далеко не всегда характеризуется
тем, насколько мала погрешность x x* . Иногда вполне удовле-
творительным является критерий малости невязки r b Ax* . Так, вектор r показывает, насколько отличается правая часть системы от левой, если подставить в нее приближенное решение. За-
метим также, что r = Ax Ax* = A(x x*), поэтому погрешность и невязка связаны равенством
e x x* A 1r. |
(2.2) |
– 47 –

2.1.2 Нормы векторов
Решением СЛАУ является вектор x = (x1, x2, …, xN)T, который будем рассматривать как элемент векторного пространства CN.
Приближенное решение x* x1*, x2* , ..., x*N T |
и погрешность |
e x x* x1 x1*, x2 x2* , ..., xN x*N T также |
являются элемен- |
тами пространства CN. Для того чтобы анализировать методы решения СЛАУ, необходимо уметь количественно оценивать «вели-
чины» векторов x* |
и x – x*, а также векторов b и b – b*, где |
b* b1*, b2*, ..., bN* T |
– вектор приближенно заданных правых час- |
тей. Удобной для этой цели количественной характеристикой является широко используемое понятие нормы вектора.
Говорят, что в пространстве CN задана норма, если каждому вектору x из CN сопоставлено вещественное число ||x||, называемое нормой вектора x и обладающее следующими свойствами:
1)||x|| 0, причем ||x|| = 0 тогда и только тогда, когда x = 0;
2)|| x|| = | | ||x|| для любого вектора x и любого числа ;
3)||x + y|| ||x|| + ||y|| для любых векторов x и y.
Заметим, что такими же свойствами обладает обычная геометрическая длина вектора в трехмерном пространстве. Свойство 3 в этом случае следует из правила сложения векторов и из того известного факта, что сумма длин двух сторон треугольника всегда больше длины третьей стороны.
Существует множество различных способов введения норм. В вычислительных методах наиболее употребительными являются следующие три нормы:
N

 x
x
 1 | xi | – первая (манхэттенская, октоэдрическая) норма;
1 | xi | – первая (манхэттенская, октоэдрическая) норма;
i 1
|
|
|
|
N |
1/2 |
|
x |
|
2 |
|
| xi |2 |
|
вторая (евклидова норма, сферическая) |
|
|
|
i 1 |
|
|
|
|
|
|
|
|||
норма;
– 48 –
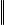
x |
|
|
|
|
max | xi | – бесконечная (равномерная, чебышевская, |
|
|
||||
|
|
|
|
1 i N |
|
|
|
|
|
кубическая) норма.
В определенном смысле эти нормы эквивалентны, так как каждая из них оценивается любой из двух других с точностью до множителя.
Пример 2.1
Найти нормы ||x||1, ||x||2, ||x|| для вектора x = (0.12, 0.15, 0.16)T.
Решение
По приведенным выше формулам имеем
||x||1 = 0.12 + 0.15 + 0.16 = 0.43, ||x||2 = (0.122 + 0.152 + 0.162)1/2 = 0.25,
||x|| = max{0.12, 0.15, 0.16} = 0.16.
2.1.3 Скалярное произведение векторов
Скалярным произведением векторов x = (x1, x2, …, xN)T и y = (y1, y2, …, yN)T называется величина xTy или
N
(x,y) x1 y1 ... xN yN xi yi .
i 1
Нетрудно заметить, что ||x||2 = (x, x)1/2. Когда векторы x и y имеют комплексные компоненты, скалярное произведение записывается в виде
N
(x,y) x1 y1 ... xN yN xi yi ,
i 1
где черта означает комплексное сопряжение.
2.1.4Абсолютная и относительная погрешности векторов
Далее будем всюду считать, что в пространстве N-мерных векторов CN введена и фиксирована некоторая норма ||x||. В этом
случае в качестве меры степени близости векторов x и x* естественно использовать величину ||x x*||, являющуюся аналогом
– 49 –
расстояния между точками x и x*. Введем абсолютную и относительную погрешности вектора x* с помощью формул
x* 
 x x*
x x* 
 ,
,
x* 
 x x*
x x* 

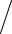

 x
x 
 .
.
Выбор той или иной нормы в практических задачах диктуется тем, какие требования предъявляются к точности решения. Выбор нормы ||x||1 фактически отвечает случаю, когда малой должна быть суммарная абсолютная погрешность в компонентах решения; выбор нормы ||x||2 соответствует критерию малости среднеквадратичной погрешности, а принятие в качестве нормы ||x|| означает, что малой должна быть максимальная из абсолютных погрешностей в компонентах решения.
2.1.5 Сходимость по норме
Пусть x(m) (m = 1, 2, …, ) последовательность векторов x(m) = (x1(m), x2(m), …, xN(m))T. Говорят, что последовательность векторов x(m) сходится к вектору x при m (x(m) x при m ),
если (x(m)) = ||x(m) x|| 0 при m .
Сам факт наличия или отсутствия сходимости x(m) к x при m в конечномерных пространствах не зависит от выбора нормы. Известно, что из сходимости последовательности по одной из норм следует сходимость этой последовательности по любой другой норме. Более того, x(m) x при m тогда и только то-
гда, когда для всех i = 1, 2, …, N имеем xi(m) xi при m , т. е. сходимость по норме в пространстве CN эквивалентна покомпо-
нентной (покоординатной) сходимости.
2.1.6 Нормы матриц
Величина
Ax
A max x (2.3)
x 0
называется нормой матицы A, подчиненной норме векторов, в CN. Понятиематрицы ввел Джеймс Джозеф Сильвестрв1850 г.
– 50 –
