
Электромагнитная совместимость
..pdf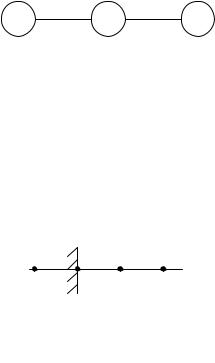
Необходимо отметить важность правосторонних и левосторонних разностей.
Рисунок 3.2 – Трехточечный шаблон для второй разностной производной (одномерный случай)
Так, на рисунке 3.3 схематично показана ситуация, когда неприменимы ни левосторонние, ни центральные разности, поскольку для их использования необходимо знать значение функции в точке x–1 (x0 – h).
Рисунок 3.3 – Случай применимости только правосторонних разностей
Оценим количественно ошибку конечно-разностных аппроксимаций. Это можно сделать, используя разложение функции в ряд Тейлора:
|
|
|
|
FD : f (x0 h2 ) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
f (x0 ) h2 f |
|
|
|
|
1 |
|
|
2 |
|
|
|
1 |
|
|
3 |
|
|
|
|
(3.4) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
(x0 ) |
2! |
h2 f |
(x0 ) |
3! |
|
h2 f |
(x0 ) ..., |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
BD: f (x0 h1) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
f (x |
) h f |
|
|
|
) |
1 |
|
|
h |
2 |
f |
|
(x ) |
1 |
|
|
h |
3 |
f |
|
(x |
) ... |
(3.5) |
||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
(x |
|
2! |
|
|
3! |
|
|
||||||||||||||||||
0 |
1 |
|
0 |
|
1 |
|
|
0 |
1 |
|
|
0 |
|
|
|||||||||||
Видно, что оценки (3.4) и (3.5) имеют погрешность порядка h1,2 (записывается как O(h1,2)), возникающую за счет отбрасывания высших членов ряда Тейлора. Вычтем (3.5) из (3.4):
|
f (x0 h2 ) f (x0 h1) |
|
||||
(h2 |
h1) f (x0 ) |
1 |
|
h22 h12 f (x0 ) O(h3 ). |
(3.6) |
|
2! |
||||||
|
|
|
|
|||
Поделив левую и правую части выражения (3.6) на h2 + h1, получим
– 101 –
f (x0 ) |
f (x0 h2 ) f (x0 h1) |
O(h2 h1), |
(3.7) |
|
|||
|
h2 h1 |
|
|
т.е. формулу, которая также имеет первый порядок погрешности. Однако при h1 = h2 = h в формуле (3.6) исчезает член, содержащий вторую производную, и тогда получим формулу
f (x0 ) |
f (x0 h) f (x0 h) |
O h |
2 |
, |
(3.8) |
2h |
|
||||
|
|
|
|
|
имеющую погрешность O h2 . Сложим (3.4) и (3.5):
f (x0 h) f (x0 h) 2 f (x0 ) h2 f (x0 ) O h4 . |
(3.9) |
Поделив это выражение на h2, получим производную (3.3), погрешность которой имеет порядок O h2 .
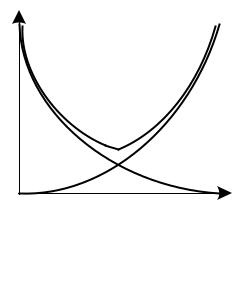
Таким образом, погрешность конечно-разностных формул определяется значением шага h. Чем меньше шаг, тем формула точнее. Однако при неограниченном уменьшении шага погрешность вычисления производных начинает увеличиваться, так как при этом разность между значениями функции в соседних узлах сетки уменьшается, что приводит к возрастанию влияния ошибок округления. Типовая зависимость погрешности конечно-разностной формулы от шага сетки показана на рисунке 3.4.
Рисунок 3.4 – Зависимость погрешности конечно-разностной аппроксимации от шага сетки: d – погрешность, вызванная отбрасыванием высших членов ряда Тейлора; – погрешность, вызванная конечной точностью представления чисел;
– суммарная погрешность
– 102 –

3.2 Способы повышения точности вычислений
3.2.1 Разложение в ряд Тейлора
Рассмотрим способы повышения точности. Сначала используем трехточечный шаблон и правосторонние разности. Для этого потребуются три точки: x0, x0+h, x+2h. Далее воспользуемся разложением в ряд Тейлора функции в этих точках:
f (x0 h) f (x0 ) hf (x0 ) 12 h2 f (x0 ) O h3 ; f (x0 2h) f (x0 ) 2hf (x0 ) 2h2 f (x0 ) O h3 .
Вычитая второе уравнение из первого, умноженного на 4, получим выражение для производной FD:
|
4 f (x0 |
h) f (x0 |
2h) 3 f (x0 ) |
|
(3.10) |
fFD (x0 ) |
|
|
|
. |
|
|
2h |
|
|||
|
|
|
|
|
При использовании трехточечного шаблона и левосторонних разностей запишем
f (x0 h) f (x0 ) hf (x0 ) 12 h2 f (x0 ) O h3 , f (x0 2h) f (x0 ) 2hf (x0 ) 2h2 f (x0 ) O h3 .
Также вычтем второе уравнение из первого, умноженного на 4:
4f (x0 h) f (x0 2h) 3 f (x0 ) 2hf (x0 ) O h3 .
Врезультате получим выражение для производной BD:
fBD (x0 ) 3 f (x0 ) 4 f (x02hh) f (x0 2h) .
Ее погрешность имеет порядок O h2 .
Применим пятиточечный шаблон (центральные разности). Для этого потребуется пять точек: x0 – 2h, x0 – h, x, x0 + h, x + 2h. Далее воспользуемся разложением в ряд Тейлора функции в этих точках:
– 103 –

f (x0 h) |
f (x0 ) hf (x0 ) |
1 |
|
h2 f (x0 ) |
|
1 |
|
h3 f (x0 ) O h4 ; |
|||||||
2! |
3! |
||||||||||||||
|
|
|
|
|
|
|
|
||||||||
f (x0 h) |
f (x0 ) hf (x0 ) |
1 |
|
h2 f (x0 ) |
|
1 |
|
h3 f (x0 ) O h4 ; |
|||||||
2! |
3! |
||||||||||||||
|
|
|
|
|
|
|
|
||||||||
f (x0 2h) |
f (x0 ) 2hf (x0 ) |
4 |
|
h2 f (x0 ) |
8 |
|
h3 f (x0 ) O h4 ; |
||||||||
2! |
3! |
||||||||||||||
|
|
|
|
|
|
|
|||||||||
f (x0 2h) |
f (x0 ) 2hf (x0 ) |
4 |
|
h2 f (x0 ) |
|
8 |
|
h3 f (x0 ) O h4 . |
|||||||
2! |
3! |
||||||||||||||
|
|
|
|
|
|
|
|||||||||
Вычитая второе уравнение из первого и четвертое из третьего, получим
Sh: |
f (x0 h) f (x0 |
h) 2hf (x0 ) |
1 h3 f (x0 ) O h4 , |
|
||||
|
|
|
|
3 |
|
|
|
|
S2h: |
f (x0 2h) f (x0 |
2h) 4hf (x0 ) 8 h3 f (x0 ) O h4 |
. |
|||||
|
|
|
|
3 |
|
|
|
|
Для исключения f'''(x0) вычислим 8Sh–S2h: |
|
|
|
|||||
|
|
8 f (x0 h) 8 f (x0 h) f (x0 |
2h) |
|
|
|
||
|
|
f (x0 2h) 12hf (x0 ) O |
h4 . |
|
|
|
||
В результате получим первую производную |
|
|
|
|||||
|
|
8 f (x0 h) 8 f (x0 h) f (x0 |
2h) f (x0 |
2h) |
|
(3.11) |
||
fCD |
(x0 ) |
|
|
|
|
|
, |
|
|
12h |
|
|
|
||||
|
|
|
|
|
|
|
|
|
погрешность которой имеет порядок O h4 .
Для нахождения второй производной запишем:
f(x0 h) f (x0 ) hf (x0 )
h5
120
f(x0 h) f (x0 ) hf (x0 )
h5
120
|
h2 |
|
h3 |
|
h4 |
f |
(4) |
(x0 ) |
|
|
|
|
|
||||||
2 |
f (x0 ) |
8 |
f (x0 ) |
24 |
|
||||
|
|
|
|
|
|
|
|||
f (5) (x0 ) O h6 ; |
|
|
|
|
|||||
|
h2 |
|
h3 |
|
|
h4 |
f |
(4) |
(x0 ) |
|
|
|
|
|
|||||
2 |
f (x0 ) |
8 |
f (x0 ) |
24 |
|
||||
|
|
|
|
|
|
|
|||
f (5) (x0 ) O h6 ;
– 104 –

|
|
|
|
|
|
2 |
f |
|
4h3 |
f |
|
|||
|
|
|
|
|
|
|
||||||||
f (x0 2h) f (x0 ) 2hf (x0 ) 2h |
|
|
(x0 ) |
3 |
|
(x0 ) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2h4 |
f (4) (x0 ) |
32h5 |
f (5) |
(x0 ) O h6 ; |
|
|
|||||||
3 |
120 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
4h3 |
|
|
|||
|
|
|
|
|
|
2 |
f |
|
|
f |
|
|||
|
|
|
|
|
|
|
|
|||||||
f (x0 2h) f (x0 ) 2hf (x0 ) 2h |
|
|
(x0 ) |
3 |
|
(x0 ) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2h4 |
f (4) (x0 ) |
32h5 |
f (5) |
(x0 ) O h6 . |
|
|
||||||
|
3 |
120 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Сложив первое уравнение со вторым и третье с четвертым, получим
Sh: f (x0 h) f (x0 h) 2 f (x0 ) h2 f (x0 ) h2 f (4) (x0 ) O h6 , 12
S2h: f (x0 2h) f (x0 2h) f (x0 ) 4h2 f (x0 ) 34 h2 f (4) (x0 ) O h6 .
Для исключения f(4)(x0) вычислим Sh–S2h/16:
f (x0 h) f (x0 h) f (x0 2h) f (x0 2h)
158 f (x0 ) 34 h2 f (x0 ) O h6 .
Врезультате получим производную
fCD (x0 )
f (x0 2h) 16 f (x0 h) 30 f (2x0 ) 16 f (x0 h) f (x0 2h) , 12h
(3.12)
погрешность которой имеет порядок O h4 .
3.2.2 Интерполяционные полиномы
Рассмотрим другой способ получения конечно-разностных аппроксимаций, заключающийся в использовании интерполяционных полиномов вида
PN 1(x) Nj 01a j x j .
– 105 –
Тогда в окрестности x0 можно предположить, что f'(x0) P'(x0) и f''(x0) P''(x0). Здесь N – нечетное количество эквидистантных точек в окрестности x0, таких, что fk = f(xk), xk = x0 + kh, k = –(N–1)/2, …, (N+1)/2. Используя введенные обозначения, получим систему уравнений
{PN–1(xk) = fk}, k = –(N–1)/2, …, (N+1)/2.
Рассмотрим процесс нахождения f (x0 ) и f (x0 ) при N = 3, для простоты полагая x0 = 0. Запишем интерполяционный полином
PN 1(x) a0 a1x a2 x2 .
Тогда f'(0) P'(0) = a1, f''(0) P''(0) = 2a2. Таким образом, для нахождения значений производных необходимо найти коэффициенты a1 и a2. Для этого запишем систему уравнений
P2 ( h)P2 (0)P2 (h)
f |
1 |
a |
a h a h2 |
f |
1 |
||
|
|
0 |
1 |
2 |
|
||
f0 |
|
|
a0 f0 |
|
. |
||
f1 |
a |
a h |
a h2 |
f |
|||
|
|
|
0 |
1 |
2 |
|
1 |
Вычитая первое уравнение из третьего, получим
f (0) P (0) a1 f 1 f1 , 2h
а сложив их и используя второе уравнение, получим 2f0 + 2a2h2 = = f–1 + f1. Тогда
|
P |
|
2a2 |
|
f 1 2 f0 |
f1 |
. |
|
|
||||||
f (0) |
(0) |
h2 |
|
||||
|
|
|
|
|
|
|
Видно, что данные выражения аналогичны формулам (3.2) и (3.3).
Повышение точности аппроксимации производных возможно за счет увеличения степени интерполяционного полинома и использования большего числа точек, чем это необходимо для вычисления производной данного порядка. Рассмотрим процесс нахождения f (x0 ) P (x0 ) и f (x0 ) P (x0 ) при N = 5 (пятиточечный шаблон). В данном случае получим следующую систему уравнений:
– 106 –

P4 ( 2h) |
|
|
P ( h) |
|
4 |
|
P4 (0) |
|
|
|
P (h) |
|
4 |
|
P (2h) |
|
4 |
f 2 |
a |
2a h 4a h2 |
a h3 |
16a h4 |
|
f |
2 |
|||||||||
|
0 |
|
1 |
2 |
|
3 |
|
4 |
|
|
|
|
|
|||
f |
1 |
|
|
a |
a h a h2 |
a h3 |
a h4 |
|
f |
1 |
|
|||||
|
|
|
0 |
1 |
2 |
|
3 |
|
4 |
|
|
|
|
|||
f0 |
|
|
|
|
a0 f0 |
|
|
|
|
|
|
|
. |
|||
f1 |
|
|
a |
a h a h2 |
a h3 |
a h4 |
|
f |
|
|
||||||
f2 |
|
|
0 |
1 |
2 |
|
3 |
|
4 |
|
|
|
1 |
|
|
|
|
|
|
2a1h 4a2h |
2 |
a3h |
3 |
16a4h |
4 |
f2 |
|||||||
|
|
a0 |
|
|
|
|||||||||||
Вычитая первое уравнение из пятого и второе из четвертого, получим систему
|
|
|
|
|
3 |
f 2 |
f2 |
|
|
|||||
|
4a1h 16a3h |
|
, |
|
||||||||||
|
|
2a h 2a h3 |
f f |
|
|
|
||||||||
|
|
1 |
|
|
|
|||||||||
|
|
1 |
|
3 |
|
|
1 |
|
|
|
|
|
||
а сложив их, – |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
32a4h |
4 |
f 2 |
f2 |
|
||||||
2a0 8a2h |
|
|
. |
|||||||||||
|
2a |
2a h2 2a h4 |
|
f |
|
|
f |
|||||||
|
1 |
|
||||||||||||
|
0 |
2 |
|
|
|
4 |
|
|
|
|
1 |
|
||
Решая первую из этих систем относительно a1, найдем
f (0) P (0) a1 f 2 8 f1 8 f 1 f2 . 12h
Данное выражение эквивалентно (3.11), полученному с помощью разложения в ряд Тейлора. Решая вторую систему относительно a2 (при a0 = f0), найдем
f (0) P (0) 2a2 f 2 16 f 1 302f0 16 f1 f2 . 12h
Погрешность имеет порядок O h4 . Данное выражение экви-
валентно (3.12), полученному с помощью разложения в ряд Тейлора.
Запишем итоговые формулы для производных, полученные с помощью семиточечного шаблона (N = 7):
f (0) f 3 9 f 2 45 f 1 45 f1 9 f2 f3 , 60h
f (0) 2 f 3 27 f 2 270 f 1 490 f0 270 f1 27 f2 2 f3 . 12h2
– 107 –
3.2.3 Многочлены Лагранжа
Рассмотрим способ получения конечно-разностных аппроксимаций за счет использования многочленов Лагранжа. Напомним, что интерполяционный многочлен Лагранжа – это многочлен минимальной степени, принимающий данные значения в данном
наборе точек. Для n + 1 пар чисел (x0, f(x0)), (x1, f(x1)),…, (xn, f(xn)),
где все x j различны, существует единственный многочлен L(x)
степени не более n, для которого P(xj) = f(xj).
В общем виде базисные полиномы P(x) определяются по формуле
|
P (x) f (x ) |
(x x1)(x x2 )...(x xk ) |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
n |
|
|
0 |
|
|
(x |
|
x )(x |
x )...(x |
x ) |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
0 |
|
1 |
|
|
0 |
|
2 |
|
|
0 |
|
k |
|
|
|
|
|
|
||
|
f (x ) |
(x x0 )(x x2 )...(x xk ) |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
1 |
|
(x |
x )(x |
x |
|
)...(x x ) |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
1 |
|
|
|
0 |
1 |
|
|
2 |
|
1 |
|
k |
|
|
|
|
|
|
|
|
|||
|
... f (xk ) |
|
|
(x x0 )(x x1)...(x x j ) |
|
|
. |
|
|
|
|||||||||||||||||
|
(x |
|
x )(x |
|
x )...(x |
x |
j |
) |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
k |
|
|
0 |
|
k |
|
2 |
|
|
k |
|
|
|
|
|
|
|
|
||
Для нахождения |
f (x0 ) |
|
достаточно трех точек: x0, x1 = x0 + h, |
||||||||||||||||||||||||
x2 = x0 + 2h. Тогда итоговый полином имеет вид |
|
|
|
|
|
|
|
|
|||||||||||||||||||
P (x) f (x ) |
(x x1)(x x2 ) |
|
|
f (x |
) |
(x x0 )(x x2 ) |
|
|
|||||||||||||||||||
|
|
) |
|
|
|
||||||||||||||||||||||
3 |
0 |
(x |
x )(x |
x |
|
|
|
1 |
|
(x x )(x |
x ) |
||||||||||||||||
|
|
0 |
|
1 |
|
0 |
2 |
|
|
|
|
|
|
|
1 |
|
0 |
|
|
|
1 |
2 |
|
|
|||
|
|
f (x ) |
|
(x x0 )(x x1) |
. |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
2 |
(x |
x |
)(x x ) |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
2 |
|
0 |
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
||
Продифференцировав его и сделав замену x на x0, x1 на x0+h и |
|||||||||||||||||||||||||||
x2 на x0 + 2h, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
3 f (x0 ) 4 f (x0 |
h) f (x0 2h) |
|
|
|||||||||||||||||
fFD |
(x0 ) P3 (x0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||
|
|
|
|
|
|
|
|
|
2h |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Данное выражение эквивалентно (3.10), а его погрешность |
|||||||||||||||||||||||||||
будет O h2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Далее найдем f''(x0) с погрешностью O h2 , используя право-
сторонние разности. Для этого потребуются четыре точки: x0, x1 = x0 + h, x2 = x0 + 2h и x3 = x0 + 3h. Тогда
– 108 –
P |
(x) f |
(x ) |
|
(x x1)(x x2 )(x x3 ) |
|
|
|||||||||||||||||||
|
|
|
) |
||||||||||||||||||||||
4 |
|
|
|
|
0 |
(x |
x )(x |
x )(x |
x |
|
|||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
1 |
|
0 |
|
|
2 |
|
0 |
|
|
|
|
3 |
|
|
|
|
f (x |
) |
|
|
(x x0 )(x x2 )(x x3 ) |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
) |
|
|
|
||||||||||||||||||
|
1 |
|
(x |
x |
)(x |
x |
|
)(x |
x |
|
|
|
|
|
|||||||||||
|
|
|
|
|
1 |
|
|
0 |
|
1 |
|
2 |
|
1 |
|
|
3 |
|
|
|
|
|
|
|
|
|
f (x |
) |
|
|
(x x0 )(x x1)(x x3 ) |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
) |
|
|
||||||||||||||||||
|
2 |
|
(x |
|
x |
)(x |
|
x )(x |
|
x |
|
|
|
|
|
||||||||||
|
|
|
|
|
2 |
|
|
0 |
|
2 |
|
|
1 |
2 |
|
|
3 |
|
|
|
|
|
|
||
|
f (x3 ) |
(x x0 )(x x1)(x x2 ) |
|
|
|
. |
|
|
|||||||||||||||||
|
(x |
|
x |
|
)(x |
|
x |
)(x |
|
x |
|
|
) |
|
|
||||||||||
|
|
|
|
|
3 |
|
0 |
3 |
|
1 |
3 |
|
2 |
|
|
|
|
|
|||||||
Продифференцировав дважды многочлен P4(x) и заменив x на x0, x1 на x0 + h, x2 на x0 + 2h и x3 на x0 + 3h, получим производную
|
|
2 f (x0 ) 5 f (x0 h) 4 f (x0 2h) f (x0 |
3h) |
, |
|
|
|||
fFD (x0 ) P4 (x0 ) |
h2 |
|
||
погрешность которой имеет порядок O h2 .
В таблице 3.1 приведены часто используемые конечно-раз- ностные аппроксимации с указанием их погрешности.
|
Таблица 3.1 |
|
– |
Конечно-разностные аппроксимации и их |
|||||||||||
погрешность |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Конечно-разностная аппроксимация |
Погрешность |
||||||||||||
|
|
|
|
|
|
|
|
f (x0 h) f (x0 ) |
|
|
|||||
|
|
|
fFD (x0 ) |
|
|
|
|
|
|
O(h) |
|||||
|
|
|
h |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
f (x0) f (x0 h) |
|
|
|||||
|
|
|
fBD(x0) |
|
|
|
|
|
|
O(h) |
|||||
|
|
|
h |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
f |
(x0 h) f (x0 h) |
2 |
|
||||||
|
|
fCD(x0) |
|
|
|
|
|
|
|
O(h |
) |
||||
|
|
|
2h |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
4 f (x0 h) f (x0 2h) 3 f (x0) |
2 |
) |
|||||||||
|
fFD(x0) |
|
|
|
|
2h |
O(h |
||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
3 f (x0) 4 f (x0 h) f (x0 2h) |
2 |
|
|||||||||
|
fBD(x0) |
|
|
|
|
|
|
|
|
|
|
|
O(h |
) |
|
|
|
|
|
|
2h |
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
8 f (x0 h) 8 f (x0 h) f (x0 2h) f (x0 2h) |
4 |
) |
|||||||||||
fCD(x0) |
|
|
|
|
|
|
12h |
O(h |
|||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
f |
(x0 2h) 2 f (x0 h) f (x0 ) |
|
2 |
) |
||||||
|
|
|
|
|
|
||||||||||
|
fFD(x0) |
|
|
|
|
h2 |
O(h |
||||||||
|
|
|
|
|
|
|
|
|
|
||||||
– 109 –
Окончание таблицы 3.1
|
Конечно-разностная аппроксимация |
Погрешность |
||||||||||
|
|
|
|
f (x0 ) 2 f (x0 h) f (x0 2h) |
|
|
2 |
) |
||||
|
|
|
|
|
||||||||
|
fBD (x0 ) |
|
|
|
h2 |
|
|
|
|
O(h |
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
f |
(x0 h) 2 f (x0) f (x0 h) |
|
|
2 |
) |
|||
|
|
|
|
|
||||||||
|
fCD(x0 ) |
|
h2 |
|
|
|
|
|
O(h |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fCD (x0 ) |
|
|
|
|
|
O(h4) |
|
|
f (x 2h) 16 f |
(x h) 30 f (x ) |
16 f (x h) |
f (x 2h) |
||||||||
0 |
|
|
0 |
0 |
0 |
0 |
|
|
|
|||
|
|
|
|
|
12h2 |
|
|
|
|
|
|
|
3.3Решение эллиптических уравнений
3.3.1Двухмерное уравнение Лапласа: однородный
диэлектрик
Первая проблема, с которой приходится сталкиваться при реализации конечно-разностного метода, – это вывод конечноразностных уравнений в исследуемой пространственной области из соответствующего дифференциального уравнения в частных производных. Когда для анализа линии передачи используется уравнение Лапласа, распределение потенциала ищется в ограниченной области, которая разбивается координатными линиями на некоторое число элементарных ячеек. Каждая точка пересечения двух линий, являющихся сторонами ячейки, образует узел. Значения потенциала в узловых точках и являются искомыми величинами.
В двухмерном случае простейшая равномерная сетка соответствует декартовой системе координат и состоит из прямоугольных ячеек. Из каждого узла сетки, двигаясь вдоль сторон ячеек, можно попасть в четыре соседних узла (рисунок 3.5, а). Такая сетка называется пятиточечной. Если рассматривается трехмерная задача, то при движении по сетке из каждого узла можно попасть в шесть соседних. В этом случае сетка семиточечная.
Применим конечно-разностный подход, чтобы найти решение функции Ф, зависящей от двух пространственных переменных x и y (уравнение Лапласа):
– 110 –
