Технология кремниевой наноэлектроники

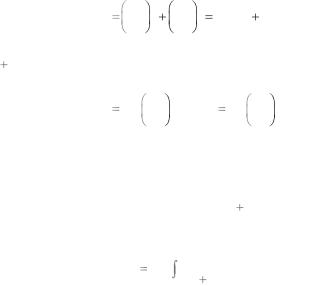
Теория, которая позволяет рассчитать пробеги ионов в твердых телах, была разработана Линдхардом, Шарфом и Шиоттом (ЛШШ).

Втеорию заложены следующие предположения:

1)твердые тела, с которым взаимодействуют ионы, являются однородными, изотропными с неупорядоченным расположением атомов (приближение аморфной мишени);

2)упругие и неупругие взаимодействия происходят независимо друг от друга (принцип аддитивности);

3)в атомных столкновениях ионы теряют энергию, много меньшую начальной энергии иона, что позволяет применить статистический подход к расчету пробега ионов.

Согласно принципу аддитивности выражение для средней величины потерь энергии одного иона в твердом теле имеет вид

способностей заключается в том, что они определяют потери энергии иона в ядерных (атомных) и электронных столкновениях соответственно в твердом теле с единичной плотностью атомов при прохожде-

глубину проникает внедренный ион. Справедливо и обратное утверждение. Величины Sя и Se зависят от энергии иона, атомного номе-

каждой комбинации ион–мишень.

101

ЛШШ упростили эту задачу, введя безразмерные (нормированные) значения энергии и пробега :

Коэффициенты F и L являются нормированными множителями энергии и пробега соответственно. С учетом этих коэффициентов ядерная и электронная тормозные способности, имеющие уже универсальный характер, примут вид

Рис. 6.4. Зависимость тормозных способностей от 1/2 : 1 – ядерная тормоз-

ная способность; 2 – электронная тормозная способность; 3 – Sян

102

Преимущество введения безразмерных параметров и состоит в том, что зависимость Sян или (d / d )я от 1/2 является универ-

сальной, т.е. применима для любых пар ион–атом. Ядерное торможение при малых энергиях иона возрастает, достигая максимального значения при 1 0,35, а затем медленно спадает с ростом энергии,

т.к. быстрые частицы имеют меньшее время взаимодействия с центром рассеяния, т.е. поперечное сечение для них уменьшается.

Ядерная тормозная способность Sяно 0,327 и является своеоб-

разным средним значением для Sян ( 1/2 ) (см. рис. 6.4). Простая аналитическая аппроксимация найдена Юдиным:

где A 0,45; B 0,30.

Переход от нормированной величины ядерной тормозной способности к размерному ее значению осуществляется с помощью соотношения

Электронная тормозная способность. По теории ЛШШ па-

дающий ион теряет свою энергию как при близких столкновениях с электронами, так и на возбуждение электронного газа в объеме, удаленном от траектории иона. Пока скорость иона меньше скорости

электронов, соответствующих энергии Ферми, величина Seн остается

пропорциональной скорости иона или корню квадратному из его энергии

Таким образом, электронное торможение графически можно представить не одной кривой, а семейством прямых, выходящих из

начала координат. Наклон прямых к оси 1/2 определяется множителем k и для ионов, представляющих практический интерес, лежит в диапазоне k 0,10 0,25 при Z1 Z2 , но если ионы легкие и Z1 Z2 ,

103

где arctg подставляется в радианах.

Средний полный пробег рассчитывается в соответствии с фор-

гия, затраченная ионом на упругие столкновения, которую В.В. Юдин аппроксимирует выражением вида

A

я k ln 1 A k B .

104

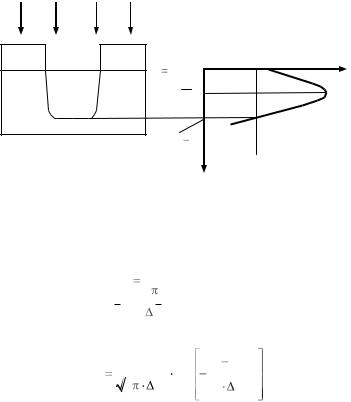
6.3.Распределение внедренной примеси по глубине

Врезультате торможения ионов в материале мишени они останавливаются на определенных глубинах, изменяя первоначальные свойства вещества. В полупроводниковой технологии ионная имплантация обладает рядом преимуществ по сравнению с термическим диффузионным методом введения примесей. Внедряя ионы III и V групп в монокристалл Si , можно получить p-n - и n-p -переходы в

любом месте на любой площади. Сначала на кремниевой пластине формируется защитная маска с помощью фотолитографии, затем осуществляется локальная имплантация примесей в полупроводник (рис. 6.5). В качестве маски чаще всего используются слои SiO2 с

толщиной, большей, чем пробег ионов в SiO2 .

Р

Рис. 6.5. Пример ионной имплантации фосфора в кремний p-типа

Для аморфных мишеней распределение пробегов приблизительно гауссово и поэтому может быть охарактеризовано среднеквадра-

Зная величины Rρ и Rρ , распределение внедренной примеси по глубине N (x) вычисляется с помощью выражения

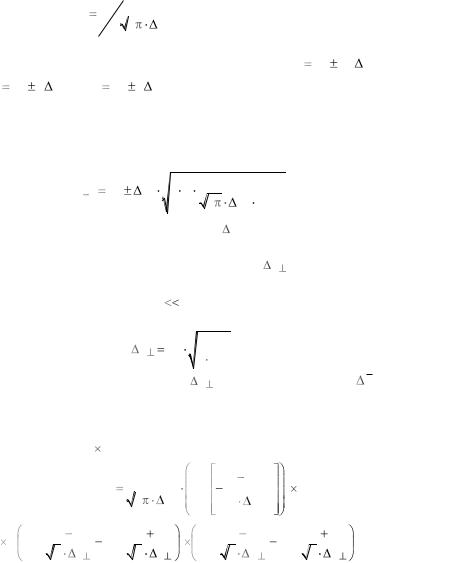
где x – расстояние от поверхности вглубь полупроводника в направлении падения ионов. Максимальная концентрация внедренной при-

Концентрация спадает и уменьшается в 2, 10 и 100 раз по отношению

в той области полупроводника, куда ведется имплантация. Решая это уравнение, получим

гая величина, имеющая важное значение для практических применений ионного легирования, – боковое рассеяние R , т.е. рассеяние, которое претерпевают падающие ионы от направления x . Для расчета этой величины при M 2 / M1 1 можно воспользоваться простым выражением

Значения бокового рассеяния R несколько выше, чем Rρ .

Однако они значительно меньше боковой диффузии, которая имеет порядок глубины диффузии, перпендикулярной к поверхности. В том случае, когда имплантацию проводят через прямоугольное окно в маске размером 2a 2b, профиль описывается формулой

(6.15)

где символом erfc обозначена функция дополнения интеграла ошибок до единицы. Концентрация легирующей примеси на краю маски па-

106

где N (x) – распределение по глубине подложки на большом расстоя-

нии от края маски.

Распределение примеси при ионном легировании в двухслой-

ные мишени. В технологии ионного легирования часто используют имплантацию примеси в полупроводники с предварительно нанесенным на его поверхность маскирующим слоем, например: двуокиси кремния SiO2 , окиси алюминия Al2O3 , нитрида кремния Si3N4 , а

также тонких напыленных металлических пленок.

При построения профиля в двухслойных структурах исходят из гауссовского распределения пробегов ионов в обеих составляющих

Распределения концентрации примеси в маскирующем слое N1(x) и в полупроводнике N2 (x) определяются следующими выражениями:

Распределение примеси с учетом эффекта распыления полупроводника в процессе легирования. При легировании материалов большими дозами наблюдается эффект распыления поверхности мишени ионами, что ведет к изменению профиля распределения имплантированной примеси. Основным параметром, характеризующим процесс распыления, является коэффициент распыления K, т.е. число атомов, выбиваемых одним падающим ионом. Толщина распыленного слоя материала мишени равна

107

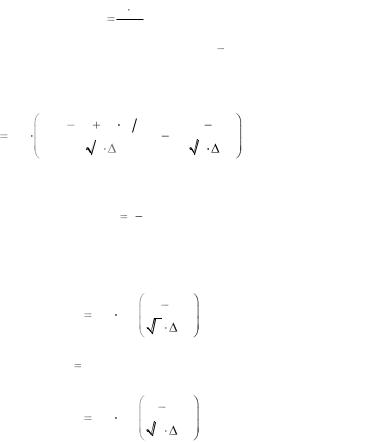
hQ K , м, N0

где K – коэффициент распыления, ат./ион; Q доза облучения, ион/м2; N0 – плотность атомов в мишени, ат/м3.

Профиль легирования с учетом распыления определяется теперь

где erf – функция ошибок.

Между нею и дополнительной функцией ошибок erfc существует зависимость

erfc(x) 1 erf (x).

Насыщение профиля легирования происходит при равенстве чисел внедренных ионов и распыленных с поверхности мишени атомов. В этом случае распределение внедряемых ионов по глубине описывается выражением

Эта максимальная концентрация не зависит от дозы имплантации Q, а определяется в основном отношением атомной плотности материала N0 к коэффициенту распыления K.

Эффект каналирования

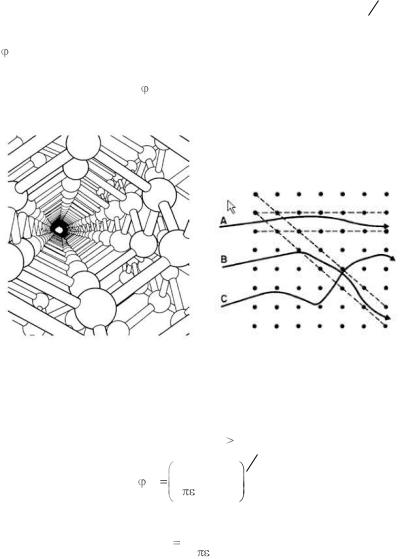
Рассмотренная теория ЛШШ описывает пробеги ионов в аморфных мишенях. В то же время полупроводники являются монокристаллическими веществами, т.е. имеют упорядоченное расположение атомов, характеризуемое кристаллографическими направлениями и плоскостями (рис. 6.6). Ионы, двигаясь вдоль кристаллографических направлений, например вдоль <100> в решетке алмаза, проникают глубже в кристалл, чем это следует из теории ЛШШ (эффект каналирования). В этих каналах ионы практически не испытывают атомных

108

столкновений, и их торможение обусловлено главным образом элек-

тронными столкновениями, т.е. пробег иона пропорционален E012 .

Линдхард рассмотрел задачу определения критического угла кр , под которым ион может войти в канал и при дальнейшем дви-

жении не покинет его. Если угол падения ионного пучка относительно канала будет больше кр , то ионы не будут захватываться в канал,

и монокристаллическую мишень можно рассматривать как аморфную.

а б

Рис. 6.6. Схема эффекта каналирования: а – кристаллическая структура типа алмаза в направлении 110; б – различные варианты каналирования

Критический угол Линдхард определяет в зависимости от энер-

где dhkl – расстояние между атомами в ряде направления с индексами h, k, l; a – радиус экранирования атома Томаса–Ферми;

б) для энергий ионов, меньших Eкр , имеем

109

где C 3.

Как видно из формул, критический угол по мере уменьшения энергии ионов E0 и увеличения атомных номеров иона и атома ми-

шени возрастает и, следовательно, каналирование облегчается. Критический угол каналирования зависит также от кристаллографическо-

Падающие ионы можно разделить на три группы:

1) группа А – это те частицы, которые входят в канал под углами кр , поэтому они имеют большую вероятность остаться в нем в

течение всего процесса замедления;

2)группа В – это те частицы, которые с самого начала движутся

вканалах с большой амплитудой осцилляций. Для таких частиц велика вероятность рассеяния с отклонением от первоначального направления, т.е. велика вероятность деканалирования, поэтому они не проникают так глубоко, как частицы группы С;

3)группа С – это те частицы, которые входят в канал под боль-

тру канала, т.е. они не чувствуют кристалличности, и распределение их пробегов будет такое же, как в аморфных материалах.

Для большинства кристаллов большую роль играет эффект деканалирования, поэтому большая асть ионов останавливается в области В.

Степень деканалирования зависит от многих факторов, таких, как температура мишени, поверхностные загрязнения, небольшая разориентировка или расходимость ионного пучка. Даже если вначале имеется совершенный монокристалл, то с увеличением количества

110