Радиоавтоматика

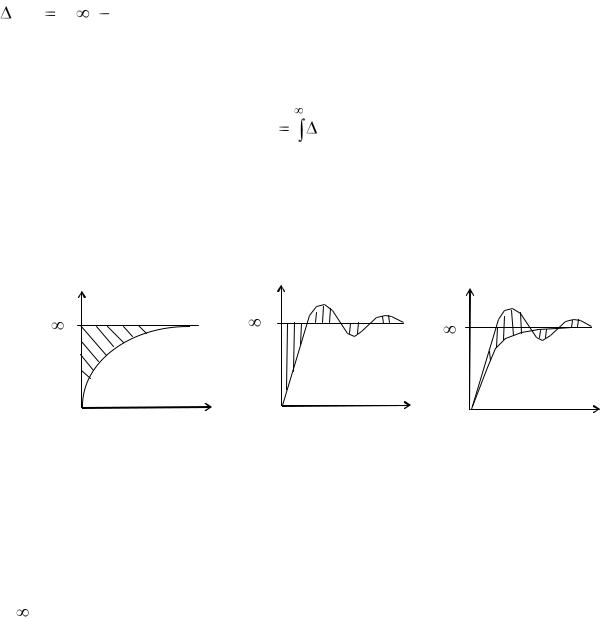
211

13.4.4. Интегральные критерии качества

переходных процессов

Интегральными называются критериями качества переходных процессов такие, которые одним числом оценивают величины отклонений и время затухания переходного процесса. Обозначим отклонение переходной

(рис. 13.22,а) интегральной оценкой служит заштрихованная площадь над кривой в виде

Рис. 13.22. Интегральные критерии качества

переходного процесса

Однако для колебательного процесса такая оценка качества переходного процесса не годится, так как площади, расположенные выше и ниже прямой h( ) , будут иметь разные знаки. Поэтому по минимуму величины I1

наилучшим оказался бы процесс с незатухающими колебаниями.

212

В связи с этим в общем случае принимают квадратичную

интегральную оценку качества (рис. 13.22,б) в виде

Влитературе имеются формулы, выражающие величину I 2

непосредственно через коэффициенты дифференциального уравнения замкнутой системы.

Очевидно, что стремление оценки I 2 к нулю приближает кривую процесса к скачку, ибо при этом уменьшается квадратичная площадь,

ограниченная кривой. Однако это вызывает значительное увеличение скорости в начальной части процесса. Для быстро затухающего, но достаточно плавного процесса вводят улучшенную квадратичную интегральную оценку качества переходного процесса (рис. 13.22,в) в виде следующего выражения:

где T — желаемая постоянная времени экспоненты, к которой стремится кривая переходного процесса.

Интегральные критерии качества применяются для определения оптимальных значений варьируемых параметров по минимуму значения соответствующей интегральной оценки. Численной оценки показателей качества они не дают.

213

14. КОРРЕКЦИЯ ДИНАМИЧЕСКИХ СВОЙСТВ ЛИНЕЙНЫХ САР

14.1. Схемы включения корректирующих звеньев

Коррекция динамических свойств САР осуществляется для обеспечения требований по точности, устойчивости и качеству переходного процесса.

Коррекцию динамических свойств САР можно сделать двумя способами:

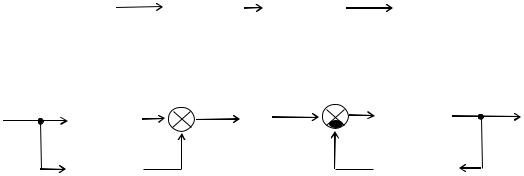
изменением параметров звеньев данной системы; изменением структуры системы с помощью введения корректирующих звеньев. Корректирующие звенья могут включаться последовательно или параллельно с основными звеньями САР (рис. 14.1) [1–4].

а— последовательная; б — параллельная;

в— с обратной связью.

Результирующие желаемые передаточные функции W Ж ( p)

соответственно для схем последовательного, параллельного включения

корректирующих звеньев и включения с обратной связью находятся из

соотношений:

14.2. Последовательные корректирующие звенья

Наибольшее применение получили следующие последовательные

корректирующие звенья:

пропорционально-дифференцирующее;

пропорционально-интегрирующее;

пропорционально-интегродифференцирующее.

14.2.1. Пропорционально-дифференцирующее звено

звено.

Последовательное включение пропорционально-дифференцирующего звена в САР приводит к тому, что передаточная функция разомкнутой системы

Из выражения (14.15) следует, что в передаточную функцию вводится нуль, причем положительное воздействие по производной, когда нуль

216

находится в левой полуплоскости (см. рис. 13.17,д), приводит к повышению устойчивости системы и качества переходного процесса.

АФХ, ЛАЧХ и ЛФЧХ идеального пропорционально-дифференцирующего звена для положительного воздействия по производной с учетом (14.14)

соответственно запишутся:

звено имеет следующую передаточную функцию

АФХ, ЛАЧХ и ЛФЧХ инерционного пропорционально-

дифференцирующего звена для положительного воздействия по производной с учетом (14.19) соответственно запишутся:

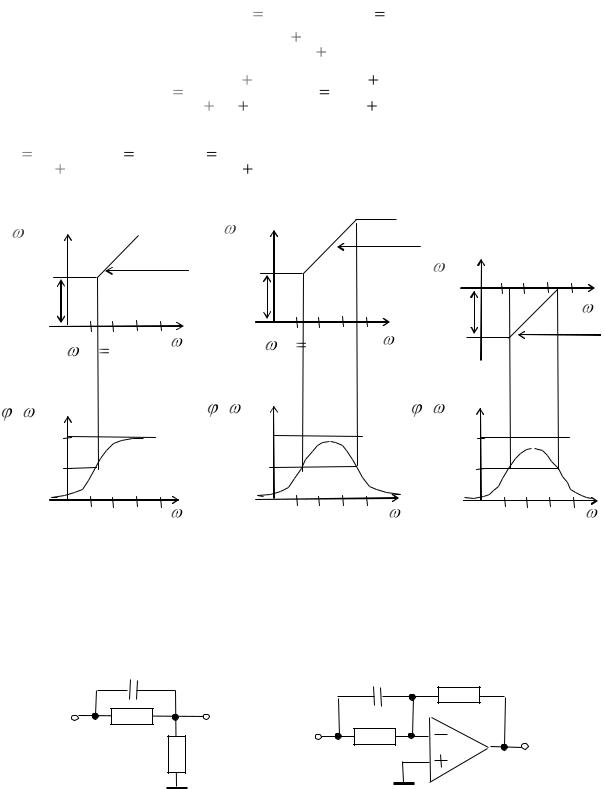
На рис. 14.2,а,б приведены АЛАЧХ и ЛФЧХ для идеального и инерционного пропорционально-дифференцирующих звеньев.

Пропорционально-дифференцирующие звенья реализуются на основе

RC - звена и ОУ (рис. 14.3).

Найдем передаточную функцию пропорционально-дифференцирующего звена, реализованного на основе RC -звена

Рис. 14.2. Логарифмические частотные характеристики пропорционально-дифференцирующих звеньев: а — идеального; б — инерционного; в — на основе RC -звена.

Рис. 14.3. Принципиальные схемы пропорционально-дифференцирующих звеньев: а — на основе RC-звена; б — на основе ОУ

218

Ввыражении (14.23) слагаемое в знаменателе pT2 определяет

неидеальность реализации пропорционально-дифференцирующего звена,

реализованного на основе RC -звена

АФХ, ЛАЧХ и ЛФЧХ пропорционально-дифференцирующего звена,

реализованного на основе RC -звена, с учетом (14.23) запишутся:

реализации пропорционально-дифференцирующего звена используют ОУ (см.

рис. 14.3,б).

Передаточная функция пропорционально-дифференцирующего звена,

реализованного на основе ОУ, имеет вид

где k R1/R , T R C .

АФХ, ЛАЧХ и ЛФЧХ пропорционально-дифференцирующего звена,

реализованного на основе операционного усилителя, с учетом (14.27)

219

Пропорционально-дифференцирующее звено является фильтром верхних частот, так как его ЛАЧХ растет с увеличением частоты (см. рис 14.2). Поэтому введение такого звена в САР расширяет ее полосу, повышает быстродействие.

14.2.2. Пропорционально-интегрирующее звено

Идеальное пропорционально-интегрирующее (ПИ) звено имеет следующую передаточную функцию

Таким образом, пропорционально-интегрирующее звено эквивалентно последовательному соединению интегрирующего звена и пропорционально-

дифференцирующего звена. Такое звено применяется вместо простого интегрирующего звена для повышения астатизма в тех случаях, когда введение интегрирующего звена требует дополнительной коррекции для сохранения устойчивости или необходимого качества переходного процесса.

Заметим, что знак при коэффициенте k И воздействия по интегралу всегда должен быть положительным, в то время как перед коэффициентом kП

воздействия по производной он может быть любым. По частотным свойствам пропорционально-интегрирующее звено противоположно пропорционально-

дифференцирующему и является фильтром нижних частот.

АФХ, ЛАЧХ и ЛФЧХ идеального пропорционально-интегрирующего звена для положительного воздействия по производной с учетом (14.31)

соответственно запишутся:

где TПИ k П 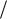k И — постоянная времени пропорционально-интегрирующего звена.

На рис 14.4,а приведены АЛАЧХ и ЛФЧХ для идеального пропорционально-интегрирующего звена.

Пропорционально-интегрирующие звенья реализуются на основе RC -

звена и на основе ОУ (рис. 14.5).

Передаточная функция пропорционально-интегрирующего звена,

реализованного на основе RC -звена, имеет вид