
Радиоавтоматика
..pdf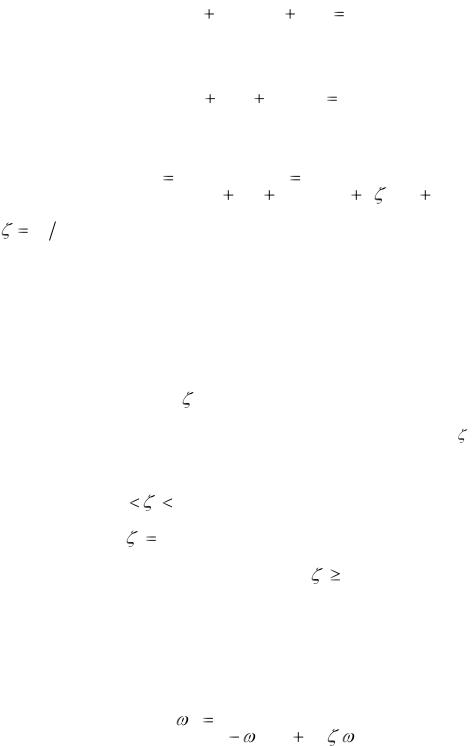
121
11.4. Апериодическое звено
второго порядка
Дифференциальное уравнение для апериодического звена второго
порядка имеет вид
T |
2 d 2 y (t) |
T |
dy (t) |
y(t) |
k x(t) . |
(11.26) |
|
|
|
|
|||||
|
|
dt 2 |
1 |
dt |
|
|
|
|
|
|
|
|
|
||
В операторной форме уравнение (11.26) запишется |
|
||||||
|
|
( T 2 p 2 |
T |
p 1) y( p) |
k x( p) . |
(11.27) |
|
|
|
|
1 |
|
|
|
|
Соответственно передаточная функция
|
W ( p) |
k |
|
|
|
k |
, |
(11.28) |
|
|
|
|
|
|
|
|
|||
|
T 2 p2 T p 1 T 2 p2 |
2 T p 1 |
|||||||
|
|
|
|
||||||
|
|
|
1 |
|
|
|
|
|
|
где |
T1 (2T ) — коэффициент |
демпфирования, или относительный |
|||||||
коэффициент затухания, причем постоянная Т «раскачивает» колебания, а T1
«демпфирует» их.
Таким образом, апериодическое звено второго порядка характеризуется тремя параметрами: коэффициентом передачи k, постоянной времени T и
коэффициентом демпфирования . |
|
|
|
|
||
В зависимости от величины коэффициента демпфирования |
различают |
|||||
типы звеньев: |
|
|
|
|
|
|
а) колебательное ( 0 |
1 ) ; |
|
|
|
|
|
б) консервативное ( |
0 ) ; |
|
|
|
|
|
в) апериодическое звено второго порядка ( |
1) . |
|
|
|||
Рассмотрим частотные характеристики апериодическое звено второго |
||||||
порядка. |
|
|
|
|
|
|
Амплитудно-фазовая характеристика запишется |
|
|||||
|
W ( j ) |
|
k |
|
. |
(11.29) |
|
|
|
|
|||
|
|
2T 2 j2 |
|
|||
|
1 |
T |
|
|||

122
Амплитудная, фазовая и логарифмическая амплитудная частотные
характеристики соответственно запишутся
|
|
W ( j |
) |
|
|
|
|
k |
|
|
|
|
, |
(11.30) |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
2T 2 )2 |
(2 |
T )2 |
||||||||
|
|
|
|
(1 |
|
|
|||||||||
( |
) |
|
arc tg [2 |
T |
(1 |
2T 2 )] , |
(11.31) |
||||||||
|
|
|
|
|
|
|
|
|
|
||||||
L( ) 20lg |
|
W ( j |
) |
|
20lg k |
20lg |
(1 |
2T 2 )2 |
(2 T )2 . (11.32) |
||||||
|
|
||||||||||||||
Проведем анализ частотных характеристик апериодического звена |
|||||||||||||||
второго порядка для коэффициента демпфирования 0.25 |
1. |
|
|||||||||||||
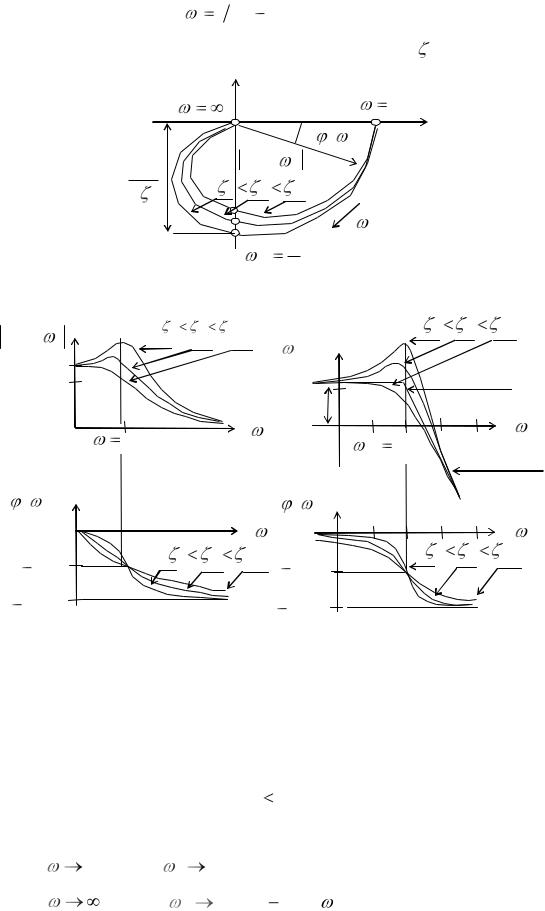
Годографы АФХ в соответствии с выражением (11.29) для апериодического звена второго порядка (рис. 11.7,а) располагаются в четвертом и третьем квадрантах, начинаются в точке k на действительной оси при частоте
0 , пересекают мнимую ось при |
с |
1 T |
в точке с координатой k 2 |
|
и при |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
стремятся к началу координат. С |
|
|
уменьшением |
характеристика |
||||||||||||||||||
деформируется, вытягиваясь вниз влево. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
По АЧХ, описываемой выражением (11.30), видно, что при частоте |
|
0 |
||||||||||||||||||||
коэффициент передачи равен k и при частоте |
равен нулю (рис. 11.7,б). |
||||||||||||||||||||||
Для |
3 |
0,707 |
коэффициент |
передачи |
убывает, |
стремясь к нулю, с |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
2 |
|
|
||
увеличением . |
Для |
0.707 |
( 1, |
2 ) АЧХ имеет на частоте |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
P |
|
T |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
максимум, |
равный |
|
W ( j P ) |
|
|
|
k |
|
|
|
, причем с уменьшением |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||
|
|
|
|
|
|
2 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
максимум увеличивается, стремясь к величине k 2 на частоте |
с |
1 T . |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Все ФЧХ, |
описываемые выражением (11.31), |
имеют на частоте |
|
|
0 |
|||||||||||||||||
фазовый сдвиг равный нулю (рис.11.7,в). С увеличением частоты сдвиг по фазе растет, стремясь к фазе минус 1800 при частоте 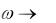 . На частоте
. На частоте 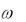 1
1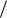 T все
T все
|
|
|
|
|
|
|
|
|
|
123 |
ФЧХ проходят через точку ( |
1 T , |
900 ). В окрестностях этой точки ФЧХ |
||||||||
идут тем круче, чем меньше коэффициент демпфирования . |
|
|
||||||||
|
|
|
jV |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) |
|
U |
|
|
|
|
|
|
W ( j |
) |
|
|
|
||
|
k |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
C |
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
W ( j |
) |
1 |
2 |
3 |
|
|
|
1 |
2 |
3 |
|
|
|
L( |
),ДБ |
|
|
|
|
||
|
k |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
АЛАЧХ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 lg k |
|
|
|
|
|
|
1/T |
|
|
|
|
C |
1/ T |
-40дБ/дек |
||
|
|
|
|
|
|
|
||||
|
|
б |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
),0 |
|
|
|
|
( ),0 |
|
г |
|
|
( |
|
|
|
|
|
|
|
|
||
|
0 |
|
|
|
|
|
|
|
|
|
900 |
1 |
2 |
3 |
|
900 |
|
1 |
2 |
3 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||
180 0 |
|
|
|
|
180 0 |
|
|
|
|
|
|
|
в |
|
|
|
|
|
д |
|
|
Рис. 11.7. Частотные характеристики апериодического звена второго порядка: а — АФХ; б — АЧХ; в — ФЧХ;
г — ЛАЧХ; д — ЛФЧХ
Рассмотрим ЛАЧХ и ЛФЧХ апериодического звена второго порядка для коэффициента демпфирования 0.25 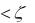 1 (рис.11.7,г,д).
1 (рис.11.7,г,д).
ЛАЧХ обладает асимптотами:
а) при |
0 — L( ) |
20 lg k ; |
б) при |
— L( ) |
20 lg k 40lg T . |

124
Последняя будет прямой с наклоном минус 40 дБ/дек, а первая —
горизонтальная прямая. Пересекаются они при сопрягающей частоте |
c |
1 T . |
||||||
Все ЛФЧХ на сопрягающей частоте имеет значение фазы ( |
с ) |
900 |
||||||
и наклонены тем круче, чем меньше коэффициент демпфирования . |
|
|||||||
На сопрягающей частоте |
c |
1 T |
отклонение |
реальной |
ЛАЧХ от |
|||
асимптотической равно |
|
|
|
|
|
|
|
|
L ( с ) L( c ) LA ( c ) |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
20 lg k 20 lg |
(1 |
2 T 2 )2 ( 2 T )2 |
20 lg k |
|
|
|||
|
|
|
|
1 |
|
|
. |
(11.33) |
|
|
20 lg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||
Для определения переходных характеристик воспользуемся выражением для операторного коэффициента передачи (11.28) и найдем корни
характеристического уравнения T 2 p2 2 |
T p 1 |
0 : |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
||
p1,2 |
|
|
|
|
. |
(11.34) |
||
T |
|
T |
|
|||||
|
|
|
|
|
|
|||
Для колебательного звена (0 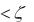 1 ) корни характеристического уравнения (11.34) получаются комплексно-сопряженными и переходная и импульсная переходная характеристики запишутся:
1 ) корни характеристического уравнения (11.34) получаются комплексно-сопряженными и переходная и импульсная переходная характеристики запишутся:
|
|
t |
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
h (t) k 1 e T |
cos |
|
|
|
|
t |
|
|
|
|
|
|
sin |
|
|
|
t , (11.35) |
|||||
|
T |
|
|
|
|
|
|
|
|
|
T |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
t |
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t . |
(11.36) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
(t ) |
|
|
|
|
|
|
e T |
sin |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
T |
|
|
|||||||||||||
|
|
|
|
T |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
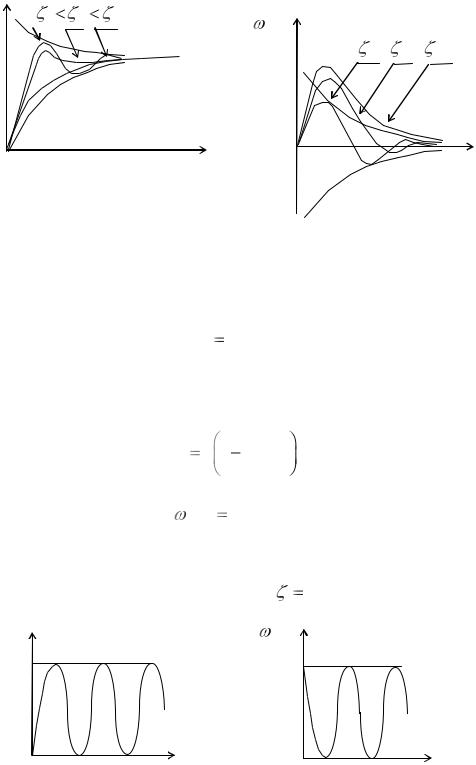
На рис. 11.8 приведены переходная и импульсная переходная |
||||||||||||||||||||||
характеристики для колебательного звена ( 0.25 |
|
|
1 ) . |
|
|
|||||||||||||||||
125
h(t) |
1 |
2 |
3 |
(t) |
|
||||
|
|
|
|
1 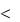 2
2 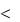 3
3
0 |
t |
0 |
|
t |
|
|
а |
б |
Рис. 11.8. Переходная (а) и импульсная переходная (б) характеристики колебательного звена
Для консервативного звена ( 0) корни характеристического уравнения
0) корни характеристического уравнения
(11.34) получаются мнимыми, тогда переходная и импульсная переходная
характеристики примут следующий вид:
h(t ) k 1 |
|
cos |
|
|
t |
|
; |
(11.37) |
|
|
T |
||||||||
|
|
|
|
|
|||||
( t ) |
k |
sin |
|
|
t |
. |
|
(11.38) |
|
|
|
|
|
|
|||||
|
T |
|
|
|
T |
|
|
||
На рис. 11.9 приведены переходная и импульсная переходная |
|||||||||
характеристики для консервативного звена ( |
0) . |
|
|||||||
h(t) |
|
|
|
|
( t ) |
|
|
||
k |
|
|
k |
|
|
||||
|
|
|
|
|
|
|
|||
|
|
|
T |
|
|
||||
а t б t
Рис. 11.9. Переходные (а) и импульсная переходная (б) характеристики консервативного звена:

|
|
|
|
|
|
126 |
Для |
апериодическое |
звено второго |
порядка |
( 1) |
и корни |
|
характеристического уравнения получаются действительными: при |
1 корни |
|||||
равны — p1 |
p2 |
1 T , при |
1 корни неравны — p1 |
p2 . |
|
|
Для |
1 |
операторный |
коэффициент |
передачи |
(11.28), |
переходная |
характеристика (11.35) и импульсная переходная характеристика (11.36)
соответственно примут вид:
W ( p) |
|
|
k |
|
|
|
|
|
|
|
k |
, |
(11.39) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
T 2 p2 |
2 T p |
1 |
(1 |
pT)2 |
|||||||||||
|
|
|
|
|
|
|
t |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
h ( t ) k (1 2 e |
T ) |
, |
|
|
|
(11.40) |
||||||||
|
|
|
|
k |
|
|
|
t |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
( t ) |
2 |
e |
|
T . |
|
|
|
|
(11.41) |
||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
||
Для 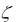 1 операторный коэффициент передачи (11.28), переходная характеристика (11.35) и импульсная переходная характеристика (11.36)
1 операторный коэффициент передачи (11.28), переходная характеристика (11.35) и импульсная переходная характеристика (11.36)
соответственно примут вид
|
W ( p) |
|
|
|
|
|
k |
|
|
|
|
|
|
, |
|
|
|
|
(11.42) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
(1 |
pT1 )(1 |
|
pT2 ) |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
T1 |
|
t |
T2 |
|
t |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
h ( t ) |
|
k (1 |
|
|
|
e |
T1 |
|
e T2 ) , |
(11.43) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
T1 |
|
T2 |
|
|
|
T1 |
|
T2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
t |
|
|
|
|
|||||
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( t ) |
|
|
|
|
( e |
T1 e |
T2 ) |
, |
|
|
(11.44) |
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
T1 |
|
T2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где T1,2 T ( |
2 |
1 ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
На рис. 11.10 приведены частотные и переходные характеристики |
|||||||||||||||||||||||
апериодического звена второго порядка для |
1. |
|
|
|
|
|
|
|
|
|
|||||||||||||
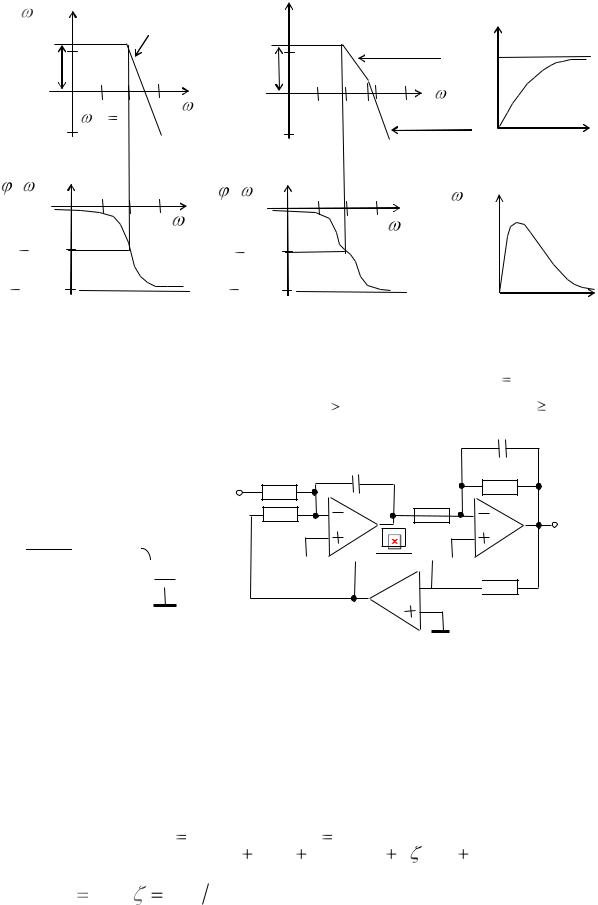
Принципиальные схемы апериодического звена второго порядка реализуются на основе RLC-звена и операционных усилителей (рис. 11.11).
127
L( ), ДБ |
|
-40дБ/дек |
L(ω), ДБ |
|
|
|
|
|
||||||
|
|
|
|
|
|
h(t) |
|
|||||||
|
|
|
|
|
-20дБ/дек |
|
||||||||
20 lg k |
|
|
|
|
|
|
|
20 lg k |
|
k |
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
1 |
1 |
-40дБ/дек |
|
|||
|
|
|
|
|
|
|
|
|
||||||
|
C |
1/ T |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
T1 |
|
T2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
t |
|||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
( ) , 0 |
( |
) , |
0 |
( t ) |
|
|
|
|
|||
900 |
|
90 0 |
|
|
|
180 0 |
|
180 0 |
0 |
|
|
|
|
|
|
t |
|
|
а |
|
|
|
|
|
|
б |
|
в |
|
Рис. 11.10. Характеристики апериодического звена второго порядка: а — АЛАЧХ и АЛФЧХ для 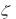 1 ;
1 ;
б — АЛАЧХ и АЛФЧХ для 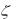 1 ; в — ПХ и ИПХ для
1 ; в — ПХ и ИПХ для 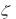 1
1
x(p) |
R |
C |
R3 C1 |
|
|
R2 |
|
|
|
|
y(p)
R |
L |
y(p) |
R |
|
|



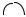
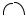





 R4 x(p) C
R4 x(p) C 



а |
б |
|
|
Рис. 11.11. Принципиальные схемы апериодического звена |
|
второго порядка: а — на основе RLC-звена; б — на основе ОУ |
|
Операторный коэффициент передачи апериодического звена второго
порядка на основе RLC-звена запишется
|
|
W ( p) |
1 |
|
|
k |
, |
(11.45) |
|
|
|
|
|
|
|
|
|||
|
|
p2 LC pRC 1 |
T 2 p2 |
2 T p 1 |
|||||
|
|
|
|
|
|||||
где T 2 |
LC; |
RC ( 2T ) . |
|
|
|
|
|
||

128
Операторный коэффициент передачи апериодического звена второго порядка на основе операционного усилителя запишется
|
W ( p) |
|
k |
|
|
, |
(11.46) |
|
|
|
|
|
|
||||
|
T 2 p2 2 |
|
|
|||||
|
|
|
T p 1 |
|
||||
|
|
|
|
|
|
|
||
где k R1 R4 ; T |
|
R2 K0 ; 1 / (2 |
T2 K0 ); |
|
||||
T2 R3 C1; K0 R3 R1 / (R C R2 R3) .
11.5. Интегрирующее звено
Дифференциальное уравнение для интегрирующего звена запишется
y(t) |
k |
x(t)dt . |
(11.47) |
||||||||||
В операторной форме уравнение (11.47) примет вид |
|
||||||||||||
y( p) |
(k / p) x( p) . |
(11.48) |
|||||||||||
Соответственно передаточная функция |
|
||||||||||||
|
|
W ( p) |
k |
. |
|
|
(11.49) |
||||||
|
|
||||||||||||
|
|
|
|
|
|
|
p |
|
|||||
Амплитудно-фазовая характеристика |
|
|
|
|
|
|
|
||||||
|
|
W ( j |
) |
|
|
|
j |
k |
. |
(11.50) |
|||
|
|
|
|||||||||||
Амплитудная, фазовая и логарифмическая амплитудная частотные |
|||||||||||||
характеристики соответственно запишутся: |
|
|
|
|
|
|
|
||||||
|
|
W ( j |
|
) |
|
|
|
k |
, |
(11.51) |
|||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
||||||||
( |
) |
|
|
|
900 , |
|
|
(11.52) |
|||||
|
|
|
|
|
|
|
|||||||
L ( ) 20 lg |
W ( j |
) |
|
|
|
20 lg k 20 lg . |
(11.53) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При поступлении на вход интегрирующего звена единичного ступенчатого воздействия x(t)=1(t) для изображения выходной величины с учетом формулы (11.49) получим
|
|
|
|
|
|
|
|
|
|
|
|
|
129 |
||||
|
|
|
|
y ( p) W ( p ) |
1 |
|
k |
|
, |
(11.54) |
|||||||
|
|
|
|
p |
p2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Тогда для переходной и импульсной переходной характеристик запишем: |
|||||||||||||||||
|
|
|
h ( t ) |
L 1{k |
|
p 2 } |
k t . |
|
(11.55) |
||||||||
|
|
|
|
( t ) |
h (t) |
k . |
|
|
|
(11.56) |
|||||||
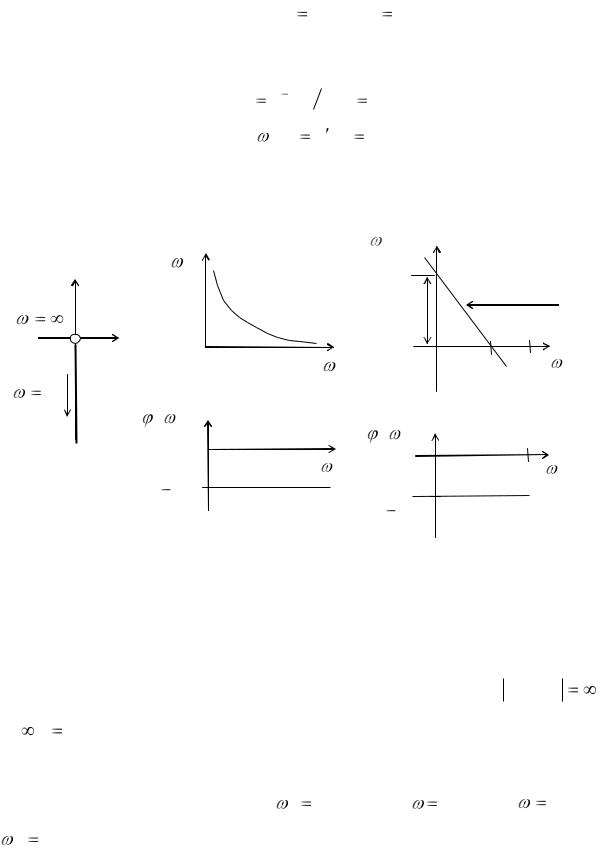
Рассмотрим частотные |
характеристики |
интегрирующего звена |
|||||||||||||||
(рис. 11.12). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L( ), ДБ |
|
|
|
|
|
|
||||
jV |
W ( j |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-20дБ/дек |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
20 lg k |
|
|
|
|
|
|
|||
U |
|
|
б |
|
|
|
|
|
|
|
1 |
k 10 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
) , 0 |
|
|
|
|
|
|
|
|
|
г |
||||||
( |
|
|
|
|
( |
) , 0 |
|
|
|
|
|
|
|||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||
а |
|
|
|
|
|
|
|
|
1 |
10 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
90 0 |
|
|
|
|
|
|
90 0 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
в |
|
|
|
|
|
|
д |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Рис. 11.12. Частотные характеристики интегрирующего звена: а — АФХ; б — АЧХ; в — ФЧХ; г — ЛАЧХ; д — ЛФЧХ.
АФХ (рис. 11.12,а) совпадает с отрицательной мнимой полуосью. |
|
АЧХ (рис. 11.12,б) — гипербола с асимптотами W ( j0) |
и |
W ( j |
) |
0 . |
|
|
|
ФЧХ (рис. 11.12,в) — постоянная величина, равная минус 900 . |
|
||
|
Из выражения (11.53) для L( ) 0 получим |
k и при |
1 найдем |
|
L( ) |
20 lg k . |
|
|
|
130
Таким образом, ЛАЧХ интегрирующего звена (рис. 11.12,г) — прямая с
наклоном минус 20дБ/дек, проходящая через точку с абсциссой |
1 и |
||
ординатой 20 lg k и пересекающая ось частот при |
k . |
|
|
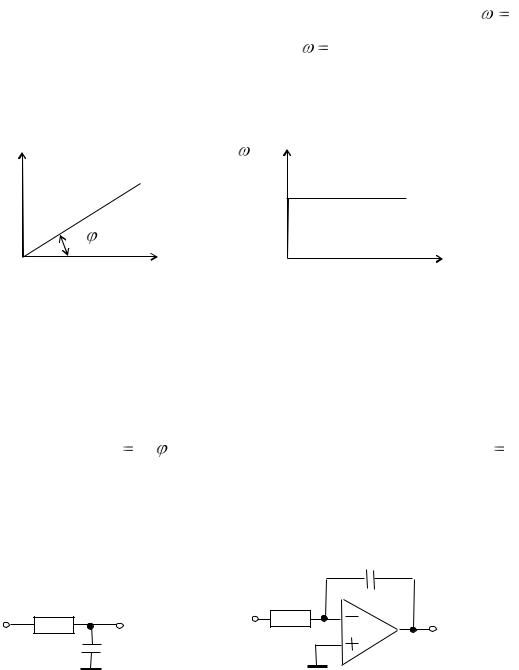
Перейдем к переходным |
характеристикам |
интегрирующего |
звена |
(рис. 11.13).
h(t) |
( t ) |
|
|
|
k |
0 |
t |
0 |
t |
|
|
||
|
а |
|
б |
Рис. 11.13. Переходные характеристики интегрирующего звена: а — ПХ; б — ИПХ.
ПХ (рис. 11.13,а) — прямая линия, выходящая из начала координат, с
угловым коэффициентом k tg при постоянной входной величине y(t) 1(t) .
ИПХ (рис. 11.13,б) — постоянная величина, равная k.
Принципиальные схемы интегрирующего звена реализуются на основе
RC-звена и операционного усилителя (рис. 11.14). |
|
|||
|
R |
|
R |
C |
x(p) |
C |
y(p) |
x(p) |
y(p) |
|
|
|
|
|
|
а |
|
|
б |
Рис. 11.14. Принципиальные схемы интегрирующего звена: а — на основе RC-звена; б — на основе ОУ
Операторные коэффициенты передачи для интегрирующего звена,
реализованного на основе RC-звена и на основе ОУ, соответственно запишутся:
