
- •ГЛАВА 7. ОСНОВЫ АЛГОРИТМИЗАЦИИ
- •1. ПОНЯТИЕ ОБ АЛГОРИТМЕ
- •2. ОСНОВНЫЕ СТРУКТУРЫ
- •2.1. Структура «следование»
- •2.2. Структура «развилка»
- •2.3. Структура «цикл»
- •3. ОСНОВНЫЕ ТИПЫ АЛГОРИТМОВ
- •3.1. Линейный алгоритм
- •3.2. Разветвленный алгоритм
- •3.3. Циклический алгоритм
- •Практические задания
- •1. Алгоритмы линейной структуры
- •2. Алгоритмы разветвляющейся структуры
- •3. Алгоритмы циклической структуры (цикл «ПОКА»)
- •4. Алгоритмы циклической структуры (цикл «ДО»)
- •ГЛАВА 8. ОСНОВЫ ПРОГРАММИРОВАНИЯ В СРЕДЕ VISUAL С++ 2005
- •ВВЕДЕНИЕ
- •1. РАЗРАБОТКА ПРОГРАММЫ
- •2. ПЕРЕМЕННЫЕ
- •3. ЛИНЕЙНАЯ ПРОГРАММА
- •3.1. Оформление линейной программы
- •3.2. Программирование в стандартизованной среде CLR
- •Практические задания
- •Русская система мер
- •4. ПРОГРАММА С ВЕТВЛЕНИЕМ
- •Практические задания
- •5. ЦИКЛ С ПАРАМЕТРОМ
- •6. ЦИКЛ «ПОКА»
- •Практические задания
- •7. ОДНОМЕРНЫЕ МАССИВЫ
- •7.1. Понятие об одномерном массиве
- •7.2. Сортировка в одномерном массиве
- •Практические задания
- •8. ДВУМЕРНЫЕ МАССИВЫ
- •8.1. Понятие о двумерном массиве
- •8.2. Датчик случайных чисел
- •Практические задания
- •9. ФУНКЦИИ
- •9.1. Понятие о пользовательских функциях
- •Рис. 8.20. Пятиугольник со сторонами a, b, c, d, f и диагоналями h,g.
- •9.2. Рекурсия
- •9.3. Вызов функции из функции
- •9.4. Функция типа void и глобальные переменные
- •9.5. Передача в функцию имени функции
- •Практические задания
- •10. СОБСТВЕННАЯ БИБЛИОТЕКА ПРОГРАММИСТА
- •10.1. Перегрузка функций
- •Рис. 8.25. Результат работы программы примера
- •11. ПЕРЕЧИСЛИМЫЙ ТИП
- •11.1. Понятие о перечислимом типе
- •11.2. Множественный выбор
- •12. УКАЗАТЕЛИ
- •12.1. Понятие об указателях
- •12.2. Указатели и функции
- •12.3. Указатели и динамические массивы
- •12.4. Указатели и перегрузка операций
- •13. ОБРАБОТКА СИМВОЛЬНЫХ СТРОК
- •13.1. Символьные переменные
- •13.2. Символьные строки (как массивы символов)
- •13.3. Обработка массивов строк
- •Практические задания
- •14. СТРУКТУРЫ
- •Практические задания
- •15. КЛАССЫ
- •15.1. Понятие класса
- •15.2. Открытые и закрытые члены класса
- •15.3. Конструкторы и деструкторы
- •Практические задания
- •Раздел А
- •Раздел Б
- •16. ФАЙЛЫ
- •16.1. Работа с текстовыми файлами
- •16.2. Работа со структурами в файлах
- •16.3. Работа с классами в файлах
- •Практические задания
- •Раздел А
- •Раздел Б
- •ПРИЛОЖЕНИЯ
- •Приложение 1. Список библиотечных функций
- •Математические функции
- •Строковые функции (для работы с символьными массивами)
- •Приложение 2. План лабораторных работ
- •ГЛАВА 9. ПРИЛОЖЕНИЯ WINDOWS FORMS
- •ВВЕДЕНИЕ
- •1. РАЗРАБОТКА ПРИЛОЖЕНИЯ
- •3. ДИНАМИЧЕСКИЕ ССЫЛКИ НА ОБЪЕКТЫ
- •3.1 Понятие о динамических ссылках.
- •3.2. Программа «Калькулятор»
- •4. ИСПОЛЬЗОВАНИЕ ТАЙМЕРА. КОМПОНЕНТ CHECKBOX
- •4.1 Таймер
- •4.2. Компонент CheckBox
- •5. СПИСКИ ВЫБОРА И ПОЛОСЫ ПРОКРУТКИ. ГРАФИЧЕСКИЕ КОМПОНЕНТЫ В C++Builder
- •5.1. Список выбора ListBox
- •5.2. Полосы прокрутки
- •5.3. Графика
- •6. РАБОТА С ТЕКСТОВЫМИ ФАЙЛАМИ.
- •6.1. Чтение и запись текстового файла
- •ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
- •Раздел 1. Кнопки, метки и окна редактирования
- •Раздел 2. Радиокнопки
- •Раздел 3. Полосы прокрутки
- •Раздел 4. Обработка текстовых файлов
- •ЛИТЕРАТУРА
- •ТЕСТЫ
- •Тесты по основам алгоритмизации
- •Тесты по программированию на С++
- •Учебное издание
46
В пяти следующих заданиях условие одинаковое: для задан-
ного натурального числа n рассчитать сумму и сравнить со значением y :
5.21. |
1- |
1 |
+ |
|
1 |
- |
1 |
+... |
+ |
(-1)n-1 |
|
+... |
|
y = π/4 |
||||||||||||||||||||
3 |
5 |
7 |
2n -1 |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
5.22. |
|
1 |
|
|
|
+ |
|
|
|
1 |
|
|
+ |
1 |
+...+ |
1 |
|
+... y = 0,5 – π/8 |
||||||||||||||||
3*5 |
7*9 |
|
|
|
|
(4n -1)(4n +1) |
||||||||||||||||||||||||||||
|
|
|
|
|
11*13 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
5.23. 1+ |
1 |
|
+ |
1 |
|
+ |
1 |
|
+...+ |
1 |
+... |
|
y = π2/6 |
|||||||||||||||||||||
2 |
|
2 |
2 |
|
2 |
|||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
4 |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|||||||
5.24. |
1+ |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = 4/ π |
||||||
|
|
|
|
|
|
|
|
|
|
|
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
2 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
52 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
2 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
2 + |
|
72 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+... |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||
5.25. |
2*2*4*4*6*6*8*8*...*2n*2n |
|
y = π/2 |
|||||||||||||||||||||||||||||||
1*3*3*5*5*7*7*9*...*(2n -1) |
||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
6.ЦИКЛ «ПОКА»
ВС++ имеется также струк-
тура повторения While, которая служит для организации цикла «ПОКА»:
While (условие) тело цикла
Работает он так: тело цикла повторяется, пока заданное условие остается истинным.
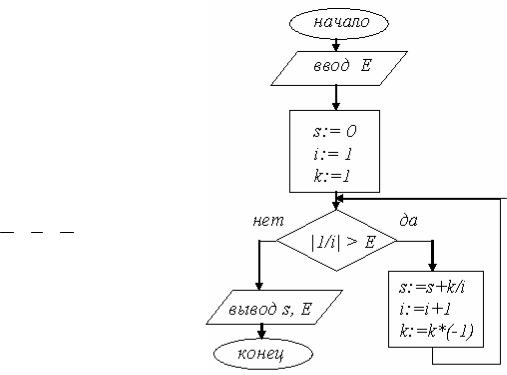
Пример 6.1. Рассчитать сум-
му вида: 1- 1 + 1 - 1 +... с задан- 2 3 4
ной точностью Е.
Иначе говоря, проводить суммирование, пока очередное слагаемое является большимЕ (по абсолютной величине).
47
//сумма бесконечного ряда
#include <iostream> #include <windows.h> using namespace std; int main()
{int i,k; double s,e; char str[256], str1[256];
AnsiToOem("введи точность \n", str); cout<<str; cin>>e;
s=0; i=1; k=1;
AnsiToOem(" сумма = ", str); AnsiToOem(" с точностью ",str1); while(1.0/i>e){s=s+(double)k/i; i++; k=k*(-1);}; cout<<str<<s<<str1<<e<<"\n";
return 0;}
В данной программе использован известный нам алгоритм суммирования. Суть его в том, что вводится переменная (здесь это переменная s), задается ей нулевое значение, а затем в нее накапливается сумма. Очередное слагаемое – обратное к очередному числу натурального ряда. Однако четные (по номеру) слагаемые идут со знаком «минус», нечетные – со знаком «плюс». Для учета этого зна-
ка введена дополнительная переменнаяk, которая последовательно принимает значение то +1, то –1. Переменная i последовательно дает очередное натуральное число(2, 3, 4 и т.д.). Для удобства она описана как целая (int).
Расчет по этой программе приЕ = 0,1 дает значение 0,6456349, а точное значение для такой суммы (оказывается у этой бесконечной суммы результат – конечное число!) есть ln(2) = 0,6931...
Обратите внимание, что нам здесь потребовалось произвести в программе преобразование типов (целый к типу double при выполнении суммы), иначе в результате деления целого на целое получался нуль! И в условии, задающем цикл, мы сделали явное преобразование целого к вещественному – записав вместо целой единицы вещественную единицу (1.0).
Для изменения порядка работы в цикле в языке ++С применяются два оператора: break (для досрочного прерывания цикла) и continue – для пропуска следующих за ним операций с переходом в конец цикла, но из цикла выхода не производится.
Пример 6.2. Среди К первых членов последовательности вида: 1, 1+1/2, 1+1/2+1/3, ... найти первый, больший заданного числа А. Если же его нет (среди первых К членов), то напечатать об этом сообщение.

48
//поиск члена последовательности, меньшего //заданного числа a
#include <iostream> #include <windows.h> using namespace std; int main()
{int i,k; double a,s;
char str[256],str1[256],str2[256]; AnsiToOem("введи количество \n",str);
cout<<str; cin>>k;
AnsiToOem("введи число a \n",str); cout<<str; cin>>a;
s=0; i=1;
while (i<=k) { s=s+1.0/i; if (s>a) break ; i++;}; AnsiToOem(" такого числа нет \n", str); AnsiToOem(" при i =", str1);
AnsiToOem(" большее а число ",str2); if (i>k) cout<<str;
else cout<<str1<<i<<str2<<s<<"\n"; return 0;}
Практические задания
6.1. Вычислить для заданногоx сумму вида: x – x2/2 + x3/3 –
– x4/4 +... с заданной точностьюЕ (когда очередное слагаемое по модулю станет меньше Е, то суммирование прекратить). Результат сравнить с величиной y = ln(x + 1), x > 0.
6.2. Для заданного Х в последовательности вида: sinX, sin(sinX)), sin(sin(sinX)), ... найти первое число, меньшее по модулю 0,01.
6.3. Найти наименьший номер n, для которого выполняется ус-
ловие | an |
– a n–1| < 0,1 , если |
последовательность an |
имеет |
вид: |
|||||||
a n+1 = an + 2/an a1 = 1. |
|
1 |
|
1 |
|
|
1 |
|
|
||
6.4. C |
заданной точностью |
Е рассчитать: 1+ |
+ |
+ |
+... |
Ре- |
|||||
|
|
|
|||||||||
|
|
1! |
2! |
3! |
|
||||||
зультат сравнить со значением e = 2,718281828... Напомним, что запись вида n! означает 1×2×3×...×n (последовательное произведение целых чисел от 1 до n). Указание. Для вычисления значенияn! применить рекуррентную формулу: n! = (n – 1)! × n.
6.5. Для заданного x c заданной точностью E рассчитать сумму
вида: x - x3 + x5 - x7 +...Результат сравнить со значением y = sin x.
3! 5! 7!
49
6.6 Для заданного x с заданной точностью E рассчитать сумму
вида: 1- x2 + x4 - x6 +... Результат сравнить со значением y = cos x.
2! 4! 6!
В приведенных ниже заданиях рассмотреть указанную последовательность в цикле и выйти из цикла, достигнув указанного условия с выдачей порядкового номера члена, при котором достигнуто условие. Если же за m оборотов цикла условие не достигнуто, напечатать об этом сообщение.
6.7. |
a |
n+1 |
=tga |
n |
/2, a =0,1 |
|
| a |
n |
|<10-3 |
|
|
|||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||
6.8. |
an = 2n /n!, |
| an |<10-8 |
|
|
|
|
|
|
||||||||||
6.9. a =1/ n |
|
|
| a |<0,1 |
|
|
|
|
|
|
|||||||||
n!, |
|
|
|
|
|
|
||||||||||||
6.10. |
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|<10-4 |
||
|
a |
n+1 |
=(a |
n |
+1/a |
n |
)/2, |
a |
=10, |1-a |
n |
||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||
6.11. |
an+1 =1,99an -an-1, |
a1 =1,a2 =1, |
an <0,9 |
|||||||||||||
6.12. |
a |
n+1 |
= |
(a |
n |
+ a |
n-1 |
)/2, |
a |
=1,a |
=10, |
| a |
n |
-7 |<10-4 |
||
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|||||
6.13. |
a |
|
= |
|
|
|
, |
a =0, |
| a |
-a |
|<10-3 |
|||||
n+1 |
|
2 + a |
|
|||||||||||||
|
|
|
|
|
|
n |
|
1 |
|
n |
n-1 |
|
|
|
||
6.14. Написать программу, вычисляющую сумму и среднее арифметическое последовательности положительных чисел, которые вводятся с клавиатуры(длина последовательности не ограничена). Для завершения ввода нужно нажать 0.
6.15. Написать программу, которая определяет максимальное
число |
из |
введенной |
последовательности |
положительных |
чисел |
|
(длина последовательности не ограничена). Для завершения ввода |
||||||
нужно нажать 0. |
|
|
|
|||
6.16. |
Написать программу, которая определяет минимальное |
|||||
число |
из |
введенной |
последовательности |
положительных |
чисел |
|
(длина последовательности не ограничена). Для завершения ввода |
||||||
нужно нажать 0. |
|
|
|
|||
6.17. |
Написать программу, которая задумывает число в диапа- |
|||||
зоне от 1 до 10 и предлагает пользователю угадать число за 5 попы- |
||||||
ток. В завершение должно быть сообщение о том, что пользователь |
||||||
угадал число или нет. |
|
|
|
|||
6.18. |
Написать программу, которая выводит на экран таблицу |
|||||
значений функции y= 2x2 – 5x – 8 в диапазоне от – 4 до 4. Шаг изменения аргумента 0,5
6.19. Написать программу, которая вычисляет наибольший общий делитель двух целых чисел.
50
6.20. Написать программу для вычисления сопротивления цепи из нескольких проводников, соединенных последовательно (значения сопротивлений вводятся одно за другим и для завершения ввода нажимается 0).
6.21. Написать программу для вычисления сопротивления цепи из нескольких проводников, соединенных параллельно (значения
сопротивлений вводятся одно за другим и для завершения ввода нажимается 0).
6.22. Написать программу, которая выводит на экран таблицу значений функции y= 1/x в диапазоне от заданного А(вводится извне) и до 0. Шаг изменения аргумента h также вводится извне.
6.23. Написать программу, которая вычисляет число π с заданной пользователем точностью. Для этого суммируют последовательность: 1 – 1/3 + 1/5 – 1/7 + 1/9 – … до тех пор, пока очередное слагаемое (по абсолютной величине) не станет меньше заданной точности. Полученная сумма дает примерное значение числа π/4, т.е умножая полученную сумму на 4 и получим π.
6.24 Написать программу вычисления значения квадратного корня из числа a>0 с заданной точностью E на основе соотношения
x |
= |
xn + a/ x n |
n =1,2,3,... |
|
|||
n+1 |
2 |
|
|
|
|
||
где xn – предыдущее, xn+1 – последующее приближение к корню. Начальное приближение для определенности положить равнымa/2. Точность вычислений считается достигнутой, когда | xn+1 – xn |<E
6.25 Спортсмен в первый день пробежал 10 км. Каждый следующий день он увеличивал дневную норму на 10 % от нормы предыдущего дня. Определить через сколько дней спортсмен:
а) будет пробегать более 20 км; б) пробежит суммарный путь более 100 км.
