Антенны

S

Подчеркнем, что КИП не зависит от формы ДН элемента раскрыва, поэтому вместо компоненты Ex плоской волны может стоять любая функ-

ция распределения возбуждения I(x, y).

Раскрыв прямоугольной формы

Рассмотрим раскрыв прямоугольной формы размером a ×b с разде-

ляющимся АФР, т.е. I&(x, y) = I&(x)× I&(y). Такое распределение обычно и реализуется в антенных системах. Подставив в (2.36), получим

В (2.44) каждый из сомножителей по форме совпадает с множителем направленности ЛНС. В случае синфазного равноамплитудного распределения I(x) = I(y) = const сразу находим

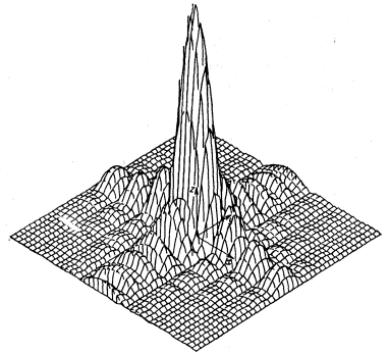
делить видимую область, границы которой соответствуют θ = ±π2, т.е. предельному случаю излучения вдоль плоскости раскрыва. С увеличением размеров раскрыва в видимую область попадает все большее число боковых лепестков. В качестве примера на рис. 2.14 приведен рельеф МН прямоугольного раскрыва. Обычно его рассматривают в двух главных плоскостях xoz и yoz , где он совпадает с МН соответствующих ЛНС. Поэтому все полученные для них результаты можно перенести на апертурные излучатели, естественно с учетом соответствия АФР. Некоторое отличие будет в КНД. Например, для синфазного раскрыва с постоянной амплитудой имеем

51

Рис. 2.14. Рельеф множителя направленности прямоугольного синфазного раскрыва

где согласно формуле (2.8) Dx и Dy – КНД эквивалентных ЛНС с размерами

и b >> λ ; число π можно рассматривать как эквивалентный КНД элемента раскрыва, близкий по значению к КНД элемента Гюйгенса, который равен 3,0.

Положением максимума ДН в пространстве можно управлять, создавая линейно изменяющееся фазовое распределение возбуждения. Зададим в плоском прямоугольном раскрыве АФР в виде суперпозиции двух бегущих волн с одинаковой амплитудой

Фактически эту суперпозицию можно рассматривать как одну бегущую волну, распространяющуюся в плоскости раскрыва в направлении ϕ = arctg(ξy ξx ) и представленной в виде проекции на оси декартовой сис-

темы координат. Подставив (2.47) в (2.36), для множителя направленности после интегрирования получим выражение (2.45), но в котором

В случае синфазного распределения было ξx = ξy = 0 .

52

Направление главного максимума излучения находится из условия

лучения в направлении θ0 ,ϕ0 . Эта формула справедлива для любой формы раскрыва и произвольного амплитудного распределения. При отклонении луча ДН от нормали к раскрыву, например при сканировании, происходит уменьшение КНД по сравнению с КНД при синфазном раскрыве (θ0 = 0) по ,,закону косинуса”

где S эф – эффективная площадь синфазного раскрыва с произвольным ам-

плитудным распределением.

Синфазный раскрыв круглой формы

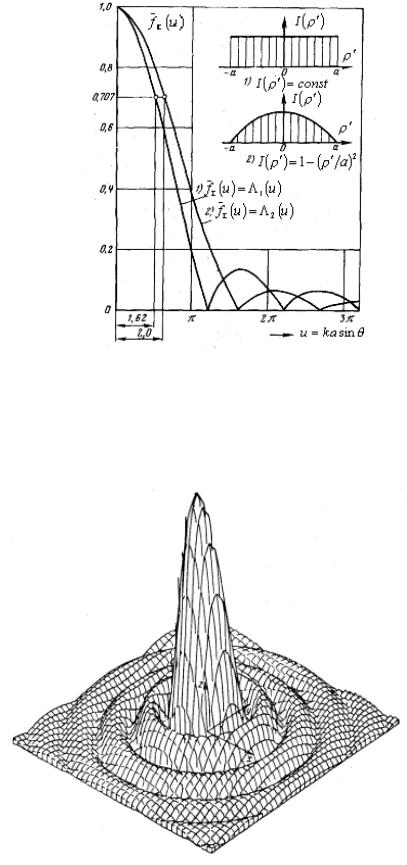
Для получения узких ДН широко используются антенны с круглым синфазным раскрывом радиуса а >> λ и амплитудным распределением поля в раскрыве I (ρ′), близким к осесимметричному. К ним относятся параболические зеркальные антенны, линзовые, конические рупорные антенны.

Рассмотрим множитель системы такого раскрыва. Введя на раскрыве полярную систему координат (ρ′, ϕ') и учитывая, что dS =ρ′ dρ′ dϕ', можем записать

Поскольку в синфазном случае множитель направленности системы не зави-

Используя интегральное представление функции Бесселя

53

Для остронаправленных антенн с большими раскрывами в пределах ширины ДН можно считать, что u << 1 и J 0 (uρ1 ) ≈ 1 .

Как уже отмечалось, для снижения уровня боковых лепестков исполь-

максимального значения в центре, равного единице, то интеграл (2.53) вычисляется и равен

функцией порядка n.

В табл. 2.1 приведены параметры и характеристики излучения прямоугольного и круглого синфазных раскрывов для разных амплитудных распределений. В табл. 2.1 введено обозначение = (1-δ ) – уровень поля на краю апертуры. На рис. 2.15 показан множитель направленности круглого синфазного раскрыва для двух видов амплитудных распределений. На рис. 2.16 изображен рельеф множителя направленности этого раскрыва.

55

Рис. 2.15. Множитель направленности круглого синфазного раскрыва при постоянном (1) и полностью спадающем к краю (2) амплитудных распределениях

Рис. 2.16. Рельеф множителя направленности круглого синфазного раскрыва

56

Вопросы для самоконтроля

Элементы общей теории антенн

1.Понятие множителя направленности ЛНС и её элемента.

2.Понятие множителя направленности ЛДС и её элемента.

3.Понятие множителя направленности плоской апертуры и её элемента.

4.Как определяется угол максимума излучения ЛНС бегущей волны?

5.Понятие оптимального режима в ЛНС.

6.Влияние на ДН формы амплитудного распределения в синфазной ЛНС.

7.Влияние на ДН линейных и кубических фазовых искажений в ЛНС с постоянным амплитудным распределением.

8.Влияние на ДН квадратичных фазовых искажений в ЛНС с постоянным амплитудным распределением.

9.Сравнить и прокомментировать множители направленности ЛНС и ЛДС.

57

3.Линейные антенны

Клинейным антеннам (ЛА) относят излучающие системы, малых по сравнению с длиной волны поперечных размеров, в которых направление протекания тока совпадает с осью системы. По характеру распределения тока ЛА можно разделить на два типа: антенны стоячих волн (АСВ) и антенны бегущих волн (АБВ). К первому типу относятся, например, вибраторные и щелевые антенны, а ко второму – спиральные антенны и диэлектрические стержневые.

3.1.Характеристики электрических вибраторов

Электрическим вибратором называется излучатель электромагнитных волн в виде линейного цилиндрического проводника радиуса а с длиной плеч l1 и l2, между внутренними торцами которых, т.е. в зазоре, приложена постоянная ЭДС. Ось z направлена вдоль оси вибратора и имеет начало в зазоре. Вибраторы могут быть симметричными, если l1 = l2 = l, и несимметричными в виде штыря высотой h ≤ λ / 4, установленного над экраном (землей). Возбуждение симметричных вибраторов осуществляется симметричным фидером (противофазной двухпроводной линией) или через симметрирующее устройство несимметричным фидером (коаксиальной линией). Вибраторы широко применяются как в качестве самостоятельных антенн, так и в сложных антенных системах; являются, например, элементами антенных решеток или облучателями зеркальных и линзовых антенн. В последних случаях для получения однонаправленного излучения они используются вместе с рефлектором. Наибольшее распространение вибраторные антенны получили в КВ и УКВ диапазонах.

Распределение тока, эффективная длина

Вследствие того, что постоянная ЭДС приложена вдоль оси вибратора между его внутренними торцами и вибратор предполагается тонким, элек-

трический ток имеет только одну составляющую I z ( z ) . При теоретическом

анализе в цилиндрической системе координат ρ, ϕ, z сначала решают внутреннюю задачу теории антенн, т.е. находят распределение тока на вибраторе. Это распределение в пространстве создает электромагнитное поле, которое можно описать одной продольной составляющей электрического потенциала

58

Выразив Ez через Azэ по известной из электродинамике формуле и подставив в граничные условия на поверхности вибратора, для эквивалентного тока получим интегральное уравнение

z

из условия обращения распределения тока в ноль на концах вибратора. Точное решение уравнения (3.2) в аналитическом виде не находится.

Его приближенное решение для симметричного вибратора имеет простой вид

где I0 = const – амплитуда тока в точке питания ( z = 0 ); верхний знак берет-

ся для z < 0, нижний – для z > 0.

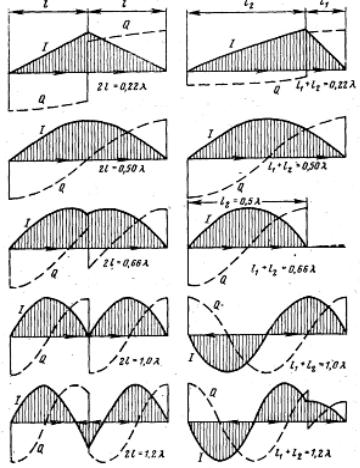
Распределения тока и заряда для тонкого симметричного вибратора приведены на рис. 3.1. При 2l ≤ λ распределение является синфазным, а при 2l > λ – переменно-фазным.

Рис. 3.1. Распределения тока и заряда в электрическом вибраторе