
Электродинамика сплошных сред
..pdf
41
4.3Электромагнитные волны в кристаллах [4, 6, 9, 14, 15]
4.3.1 Классификация кристаллов по их электромагнитным свойствам
Когда речь идет о распространении электромагнитных волн в кристалле, чаще всего говорят о его оптических свойствах.
Оптические свойства кристалла зависят в первую очередь от симметрии его диэлектрического тензора. В кристалле кубической симметрии диагональные элементы тензора равны друг другу, остальные обращаются в нуль. Поэтому в отношении своих оптических свойств кубические кристаллы вообще не отличаются от изотропных тел.
Для кубических кристаллов тензор диэлектрической проницаемости
|
|
0 |
0 |
|
|
||
|
|
|
|
|
|
|
|
0 |
|
0 |
. |
(4.15) |
|||
|
|
0 |
0 |
|
|
|
|
|
|
|
|
||||
Для одноосных кристаллов |
|
|
|
|
|||
|
1 |
0 |
0 |
|
|
||
|
|
|
|
|
|
|
|
0 |
2 |
0 |
. |
(4.16) |
|||
|
|
0 |
0 |
3 |
|
|
|
|
|
|
|
||||
Рассмотрим распространение |
электромагнитных |
волн в одноосных |
|||||
кристаллах.
4.3.2Электромагнитные волны в одноосных кристаллах
Рассмотрим немагнитный кристалл. Уравнения Максвелла для комплексных амплитуд.
|
. |
|
. |
|
|
rot H m j Em , |
(4.17) |
||||
. |
. |
|
|||
|
|
||||
rot Em j 0 H m .
Заменим векторные уравнения скалярными, при этом будем полагать, что плоская электромагнитная волна распространяется вдоль Z, т.е. (4.15) положим
|
|
|
|
|
|
|
|
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
x |
y |
|
|
|
|
|
|
|
|
||||
|
H |
my |
|
|
|
|
|
E |
|
|
|
|
|
|||
|
|
j 1Emx ; |
|
my |
j 0 Hmx |
; |
|
|||||||||
|
|
|
z |
|
||||||||||||
|
z |
|
|
|
|
|
|
|
|
(4.18) |
||||||
|
Hmx |
|
|
|
|
|
Emx |
|
|
|
|
|
||||
|
j E ; |
j |
H |
|
. |
|
||||||||||
|
|
|
|
|||||||||||||
|
z |
2 |
my |
|
z |
0 |
|
my |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||
42
|
. |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
Пусть |
Em (x0 E |
y E |
) e jkz ; |
H m (x0 H |
0 x |
y |
H |
0 y |
) e jkz ; |
||||||||||
|
|
|
|
0 x |
|
|
0 0 y |
|
|
|
|
|
0 |
|
|
||||
(4.19)
Подставим проекций из (4.19) в (4.18). Получим новую систему уравне-
ний:
kH0 y |
1E0 x ; |
kE0 y |
0 H0 x |
; |
|
|
(4.20) |
|||||||
|
|
E |
|
|
|
|
|
|
|
|
|
|
||
kH |
0 x |
; |
kE |
|
H |
|
. |
|
|
|
||||
|
2 0 y |
|
0 x |
|
0 |
|
|
0 y |
|
|
|
|||
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
0 H |
0 x |
; |
|
E |
0 H |
0 y |
. |
|||
|
|
|
0 y |
|
|
k |
|
|
0 x |
k |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Этот результат подставляем в (4.20) и после сокращений получим
k2 2 ; |
k2 2 |
. |
(4.21) |
|
1 |
0 |
2 |
0 |
|
Это дисперсионные соотношения, устанавливающие связь волнового числа с частотой и макроскопическими параметрами среды.
|
|
|
|
|
|
|
k1 1 0 , |
k2 2 0 . |
(4.22) |
||||
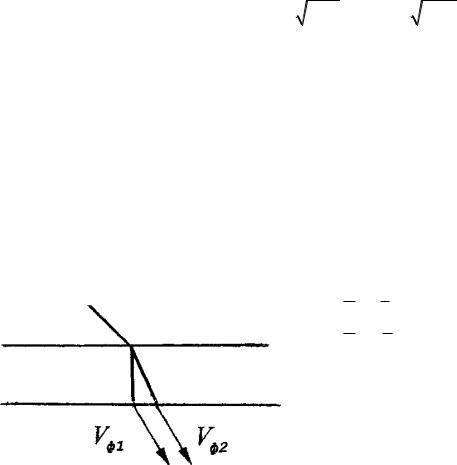
Из (4.20) находим два разных значения фазовой скорости
V |
, |
V |
. |
(4.23) |
Ô1 |
k1 |
Ô 2 |
k2 |
|
|
|
|
Если вдоль оси Z одноосного кристалла распространяется плоская электромагнитная волна произвольной линейной поляризации, то она разлагается на две волны, имеющие ортогональные линейные поляризации и различные
VÔ1, VÔ 2 .
Это приводит:
1) К эффекту двойного лучепреломления, так как разные скорости соответствуют разным углам преломления (4.1).
2.К изменению вида поляризации. Действительно, если векторы напряженности полей с линейной поляризацией имеют вид
E1 x0 E0 cos(t k1z)
E2 y0 E0 cos(t k2 z),
то фазовый сдвиг между этим волнам
( (k1 k2 ) z) |
определяет вид поляри- |
||
зации. |
|
|
|
|
n , ëèí åéí àÿ |
||
|
|
(2n 1) |
|
(k1 k2 ) z |
, эллип тическая, |
||
|
|
|
|
|
|
||
Рисунок 4.1 |
|
2 |
|
с осями эллипса, совпадающими с осями координат.
43
4.3.3Электрооптические дефлекторы [8]
Дефлекторы – устройства отклонения луча – широко используются в современной электронной технике и, прежде всего, в голографических запоминающих устройствах (ГЗУ). Такие важные характеристики ГЗУ, как информационная емкость и быстродействие, в значительной степени определяются параметрами дефлектора. Дефлекторы бывают двух типов: акустооптические и электрооптические.
В акустооптическом дефлекторе акустооптическая частота должна изменяться дискретными ступенями, и выбор частот реализует специальный синтезатор частоты, управляемый обычно ЭВМ. В отличие от акустооптического дефлектора электрооптические дефлекторы (ЭОД) могут быть как дискретного, так и аналогового типа. Кроме того, она обладает более высоким быстродействием.
Примером электрооптического дефлектора аналогового типа является призменный дефлектор, в котором в качестве отклоняющего элемента применяется призма из электрооптического материала, помещенная в электрическое поле. При изменении величины электрического поля изменяется показатель преломления призмы и происходит отклонение преломленного светового луча.
Для практической реализации дефлектора этого типа требуются высокие управляющие напряжения 1ê для получения отклонения луча на угол порядка 1 мрад. Небольшой диапазон отклонения углов преломленного света обусловлен сравнительно малым изменением показателя преломления
n 10 3.
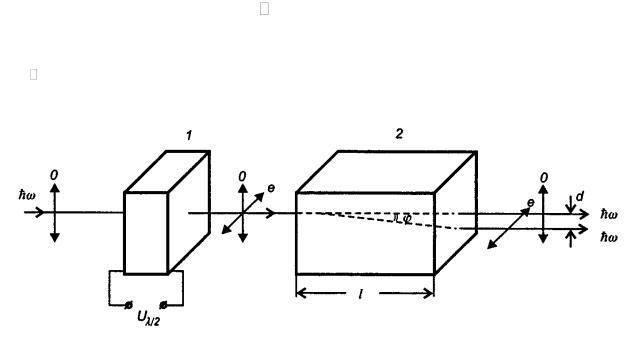
Рисунок 4.2. Ячейка цифрового электрооптического дефлектора:
о— обыкновеный луч, е — необыкновенный луч
Вголографических запоминающих устройствах обычно используют электрооптические дефлекторы дискретного типа, называемые цифровыми дефлекторами. Ячейка цифрового ЭОД изображена на рис. 4.2. Она состоит из электрооптического переключателя поляризации 1 и двупреломляющей пластин-

44
ки 2. В качестве переключателя поляризации используют ячейку Поккельса или Керра, а двупреломляющим элементом является кристалл исландского шпата CaCO3 . На вход переключателя поляризации 1 падает линейно поляри-
зованный луч. Переключатель позволяет изменять направление поляризации света в двух взаимоортогональных направлениях при подаче полуволнового напряжения U 2 . . Пластинка переключателя ориентирована таким образом,
что нормально падающий луч для нее является обыкновенным. На выходе луч может находиться в одном из двух состояний, соответствующих обыкновенному (U=0) или необыкновенному (U 2 .) лучу. Из двупреломляющей пла-
стинки 2 лучи выходят параллельно входному лучу, но один смещен относи-
тельно другого на расстояние d l tg , |
где tg |
n2 |
n2 |
|
0 |
e |
, |
||
|
|
|||
|
|
2n0ne |
||
n0 , ne — показатели преломления обыкновенного и необыкновенного
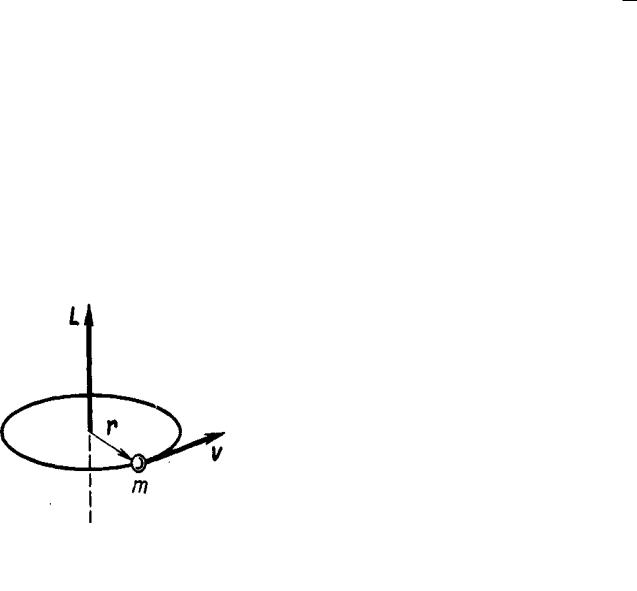
Рисунок 4.3. Схема электрооптического дефлектора из трех каска-
лучей, соответственно.
Рассмотренная ячейка представляет собой один каскад цифрового ЭОД. Если соединить последовательно N каскадов, каждый из которых дает
вдвое большее линейное смещение луча по сравнению с предыдущим каскадом, то такая система способна
адресовать световой луч в одну из 2N позиций на линии, как схематично изображено на рис. 4.3.
Двухкоординатный дефлектор состоит из двух последовательно расположенных блоков отклонения, каждый из которых отклоняет луч в направлении, перпендикулярном другому. При практической реализации ЭОД предъявляются высокие требования к точности конструкции и свойствам используемых материалов, поэтому чаще используются акустооптические дефлекторы, характеризующиеся большей простотой их изготовления.
45
4.4 Электромагнитные волны в гиротропных средах. Феррит в магнитном поле [2-6, 11, 12]
4.4.1Общие свойства феррита
Ферритами называют особую группу веществ, которые одновремено обладают магнитными свойствами ферромагнетиков и электрическим свойствами диэлектриков ( 5 20) . В отличие от ферромагнитных металлов
ферриты |
имеют |
весьма |
малую |
удельную |
проводимость |
( 10 4 |
10 6 ñèì / ì ) , |
и электромагнитные волны распространяются них с |
|||
небольшим затуханием. Совокупность целого ряда ценных свойств обуславливает широкое применение ферритов в радиотехнике.
В ненамагниченном состоянии феррит, как и любой другой ферромагнетик, представляет собой конгломерат большого числа областей, магнитные моменты которых ориентированны в различных направления. Под воздействием переменного электромагнитного поля магнитные моменты этих обла-
стей отклоняются от первоначального положения в направлении вектора H . В результате этого появляется суммарный магнитный момент единицы объема (т.е. вектор магнитной поляризации), совпадающий по направлению с вектором напряженности внешнего поля, поскольку магнитная восприимчивость и связанная с ней магнитная проницаемость являются скалярными величинами. Поэтому свойства ненамагниченного феррита для переменных полей любого направления оказываются одинаковыми, и распространение электромагнитных волн в нем происходит точно так же, как и в любой другой изотропной среде.
4.4.2 Физический механизм анизотропии ферритов. Уравнение движения намагниченности
Ферриты представляют собой твердые вещества, подобные керамике. Их получают искусственно, проводя высокотемпературное спекание оксида железа с соединением какого-либо двухвалентного металла, например Zn, Ba, Sr и т. д.
Условная химическая формула феррита имеет вид Mn (Fe2O3)n., где символом М обозначен ион двухвалентного металла.
При комнатной температуре электроны всех атомов, входящих в кристаллическую решетку феррита, прочно удерживаются обменными силами. Поэтому концентрация электронов в зоне проводимости весьма мала и ферриты в отличие от металлов проявляют четко выраженные свойства изолятора.
Классические представления, основан-
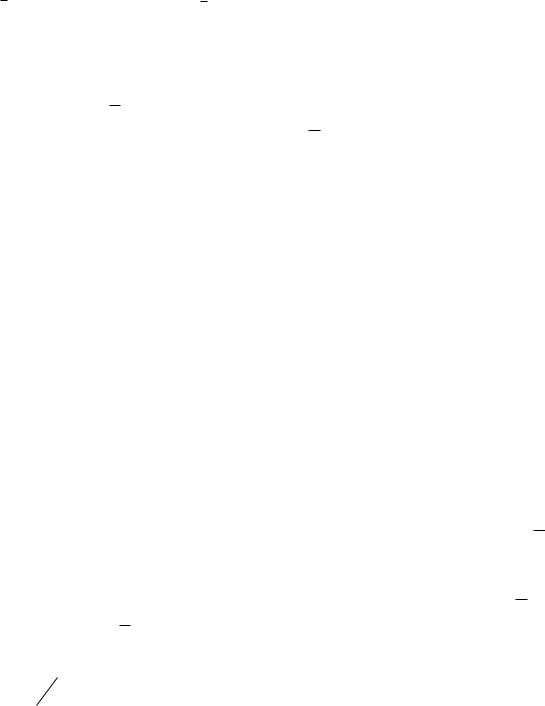
46
ные на понятии молекулярных токов, недостаточны для объяснения электромагнитных явлений в ферритах. Приходится использовать квантовомеханические понятия. Квантовая теория магнетизма веществ основана на том факте, что последний электрон в оболочке иона двухвалентного металла обладает магнитным и механическим моментами, или, как говорят в физике, такой электрон имеет спин.
Как известно, характеристикой тела, находящегося во вращательном движении, служит момент импульса.
Рассмотрим вращающуюся материальную точку массой т, имеющую
скорость v (рис. 4.4). Если через r обозначить радиус-вектор точки относительно центра вращения, то, по определению, момент импульса данной точки относительно центра вращения
|
|
|
|
|
) . |
|
L |
r |
(mv |
(4.24) |
|||
|
|
|
|
|
|
|
Ясно, что вектор L перпендикулярен плоскости орбиты точки.
Если на точку действует некоторая сила F , то справедлив закон Нью-
тона |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
). |
|
|
|
|
|||||
|
|
|
F |
|
(mv |
|
|
|
(4.25) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
||||
Векторно умножив левую и правую части равенства (4.25) на радиус- |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вектор r , получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|||||
|
|
rF |
r |
(mv |
) . |
( 4.26) |
|||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
dt |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Величину |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
K |
r |
F |
|
|
|
|
|
|
( 4.27) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
называют моментом силы относительно выбранной оси вращения. Воспользовавшись этим понятием, можно переписать уравнение (4.26) таким образом:
|
|
d |
|
|
|
( 4.28) |
|
K |
|
L |
|||||
dt |
|||||||
|
|
|
|
|
|
||
Пусть имеется некоторое материальное тело конечных размеров. Если это тело может силовым образом взаимодействовать с постоянным магнит-
ным полем, то говорят, что оно обладает некоторым магнитным моментом m Данный вектор имеет физическую размерность А/м2 и перпендикулярен плоскости воображаемого элементарного витка с током. В квантовой механи-
ке установлена числовая связь между магнитным моментом электрона m и
его моментом импульса L . Теоретически и экспериментально показано, что
|
|
|
|
|
|
|
|
|
|
m L, |
( 4.29) |
||
где e |
m |
1.76 10 11 |
Êë / êã |
- величина, равная отношению заряда |
||
|
|
|
|
|
|
|
электрона к его массе, и называется гиромагнитным отношением электрона.

47
Отрицательный знак в форме (4.29) указывает на то, что в пространстве век-
торы m è L антипараллельны.
Уравнение движения намагниченности. Предположим теперь, что обра-
зец феррита помещен в постоянное магнитное поле H 0 , ориентированное произвольным образом и называемое подмагничивающим полем. В курсе физики доказывается, что любая система, обладающая магнитным моментом,
стремится занять такое положение, чтобы векторы m è H 0 стали парал-
лельными. При таком положении потенциальная энергия магнитной системы оказывается минимальной.
Можно показать, что момент силы, действующей на систему в магнитном поле,
|
|
|
|
|
|
|
. |
|
K |
mH 0 |
( 4.30) |
||||||
0 |
|
|
|
|||||
Подставив это выражение в формулу (4.28) и учитывая соотношение (4.29), приходим к дифференциальному уравнению, которое описывает динамику вектора магнитного момента электрона:
|
|
|
|
|
|
|
|
|
|
|
d m |
|
|
|
|
|
. |
( 4.31) |
|||
mH 0 |
||||||||||
|
||||||||||
dt |
0 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|||
Предположим, что в единице объема феррита содержится N элементарных магнитных систем (валентных электронов). Тогда, введя вектор намагни-
ченности M mN из (4.31) получаем уравнение движения намагниченности.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d M |
|
|
|
|
|
|
|
0 |
. |
( 4.32) |
|||||||||||
|
M |
H |
||||||||||||||||||||
|
|
|
||||||||||||||||||||
|
dt |
|
|
|
|
|
0 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Частота ферромагнитного резонанса. Пусть для определенности посто- |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
янное подмагничивающее поле H 0 ориентировано вдоль оси z |
декартовой |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
системы координат, так что H 0 H0 iz . |
Вектор намагниченности является |
|||||||||||||||||||||
суммой составляющих по трем пространственным осям: |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
M M x ix M y i y M z iz . |
( 4.33) |
||||||||||||||||||||
Подставив это разложение в (3.31), получаем систему трех дифференциальных уравнений первого порядка
dM x 0 H0 M y , dt
dM y |
H |
M |
, |
( 4.34) |
|
|
|
||||
dt |
0 0 |
x |
|
|
|
|
|
|
|
||
dM z |
0, |
|
|
|
|
|
|
|
|
||
dt |
|
|
|
|
|
которая описывает свободное движение вектора намагниченности в феррите, происходящее без внешних возбуждающих сил.

48
Следует заметить, что в системе (4.34) третье уравнение, по сути дела, никак не связано с первыми двумя и просто означает, что. M z const. В тео-
рии ферритов часто приближенно считают, что продольная (вдоль поля H 0 ) проекция M z равна так называемой намагниченности насыщения Ms (от ан-
глийского, saturation — насыщение). Это означает, что все элементарные магнитные моменты ионов ориентированы вдоль направления подмагничивающего поля. Значения Ms оказываются различными у ферритов разных марок и приводятся в справочниках по радиотехническим материалам.
Обращаясь теперь к системе двух первых уравнений из (4.34), дополним ее некоторыми начальными условиями:
Mx |t 0 Mx0; M y |t 0 M y0 ,
где Mx0 è M y0 - произвольные постоянные величины, характеризу-
ющие состояние вещества при t=0. Совокупность уравнений (4.34) и начальных условий образует так называемую задачу Коши для рассматриваемых линейных дифференциальных уравнений. Подобные задачи встречаются в теории цепей, где они описывают процессы собственных колебаний.
Продифференцировав первое уравнение из (4.34) по времени воспользовавшись вторым уравнением, можно исключить неизвестную M y и полу-
чить уравнение второго порядка относительно проекции M x :
|
d 2M x |
2 M |
|
0. |
( 4.35) |
|
dt2 |
|
|||
|
ð |
x |
|
|
|
Входящий сюда параметр ð 0 H0 |
называют частотой ферро- |
||||
магнитного резонанса.
Уравнение (4.35) представляет собой хорошо известное уравнение гармонического осциллятора, которое в физике описывает свободные колебания в динамических системах второго порядка без потерь. Будем искать решение этого уравнения как сумму двух гармонических слагаемых с не известными пока амплитудными коэффициентами:
Mx (t) Acosðt Bsinðt. |
|
|
|
|
( 4.36) |
||||||
Прямая подстановка убеждает в том, что выражение (4.36) действи- |
|||||||||||
тельно служит решением уравнения (4.35). |
|
|
|
|
|
||||||
В соответствии с первым уравнением из системы (4.34) |
|
||||||||||
M |
|
|
1 |
|
dM x |
Asin |
t B cos |
t. |
( 4.37) |
||
y |
|
|
|||||||||
|
|
ð |
|
dt |
ð |
|
ð |
|
|
||
|
|
|
|
|
|
|
|
|
|||
Подставив значение t=0 |
в равенства (4.36) и (4.37), а также используя |
||||||||||
начальные условия (4.34), находим, что A Mx0 , B M y0 |
и поэтому |
|
|||||||||
M x |
M x0 cos ðt M y0 sin ðt, |
|
|
( 4.38) |
|||||||
M y |
M x0 sin ðt M y0 cos ðt. |
|
|
||||||||
|
|
|
|||||||||
49
Чтобы, уяснить физический смысл полученного результата, заметим,
что |
|
|
|
|
|
M 2 |
M 2 |
M 2 |
M 2 |
const, |
( 4.39) |
x |
y |
x0 |
y0 |
|
|
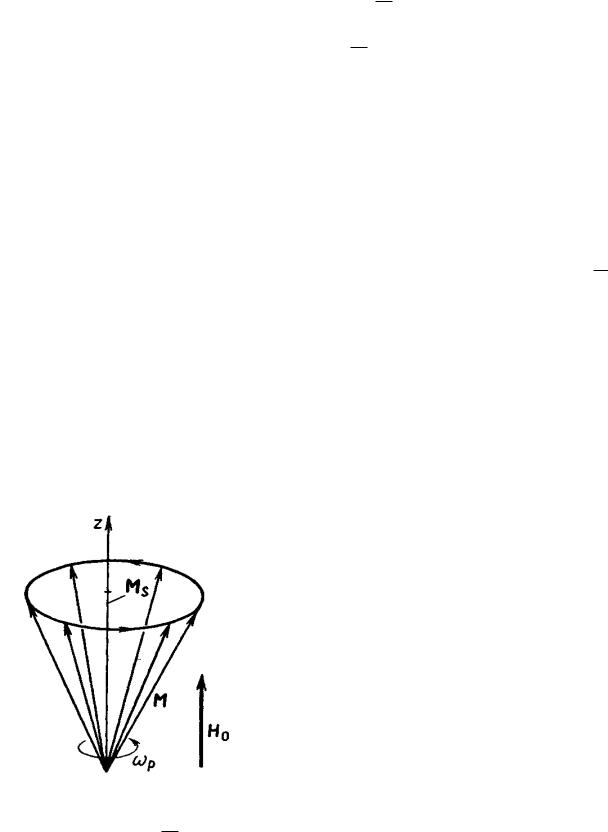
т. е. при свободных колебаниях вектор M перемещается в пространстве таким образом, что его конец описывает окружность постоянного радиуса
(рис. 4.4). Из рисунка видно, что вектор M всегда параллелен образующей конуса с высотой M S вращение вектора происходит с резонансной частотой,
а направление вращения зависит от начальных условий.
Движения такого вида часто встречаются в природе. Примерами могут служить круговое движение грузика, подвешенного на нерастяжимой нити, а также вращательное движение оси волчка, наблюдаемое в том случае, если внезапно возникает сила, действующая перпендикулярно оси вращения. В теории гироскопов такое движение волчка называют прецессией. По аналогии говорят, что рассмотренное явление в намагниченном феррите является свободной прецессией вектора намагниченности.
Частота ð зависит от напряженности подмагничивающего поля H 0 и
может оказаться весьма высокой. Например, если индукция подмагничивающего поля B0 1.5 Òë (такое поле можно создать с помощью мощного посто-
янного |
магнита) |
то |
|
ð |
H |
0 |
B 2 / 64 1011 |
c 1 |
|
|
|
|
0 |
0 |
|
||
или f ð 4.2 1010 |
Ãö 42 ÃÃö. Этой частоте соответствует длина волны λ0 = |
|||||||
7.14 мм, т.е. собственные колебания вектора намагниченности происходят в миллиметровом диапазоне.
Влияние затухания. Физически ясно, что амплитуда свободных колебаний вектора намагниченности с течением времени Должна уменьшаться из-за неизбежных потерь. Было предложено описывать потери в намагниченной среде, введя до-
полнительные члены в уравнения движения:
Рисунок 4.5. Свободное
движение вектора M
dM x |
|
|
M |
|
|
M x |
, |
|
||||
|
y |
|
|
|
||||||||
dt |
|
|
ð |
|
|
|
|
T |
|
|||
|
|
|
|
|
|
|
|
( 4.40) |
||||
dM y |
|
|
|
|
|
|
M y |
|
|
|||
|
M |
|
|
. |
|
|||||||
|
x |
|
|
|||||||||
dt |
ð |
|
|
|
|
T |
|
|||||
|
|
|
|
|
|
|
|
|||||
Уравнения вида (4.40) называют уравнениями Блока. Входящий в них параметр Т представляет собой время релаксации свободных колебаний вектора намагниченности. Значения Т находят экспериментально, изучая, например, отклик среды на внешнее воздействие вида короткого импульса или снимая амплитудно-частотную характеристику системы.
50
Покажем, что уравнения Блоха действительно описывают свободные колебания вектора намагниченности при наличии потерь. Для этого будем искать решения системы (4.40) в виде экспоненциальных функций времени с
не известными заранее коэффициентами:
M |
x |
Aept ; |
M |
y |
Bept . |
( 4.41) |
|
|
|
|
|
Подставив (4.41) в (4.40), убеждаемся, что коэффициенты А и В должны удовлетворять системе однородных линейных уравнений
|
1 |
|
|
p |
|
A |
ð B 0, |
|
|||
|
T |
|
|
ð A p 1 B 0.
T
Эта система будет совместной, если ее опре-
делитель равен нулю, т. е. параметр р является Рисунок 4.6. корнем квадратного уравнения
|
|
|
|
|
|
|
|
|
|
влияние потерь на M |
|
1 |
2 |
|
1 |
|
|
||
|
|
|
|
|
|||||
|
|
|
|
|
|
||||
|
|
p |
|
|
ð 0, откуда |
p1,2 |
|
j |
ð . |
|
|
|
T |
||||||
|
|
|
T |
|
|
|
|
||
( 4.42)
Подставляя эти значения корней в (4.40), приходим к выводу, что общий вид зависимостей поперечных проекций вектора намагниченности от времени таков:
M |
x, y |
e t T sin |
ð |
t. |
( 4.43) |
|
cos |
|
|
||
|
|
|
|
|
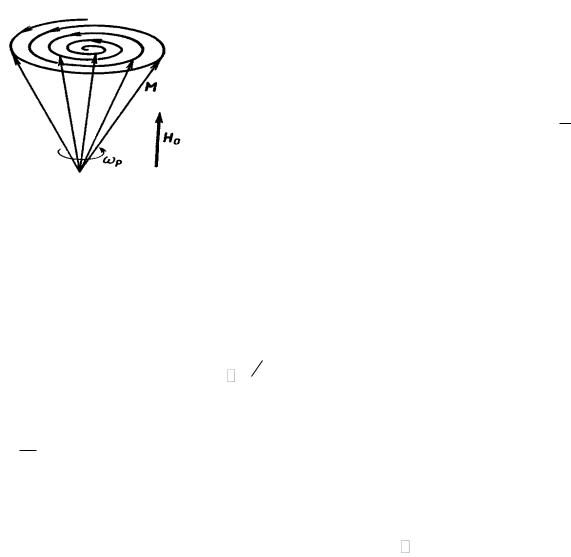
Эта формула очень напоминает ту, которая описывает свободный процесс в колебательном контуре без потерь. Легко сообразить, что конец векто-
ра M перемещается теперь не по окружности, как это было в случае среды без потерь, а по спирали (рис.4.6); при t этот вектор стремится стать параллельным подмагничивающему полю. Время релаксации Т служит оценкой длительности процесса установления равновесия в данной системе. Как правило, на практике выполняется неравенство ðT 1, т. е. прецессирующий
вектор намагниченности успевает совершить много оборотов вокруг оси, прежде чем процесс собственных колебаний закончится.
Недостаток уравнений Блоха состоит в том, что они введены чисто феноменологически, без обсуждения физического механизма возникновения потерь в феррите. Более последовательным оказывается подход, основанный на векторном уравнении движения намагниченности в форме Ландау - Лифшица
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
M |
M |
H |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
d M |
|
M |
|
H |
0 |
|
|
|
|
|
|
|
|
|
|
. |
( 4.44) |
||||
|
|
|
|
|
2 |
|
|
||||||||||||||
dt |
0 |
|
|
0 |
|
|
M |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Второе слагаемое правой части обычно называют диссипативным членом уравнения; параметр α определяют экспериментально.
