92
Резонансные |
потери. |
Потери, |
создаваемые |
упругими |
видами |
||||||
поляризации, |
пренебрежимо |
малы |
если |
поляризация |
происходит |
под |
|||||
действием переменных полей радиочастотного диапазона. Из-за малой |
|
||||||||||
амплитуды смещения частиц, они остаются в поле упругих сил. В условиях |
|
||||||||||
резонанса |
(инфракрасный |
диапазон |
частот) может |
резко |
измениться |
|
|||||
амплитуда и характер колебаний частиц, что приводит к нарушению условия |
|
||||||||||
упругости сил и возникновению потерь. Поэтому, резкому изменению |
|
||||||||||
диэлектрической |
проницаемости |
при |
|
резонансе |
частиц |
соответствует |
|||||
максимум тангенса диэлектрических потерь, что проиллюстрировано также |
|
||||||||||
на рисунке 3.14. |
|
|
|
|
|
|
|
|
|
||
Сегнетоэлектрические потери обусловлены движением границ доменов |
|
||||||||||
в диэлектриках, обладающих спонтанной поляризацией(такие диэлектрики |
|
||||||||||
называют сегнетоэлектриками). Эти потери существенны даже в условиях |
|
||||||||||
предельно |
низких |
частот |
и определяются чистотой и совершенством |
||||||||
внутренней структуры кристалла. О больших потерях в сегнетоэлектриках |
|
||||||||||
может свидетельствовать ярко выраженная петлеобразность характеристики |
|
||||||||||
D(E); для релаксационных видов поляризации она не столь значительна(см. |
|
||||||||||
выше). Более |
подробная |
информация |
о |
явлениях |
в |
сегнетоэлектриках |
|||||
изложена в пункте 3.11
3.11.4Тангенс угла диэлектрических потерь
Спрактической точки зрения материал можно считать диэлектриком,
если активная составляющая токаja |
значительно меньше реактивнойjр. |
|
Соотношение |
ja << jр , в свою очередь означает, что полный ток опережает |
|
напряженность |
электрического поля |
по фазе на угол, очень близкий кp/2 |
(рисунок 3.24). В данном случае опережение по фазе удобнее характеризовать не разностью фаз, а углом d, дополняющим сдвиг фаз до значения p/2.
Углом диэлектрических потерь d называется угол, дополняющий угол сдвига фаз между плотностью суммарного тока и напряженностью поля до значения p/2.
Чаще пользуются величиной не самого угла потерь, а его тангенсом, причем, как видно из рисунка (3.23),
tgd=ja/ip; |
(3.58) |
tgd=wa/wp. |
(3.59) |
Второе равенство получено формальным умножением числителя и знаменателя правой части первого равенства на действующее значение напряженности поля. Оно определяет tgd как отношение активной электрической мощности wа=jaE к модулю реактивной мощностиwp=jpE, усредненных по периоду.
93
Рассмотрим вопрос о зависимости тангенса угла потерь от частоты для модельного диэлектрика, имеющего сквозную проводимость и один тип релаксаторов со временем релаксацииt. Для рассматриваемого случая, необходимо амплитуду синусной составляющей плотности тока разделить на косинусную составляющую. На основе выражений (3.54) и (3.45) получим
g+ cp ×w 2t
|
e 0 ×w |
1 +w 2t 2 |
|
|
tgd = |
|
|
. |
(3.60) |
|
|
|||
|
|
cp |
|
|
1+ c y + 1 +w 2t 2
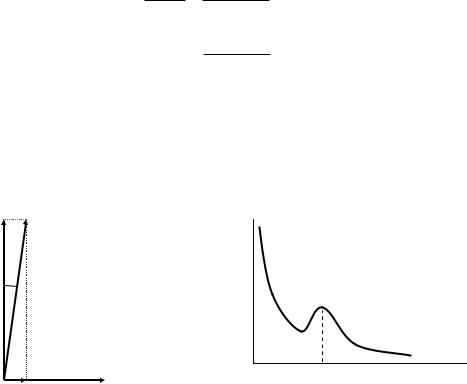
Эта зависимость качественно изображена на рисунке3.25 и имеет вид спадающей зависимости, на фоне которой проявляется релаксационный максимум (см. также рисунок 3.14). Положение максимума приблизительно соответствует условию w »1/t.
jр j d
jа E
Рисунок 3.24 - Векторная диаграмма составляющих тока и напряженности поля.
tgd
0 |
|
1/t |
w |
|
|
|
|
||
Рисунок 3.25 - Частотная зависимость |
|
|||
tgd |
диэлектрика |
с |
потерями |
|
проводимости |
и |
релаксационными |
||
потерями |
|
|
|
|
Тангенс угла диэлектрических потерь имеет важнейшее практическое значение и, например, связан с добротностью колебательных контуров, которых используются конденсаторы с диэлектрическими слоями. С другой стороны, эта величина, совместно с диэлектрической проницаемостьюe(w)
непосредственно измеряется некоторыми приборами. Поэтому, с учетом выражения wp=jрЕ=we(w)e0E2, следуемого из выражений (3.54) и (3.56), можно привести важнейшую и очевидную формулу, которой пользуются для
определения плотности мощности потерь в материале |
через известные |
||
значения e и tgd: |
|
||
|
|
. |
(3.61 ) |
|
wа = wee0E2 tgd |
||
94
Полезна также формула для полной мощности потерь в конденсаторе, имеющего емкость С с действующим напряжением на обкладкахU, которая, в свою очередь, следует из (3.61).
|
Wa= wCU2 tgd |
. |
(3.62) |
Необходимо, однако, помнить, что в ряде |
случаев формула(3.61) |
||
является более полезной, поскольку тепловая мощность в конденсаторе со сложной геометрией (в отличие от плоского конденсатора) может выделяться неравномерно из-за неоднородности поля. В этих случаях использование формулы (3.62) не дает объективной оценки режимов нагрева диэлектрика в отдельных областях.
3.11.5Схемы замещения конденсатора с потерями
Вряде случаев, особенно при анализе работы частотныхLC фильтров,
необходим |
учет |
диэлектрических |
потерь |
в |
конденсаторе. При |
этом |
|||||||||
конденсаторы с реальным диэлектриком, обладающим утечками и другими |
|||||||||||||||
потерями (см. подраздел 3.10) заменяют эквивалентной схемой. На рисунке |
|||||||||||||||
3.26, а |
изображена |
схема, имитирующая, конденсатор |
с |
|
диэлектриком, |
||||||||||
обладающим упругими и несколькими видами релаксационной поляризации с |
|||||||||||||||
|
|
|
|
|
|
6 |
В нее входит идеальный конденсатор, |
||||||||
различными временами релаксаций. |
|||||||||||||||
обладающий |
|
частью |
|
полной |
емкости, обусловленной |
геометрической |
|||||||||
емкостью и добавочной емкостью всех видов упругой поляризацииC0-у=C0 + |
|||||||||||||||
Cу=e0(1+cу)S/d. |
Потери |
проводимости |
имитируются |
параллельным |
|||||||||||
сопротивлением |
|
утечки RУТ=rd/S. |
Релаксационные |
|
виды |
поляризации |
|||||||||
создают дополнительные емкостиСр(i)=e0cр(i)S/d, |
"заряжающиеся |
|
через" |
||||||||||||
соответствующие |
"сопротивления |
потерь" Rр(i)=tр(i)d/(e0cр(i)S). |
|
Такая |
|
схема |
|||||||||
строго |
согласуется |
с |
теорией |
релаксационных потерь в диэлектриках. |
|||||||||||
Внешний элемент RВЫВ |
учитывает сопротивление выводов и сопротивление |
||||||||||||||
растеканию тока по обкладкам. В схеме опущены паразитные индуктивности |
|||||||||||||||
выводов и обкладок рулонной конструкции, которые, при необходимости |
|||||||||||||||
могут |
быть |
|
учтены. Преимуществом |
"развернутых" |
|
схем |
замещения, |
||||||||
подобных изображенной на рисунке3.26,а является то, что параметры всех элементов схемы не зависят от рабочей частоты. Недостатком является ее громоздкость. Использование таких схем все же не целесообразно, во-первых, потому, что все элементарные параметры каждой поляризацииtр(i) , cр(i) , как
6 При учете других видов неупругой поляризации (кроме релаксационных) эквивалентная схема будет сложнее. Упрощением является и то, что вклады всех видов упругой поляризации и геометрическая емкость имитируются общей емкостью С0-у. Это упрощение оправдано для радиочастот (см. пункт 4.9.1).
95
правило, являются неопределенными, даже при тщательных измерениях диэлектрического спектра. Во-вторых, для частотных фильтров, требующих максимальной стабильности параметровC и L, стараются выбирать конденсаторы с неполярными диэлектриками, обладающие минимальными утечками и релаксационными потерями. Потери оказывают непосредственное влияние на добротность колебательных контуров, снижая ее.
Учитывая сказанное, а также и ,точто доступными для измерения
параметрами является емкость и тангенс угла |
потерь конденсатора(для |
данной частоты), предпочтительными оказываются |
упрощенные схемы |
замещения, включающие в себя два элемента¾ идеальный конденсатор и резистор. Параметры каждой схемы определяются из условия соответствия отношения активной и реактивной мощностей измеряемому тангенсу угла
потерь. |
Для параллельной |
схемы |
замещения(см. |
рисунок |
3.26, |
б) |
||||||||
tgd = wa/wр = (т.к. UR=UC) = Ia/Ip = 1/(wCR), откуда следует |
|
|
|
|
||||||||||
|
|
|
|
|
|
RПР= 1/(wCtgd) . |
|
|
(3.63) |
|
||||
|
Для |
последовательной |
схемы |
замещения (см. |
рисунок |
3.26, |
в) |
|||||||
tgd = wa/wр = (т.к. IR=IC) = Ua/Up = R/(wC)), откуда следует |
|
|
|
|
||||||||||
|
|
|
|
|
|
RПС = tgd/(wC). |
|
|
(3.64) |
|
||||
|
|
|
|
RУТ |
|
|
|
RПР |
|
|
|
|
||
|
RВЫВ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
C0 |
|
|
|
C |
|
б) |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||||||
Rр1 |
Ср1 |
|
|
|
Rр2 |
Ср2 |
RПС |
С |
|
RрN |
а) |
в) |
||
СрN |
|
|
||
|
|
|
Рисунок 3.26 - Схемы замещения реального конденсатора.
Следует заметить, что в обеих схемах оба параметраR и C, вообще говоря, зависят от рабочей частоты. При этом значенияС(w) и tgd(w)
следует рассматривать как экспериментально измеряемые(например, резонансно-мостовыми методами), а значение R(w) ¾ как расчетное.