26
– ТАГ-системы и др.
При дальнейшем анализе мы будем пользоваться формализмом Тьюринга, вводя по мере надобности необходимые нам определения.
1.5.5 ПРОБЛЕМЫ
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Проблема – это утверждение (предикат), истинное или ложное в зависимости от входящих в него неизвестных (пере-
менных) определенного типа. Проблема обычно формулируется как вопрос.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · · · |
|
Пример · · · · · · · · · · · · · · · · · · · · · · · |
|
|
|
Например: «целое число x меньше целого y?».
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Частный случай проблемы – это набор допустимых значений ее неиз-
вестных. Отображение множества частных случаев проблемы во множество
{да, нет} называется решением проблемы. Если решение можно задать алго-
ритмом, то проблема называется разрешимой.
1.6 НЕКОТОРЫЕ ПОНЯТИЯ ТЕОРИИ ГРАФОВ
1.6.1 ОРИЕНТИРОВАННЫЕ ГРАФЫ
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Неупорядоченный ориентированный граф G – это пара
(A, R), где A – множество элементов, называемых вершинами, R
– отношения на множестве A. Пара (a, b) R называется дугой
(или ребром) графа G.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
|
27 |
|
· · · · · · · · · · · · · · · · · · · · · · · · |
|
Пример · · · · · · · · · · · · · · · · · · · · · · · |
|
||
|
|
|
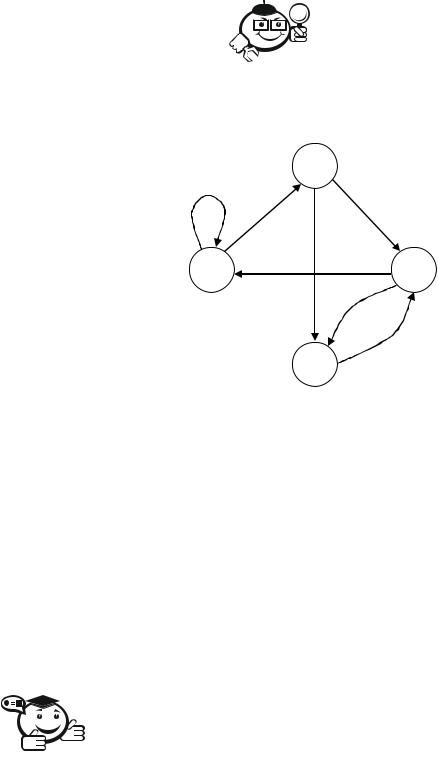
Граф G = (A, R), A = {1, 2, 3, 4}, R = {(1, 1), (1, 2), (2, 3), (2, 4), (3, 4), (4, 1), (4, 3)} (рис. 1.8).
2
1 |
4 |
3
Рисунок 1.8 – Пример ориентированного графа
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Пусть G1 = (A1, R1) и G2 = (A2, R2). Графы G1 и G2 являются равными (изоморфными), если существует биективное отображение f :A1→A2, такое,
что aR1b тогда и только тогда, когда f(a)R2f(b), т.е. в графе G1 из вершины a в
вершину b ведет дуга тогда и только тогда, когда в графе G2 из вершины, со-
ответствующей a, ведет дуга, соответствующая вершине b.
Части вершин и/или дуг графа иногда приписывают некоторую инфор-
мацию (разметку). Такие графы называются помеченными.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Пусть (A, R) – граф. Разметкой графа называется пара функций f и g, где f (разметка вершины) отображает A в неко-
торое множество, а g (разметка дуг) отображает R в некото-
рое (возможно, отличное от первого) множество.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
28
Графы G1 = (A1, R1) и G2 = (A2, R2) являются равными помеченными графами, если существует такое биективное отображение h: A1→A2, что:
1)aR1b тогда и только тогда, когда h(a)R2h(b), т.е. графы равны как не-
помеченные;
2)f1(a) = f2(h(a)), т.е. соответствующие вершины имеют одинаковые метки;
3)g1((a, b)) = g2((h(a), h(b))), т.е. соответствующие дуги имеют одина-
ковые метки.
· · · · · · · · · · · · · · · · · · · · · · · · |
|
|
|
Пример · · · · · · · · · · · · · · · · · · · · · · · |
||||
|
|
|
||||||
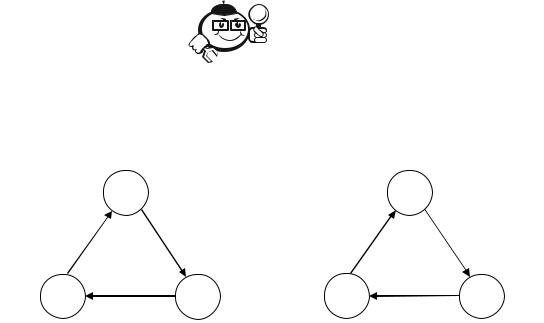
Рассмотрим графы G1 = {{a, b, c}, {(a, b), (b, c), (c, a)}} и G2 = {{0, 1, |
||||||||
2}, {(1, 0), (2, 1), (0, 2)}} (рис. 1.9). |
|
|
|
|
||||
|
x |
|
|
|
|
|
y |
|
|
b |
|
|
|
|
|
1 |
|
|
α |
α |
|
|
β |
α |
|
|
x |
a |
|
c |
y |
x |
0 |
2 |
x |
|
β |
|
|
|
|
|
α |
|
Рисунок 1.9 – Равные помеченные графы
Разметка графа G1 определяется формулами: f1(a) = f1(b) = x;
f1(c) = y;
g1((a, b))= g1((b, c)) = α; g1((c, a))= β.
Разметка графа G2 определяется формулами: f2(0) = f2(2) = x;
f2(1) = y;
g2((0, 2))= g2((2, 1)) = α;
29
g2((1, 0))= β.
Вывод: графы равны.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Последовательность вершин (а0, а1, …, аn), n 1 называется путем
длины n из вершины а0 в вершину аn, если для каждого 1 i n существует дуга, выходящая из аi–1 и входящая в вершину аi. Циклом называется путь (а0, а1, …, аn), в котором а0 = аn.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Граф называется сильно связанным, если для двух различ-
ных вершин a и b существует путь из a в b.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Степенью по входу вершины a назовем число входящих в нее дуг, степенью по выходу – число выходящих из нее дуг.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
1.6.2 ОРИЕНТИРОВАННЫЕ АЦИКЛИЧЕСКИЕ ГРАФЫ
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Ациклическим графом называется граф, не имеющий цик-
лов.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · · · |
|
Пример · · · · · · · · · · · · · · · · · · · · · · · |
|
|
|
Пример ациклического графа приведен на рис. 1.10.