121

Этот процесс называется нахождением транзитивного замыкания, а

сама матрица – матрицей достижимости. В этой матрице единицы соответ-

ствуют вершинам, между которыми есть соединительные пути.

На основании массива пустых строк матрицы можно проверить при-

знак LL(1). Там, где в левой части более одного правила появляется нетерминал, необходимо вычислить направляющие символы различных аль-

тернативных правых частей. Если для каких-либо из этих нетерминалов раз-

личные множества направляющих символов не являются непересекающими-

ся, грамматика окажется не LL(1). В противном случае она будет LL(1).

Рассмотренный выше алгоритм используется в двух целях:

1)для определения правильности (принадлежности) данной граммати-

ки к LL(1)-грамматике;

2)для преобразования произвольной грамматики к виду LL(1).

4.2.2 АЛГОРИТМ ПОИСКА НАПРАВЛЯЮЩИХ СИМВОЛОВ

Для построения таблицы разбора LL(1)-грамматики требуется опреде-

лить множество направляющих символов для всех правил грамматики. Кро-

ме того, эти множества также позволяют проверить, является ли грамматика корректной LL(1)-грамматикой.

· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·

Грамматику называют LL(1)-грамматикой, если для каж-

дого нетерминала, появляющегося в левой части более одного порождающего правила, множество направляющих символов,

соответствующих правым частям альтернативных порожда-

ющих правил, – непересекающиеся.

· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·

Для нахождения множества направляющих символов предварительно необходимо найти элементы двух вспомогательных множеств – множества предшествующих символов и множества последующих символов.

122

4.2.2.1 Множество предшествующих символов

Множество терминальных символов-предшественников (от англ. start)

определяется следующим образом:

a S(α) α * aβ,

где:

–a – терминал или пустая цепочка, а Σ{e};

–α и β – произвольные цепочки терминалов и/или нетерминалов, α,

β(N Σ)*;

–S(α) – множество символов-предшественников цепочки α.

То есть во множество символов-предшественников входят такие тер-

миналы, которые могут появиться в начале цепочки, выводимой из α. Пустая цепочка также может являться элементом множества S(α), если она выводит-

ся из α.

Дана грамматика:

P Ac

P Bd A a A Aa B b B bB

Здесь символы a и b – символы-предшественники для P.

· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·

Чтобы найти предшествующие символы, можно построить дерево вы-

вода для цепочки α. Причем, т.к. нас интересуют лишь терминалы, появляю-

щиеся в начале цепочек, следует:

123

1)использовать самые левые выводы (т.е. самый левый нетерминал цепочки заменять правыми частями соответствующих порождаю-

щих правил);

2)при появлении в дереве вывода цепочки, начинающейся с термина-

ла, терминал включать в искомое множество, а дальнейшее подде-

рево не строить, даже если в цепочке еще остались нетерминалы;

3)при появлении в дереве вывода пустой цепочки ее также включать в искомое множество.

Например, рассмотрим следующую грамматику:

A BCDF B 1 | 2 | e

C a | b | e

D x F y

Найдем множество символов-предшественников для α = A. Дерево вы-

вода, построенное по описанным выше правилам, приведено на рис. 4.1.

Стрелкой «↑» показаны позиции, в которых должны выводиться искомые терминалы. Жирным выделены найденные символы-предшественники.

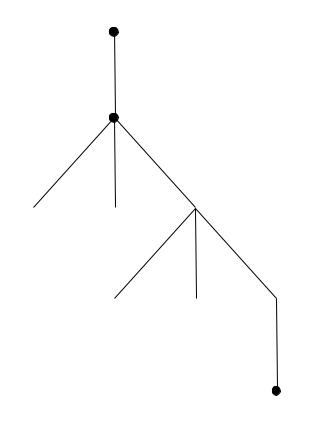
124

↑A

↑BCDF

↑CDF ↑1CDF ↑2CDF

↑DF ↑aDF ↑bDF

↑xF

Рисунок 4.1 – Дерево вывода для S(A)

Итак,

A 2 1CDF

A 2 2CDF A 3 aDF A 3 bDF A 4 xF

Следовательно, S(A) = {1, 2, a, b, x}. Аналогично можно строить мно-

жество предшествующих символов для любых других цепочек, составленных из элементов грамматики. Например:

S(BD) = {1, 2, x},

S(FDB) = {y},

S(BBF) = {1, 2, y},

S(BxB) = {1, 2, x},

125

S(BC) = {1, 2, a, b, e},

S(bAC) = {b}.

В этом несложно убедиться, построив деревья выводов для этих цепо-

чек.

· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·

Можно также сделать некоторые частные выводы:

–S(aβ) = {a}, где a Σ, а β – произвольная цепочка;

–S(e) = {e}.

Обобщая сказанное, получим формальное выражение для нахождения элементов множества предшествующих символов. Пусть α = X1X2…Xn, где

Xi N Σ{e}. Тогда:

S α k S Xi e ,

i 1

где:

e S X j e S X i ,i j , e S X i ,i 1, 2,..., n ,

e e S X ,i 1, 2,..., n ,

i

e S X e S X ,i j .

j i

То есть k – это номер первого символа цепочки, для которого e S(Xk).

Если же пустая цепочка присутствует во всех S(Xi), i = 1,2,…,n, то k = n. Пу-

стая цепочка войдет во множество S(α) только в том случае, если для любого

Xi, i = 1,2,…,n, выполняется условие e S(Xi). В этом случае получаем = {e},

в противном случае = .

Для нахождения множества символов-предшественников для левых ча-

стей всех правил грамматики G = (N, Σ, P, S) существует следующий нерекурсивный алгоритм:

126

1.Для всех правил грамматики (A α) P положить S(A) = .

2.Для каждого правила грамматики (A α) P добавить к множеству

S(A) элементы множества S(α), полученные по приведенной выше формуле:

То есть для терминала или пустой цепочки во множестве S(Xi) будет лишь один элемент – данный терминал или пустая цепочка. Для нетерминала множество S(Xi) получается путем объединения всех множеств символов-предшественников тех правил грамматики, у

которых данный нетерминал стоит слева от знака вывода.

3.Если при выполнении шага 2 хотя бы в одном множестве S(A) по-

явился хотя бы один новый элемент, вернуться на шаг 2. Иначе ал-

горитм заканчивает свою работу.

Рассмотрим работу этого алгоритма на следующем примере:

E T E′

E′ + T E′ | e T F T′

T′ * F T′ | e F ( E ) | a

или, что то же самое:

E T E′

127

E′ + T E′

E′ e

T F T′

T′ * F T′

T′ e

F ( E )

F a

Это уже рассмотренная ранее грамматика для математического выра-

жения, содержащего операции сложения и умножения, а также скобки и опе-

ранды a, преобразованная к виду LL(1). Имеем грамматику

G= (N, Σ, P, S) = ({E, E′, T, T′, F}, {+, *, (, ), a}, P, E).

Втабл. 4.7 приведены результаты последовательных проходов второго шага алгоритма.

Таблица 4.7 – Результаты проходов алгоритма поиска символов-предшественников

При четвертом проходе новые элементы во множествах S(A) не появят-

ся, поэтому он будет последним.

· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·