3.8 КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ МНОЖЕСТВА

83

Таким образом, утверждения:

1)L – регулярное множество;

2)L – праволинейный язык;

3)L – конечно-автоматный язык эквивалентны.

3.9МИНИМИЗАЦИЯ КОНЕЧНЫХ АВТОМАТОВ

3.9.1 ПОСТАНОВКА ЗАДАЧИ

Цель. Показать, что для каждого регулярного множества однозначно находится конечный автомат с минимальным числом состояний.

По данному конечному автомату M можно найти наименьший эквива-

лентный ему конечный автомат, исключив все недостижимые состояния и за-

тем склеив лишнее состояние. Лишнее состояние определяется с помощью разбиения множества всех состояний на классы эквивалентности так, что каждый класс содержит неразличимые состояния и выбирается как можно шире. Потом из каждого класса берется один представитель в качестве со-

стояния сокращенного (или приведенного) автомата [4].

Таким образом, можно сократить объем автомата M, если M содержит недостижимые состояния или два или более неразличимых состояний. Полу-

ченный автомат будет наименьший из конечных автоматов, распознающий регулярное множество, определяемое первоначальным автоматом M.

· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·

Пусть M = (Q, Σ, δ, q0, F) – конечный автомат, а q1 и q2 – два его различных состояния. Будем говорить, что цепочка x Σ*

различает состояния q1 и q2, если (q1, x) *(q3, e), (q2, x) *(q4, e) и

одно из состояний q3 и q4 принадлежит F. Будем говорить, что q1 и q2 k-неразличимы, и писать q1 k q2, если не существует такой цепочки x, различающей q1 и q2, у которой |x| ≤ k. Будем го-

84

ворить, что состояния q1 и q2 неразличимы, и писать q1 q2, ес-

ли они k-неразличимы для любого k ≥ 0.

· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·

Состояние q Q называется недостижимым, если не существует такой входной цепочки x, что (q0, x) *(q, e).

Автомат M называется приведенным, если в Q нет недостижимых со-

стояний и нет двух неразличимых состояний.

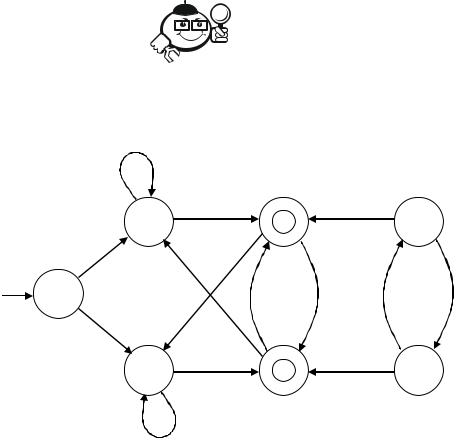
Рассмотрим конечный автомат M с диаграммой, изображенной на рис.

3.4.

Рисунок 3.4 – Диаграмма автомата

Чтобы сократить M, заметим сначала, что состояния F и G недостижи-

мы из начального состояния A, так что их можно устранить. Пока качествен-

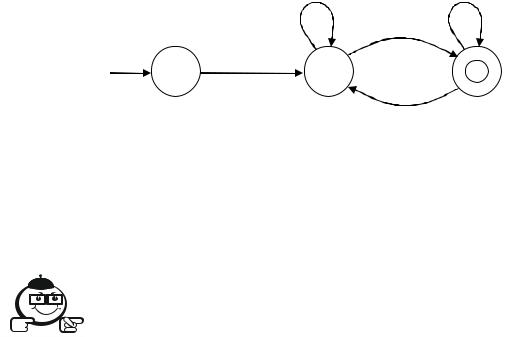
но, а позже строго мы установим, что классами эквивалентности отношений являются {A}, {B, D} и {C, E}. Тогда, взяв представителями этих множеств p, q и r, можно получить конечный автомат вида (рис. 3.5).

Рисунок 3.5 – Приведенный конечный автомат

· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·

Перед тем, как построить алгоритм канонического конечного автомата,

введем лемму.

· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·

Пусть M = (Q, Σ, δ, q0, F) – конечный автомат с n состояни-

ями. Состояния q1 и q2 неразличимы тогда и только тогда, когда они (n–2)-неразличимы, т.е. если два состояния можно различить,

то их можно различить с помощью входной цепочки, длина кото-

рой меньше числа состояний автомата.

·· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·

3.9.2АЛГОРИТМ ПОСТРОЕНИЯ КАНОНИЧЕСКОГО КОНЕЧНОГО АВТОМАТА

Вход. Конечный автомат M = (Q, Σ, δ, q0, F). Выход. Эквивалентный конечный автомат M'.

Метод.

Шаг 1. Применив к диаграмме автомата M алгоритм нахождения мно-

жества вершин, достижимых из данной вершины ориентированного графа,

найти состояния, достижимые из q0. Установить все недостижимые состоя-

ния.

Шаг 2. Строить отношения эквивалентности ≡0, ≡1 по схеме:

1)q1 ≡0 q2 тогда и только тогда, когда они оба принадлежат либо оба не принадлежат F;