Статистическая теория радиотехнических систем

3.3.2 Согласованный фильтр для прямоугольного радиоимпульса с ФКМ

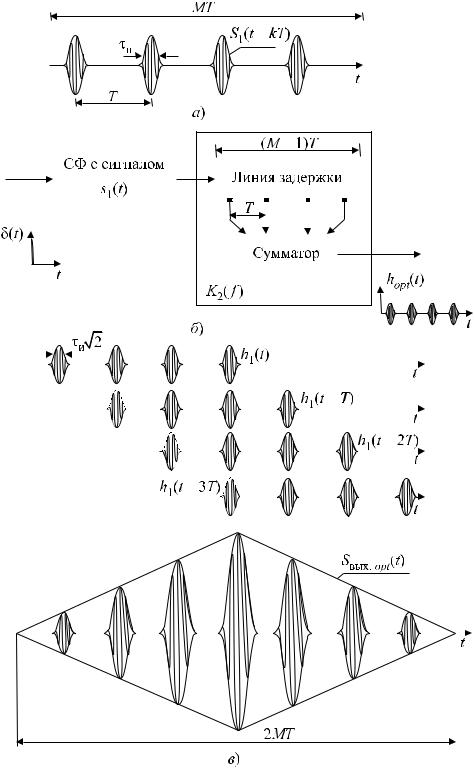
Рис. 3.3 – Обработка ФКМ радиоимпульса в согласованном фильтре:

а) модулирующая функция ФКМ сигнала; б) модулирующая функция импульсной реакции СФ; в) СФ для радиоимпульса с ФКМ

Определим структурную схему СФ для ФКМ импульса с семипозиционным кодом Баркера (рис. 1.15, a). На рисунке 3.3, a показано условное обозначение этого сигнала. Используя его и выражение (3.15), получаем импульсную реакцию СФ (рис. 3.3, б).

Устройство, оптимальной обработки ФКМ сигнала представлено на рисунке 3.3, в. Оно состоит из широкополосной линии задержки с семью равноотстоящими отводами (с интервалом задержки ), общего сумматора, к которому часть отводов подключена через инверсные каскады, а остальные — непосредственно, и линейного фильтра, согласованного с парциальным радиоимпульсом длительностью

= τи~7.

Работу СФ поясняет рисунок 3.4, на котором показаны этапы формирования радиоимпульса sвыx(t).

Рис. 3.4 – Формирование сигнала на выходе СФ: а) копии ФКМ импульса на выходах линии задержки; б) ФКМ сигнал на выходе сумматора;

в) огибающая ФКМ радиосигнала на выходе СФ

На рисунке 3.4, a схематически показаны (с учетом инверсных каскадов) радиоимпульсы с ФКМ на входе сумматора. Результат их суммирования представлен

на рисунке 3.4, б, а огибающая выходного сигнала СФ — на рисунке 3.4, в. Максимум сигнала sвыx(t) равен 7E1, где E1 — энергия парциального импульса.

3.3.3 Согласованный фильтр

для пачки M когерентных радиоимпульсов гауссовой формы

Представим входной сигнал, состоящий из M периодически следующих когерентных радиоимпульсов (рис. 3.5, a), в виде

коэффициенту передачи звена, обеспечивающего задержку сигнала на время mT. Суммирование слагаемых по формуле суммы конечного числа элементов геометри-

При подаче на вход СФ δ-импульса на выходе сумматора получается последовательность M (по числу отводов) радиоимпульсов, каждый из которых по форме повторяет импульсную реакцию фильтра, согласованного с одиночным импульсом пачки. На рисунке 3.5, в условно показан процесс оптимальной фильтрации пачки из M = 4 импульсов с симметричной огибающей гауссовой формы. Огибающая пачки радиоимпульсов на выходе сумматора Sвыx opt(t) имеет треугольную форму, длительность по нулям 2MT и число импульсов (2M −1).

Рассмотрим частотную интерпретацию работы СФ пачки. Определив из (3.27)

Рис. 3.5 – Пачка когерентных радиоимпульсов гауссовой формы (а), согласованный фильтр для пачки (б) и процесс фильтрации пачки (в)

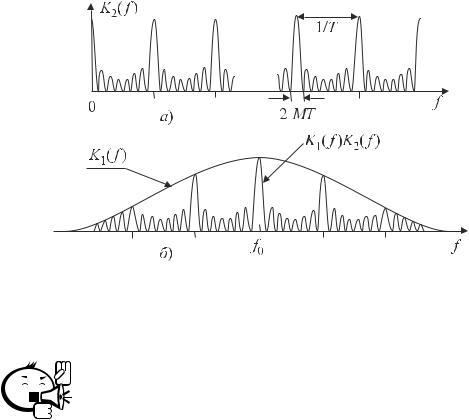
Частотная характеристика (3.28) является гребенчатой (рис. 3.6, a) с периодически повторяющимися через интервал 1~T зубцами, ширина которых по нулям 2~(MT). В случае идеальной линии задержки АЧХ (3.28) существует на всей оси частот. Результирующая АЧХ K(f ) = K1(f ) K2(f ) практически ограничена по

спектру колокольной (гауссовой) характеристикой K1(f ) фильтра, согласованного с одиночным импульсом пачки. Очевидно, что отношение с/ш по мощности в момент максимума сигнала на выходе СФ равно

что соответствует результатам п. 3.2. Напомним, что выигрыш в отношении с/ш получается за счет синфазного суммирования импульсных колебаний сигнала в определенный момент времени. Спектральные составляющие шума суммируются со случайными фазами.

Рис. 3.6 – Гребенчатая АЧХ схемы оптимального суммирования (а) и результирующая АЧХ (б) согласованного фильтра

для когерентной пачки радиоимпульсов

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Гребенчатая структура АЧХ СФ, совпадающая со структурой амплитудно-частотного спектра когерентной пачки импульсов, обеспечивает прохождение через СФ только части спектральных составляющих помехи.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Наименьшее усиление СФ имеет на тех участках спектра, где уровень сигнальных составляющих мал.

3.4 Обнаружение и различение сигналов при наличии помех

Статистическая теория принятия решений при наличии помех включает два основных раздела: первый — статистическая теория проверки гипотез и второй — статистическая теория оценок неизвестных параметров. Для решения задач оптимального обнаружения, различения и классификации сигналов обычно приме-

няют аппарат теории проверки гипотез. Рассмотрим две наиболее простые задачи: различения и обнаружения сигналов в бинарном случае.

Задача различения двух сигналов (байесов метод)

Постановка задачи. Наблюдаемый сигнал на входе приемника представим

где θ— случайная величина с двумя значениями 0 и 1. Априорные вероятности значений известны: P(θ = 0) = p0 и P(θ = 1) = p1. Статистические свойства помехи и сигналов предполагаются также заданными. Таким образом, при дискретном отборе данных на интервале [0, T] могут быть определены n-мерные условные ПРВ (см. п. 1.4):

где H0 и H1 — две случайные гипотезы (события), соответствующие двум возможным состояниям наблюдаемого сигнала: θ = 0 и θ = 1. Оптимальный различитель на основе обработки сигнала y(t) должен лучшим способом принять решение о том, какая из двух гипотез реализовалась в конкретном наблюдении. Фактиче-

ские данные наблюдений в статистике называют выборкой; в нашем случае это n-мерный вектор y = {y1, y2, . . ., yn}, где yi = y(ti), i = 1, . . ., n.

Данная задача относится к статистической теории проверки гипотез. Рассмотрим далее байесов метод ее решения.

Решение задачи. Очевидно система различения может из-за влияния помех

а 2 и 4 — ошибочному.

Для определения количественного критерия эффективности различения назначим «плату» за результат работы системы, которая зависит от состояния на входе и выходе и определяется риском, который несет «лицо», использующее результаты различения сигналов. Введем платежную матрицу C = {Cij}, где i, j = 0, 1; первый индекс определят принятую гипотезу на выходе (решение), второй — гипотезу на входе. Без потери общности рассуждений будем полагать плату за ошибки положительной, т. е. C10, C01 > 0 и за верные решения C00, C11 0. Элементы Cij записаны в таблице 3.1.

Таблица 3.1 – Элементы Ci j

Критерий оптимальности различителя. В качестве критерия используем величину средней «платы», т. е. ее математическое ожидание потерь. В теории принятия решений эту величину называют средним риском R. По правилу вычисления среднего дискретной случайной величины C получим:

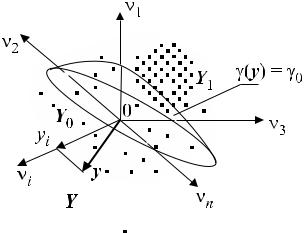
Для наглядности дальнейших рассуждений используем геометрическую интерпретацию задачи. На рисунке 3.7 условно показано n-мерное евклидово пространство с осями координат 0νi(i = 1÷n). Множество возможных выборочных значений y обозначим Y (иногда его называют пространством наблюдений). Любому выборочному вектору у Y соответствует точка с координатами (y1, y2, . . ., yi, . . ., yn). Одна из них yi показана на рисунке.

Рис. 3.7 – Пространство наблюдений

Очевидно, что решающее правило в бинарном случае сводится к тому, чтобы найти способ разбиения множества Y на сумму двух непересекающихся подмножеств Y 0 и Y1, т. е. Y = Y0 Y1. И далее, если y Y 0, то принимается решение H0; про-

Â

если y Y1, то принимается решение H1. Конкретное разбиение в n-мерном

говое значение — величину γ0. Заметим, что любое преобразование наблюдаемых данных в статистических задачах называют статистикой.

Важно отметить, что статистика γopt(y) осуществляет редукцию исходных данных: на входе «наблюдатель» располагает n-мерным вектором y, который содержит информацию о переданном сигнале; на выходе после обработки получена скалярная величина γ. Очевидно, что при таком взаимно неоднозначном преобразовании первичная информация, в общем случае, может быть частично утрачена.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Удивительно, однако, то, что существуют такие статистики (их называют достаточными), которые, несмотря на редукцию первичных данных, не ведут к потере полезной информации, содержащейся в них. Интуитивно понятно, что оптимальное решающее правило должно бы обладать этим замечательным свойством.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Оптимальное решающее правило найдем из условия минимума среднего риска (МСР) (3.32). Запишем выражения для условных вероятностей в виде интегралов от соответствующих n-мерных условных ПРВ по области Y0:

Подставив выражения (3.33) в формулу (3.32), после группирования слагаемых с учетом того, что P(H0) = p0 и P(H1) = p1, получим:

Первые два слагаемых постоянны и от выборки y не зависят. Подынтегральное выражение при любых y есть разность положительных величин, поскольку C01 >

Структура устройства, которое реализует оптимальный алгоритм различения сигналов, определяется конкретным видом условных ПРВ.

3.5 Другие критерии оптимальности обнаружения и различения

Можно предположить, что в зависимости от критерия оптимальности может измениться правило принятия решения, т. е. способ обработки входного сигнала. Во всяком случае, повседневный опыт это подтверждает. Например, от критерия оценки работы сотрудника зависит стратегия его поведения. Покажем, что байесов критерий (МСР) является вполне общим, т. е. к нему сводятся другие не менее целесообразные критерии. Предварительно представим (3.32) для величины R в виде

Критерий минимума взвешенной вероятности ошибки. Выше отмечалось, что в бинарной задаче проверки гипотез возможны 4 исхода, из которых два оши-

где k1 и k2 — весовые коэффициенты, зависящие от потерь, которые возникают вследствие допущенных ошибок. Сравнивая (3.38) и (3.39), видим, что величи-

на Koш = R, если C11 = C00 = 0 и k1 = p0C10, k2 = p1C01. Следовательно, данный критерий есть частный случай критерия МСР.

2. Критерий идеального наблюдателя. Критерий состоит в том, что в системе принятия решений необходимо обеспечить минимум полной вероятности ошибоч-

терий, когда k + k = 1 и обе ошибки одинаково опасны. Подобная ситуация ха-

1 2 ( ) ( )

рактерна для различения сигналов в цифровых системах связи, где s0 t и s1 t используются для передачи 0 и 1. Таким образом, этот критерий также следует из критерия МСР.

3. Критерий Неймана — Пирсона. Для РЛ систем характерна ситуация, когда

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Оптимальный РЛ приемник обнаруженияÂдолжен обеспечить максимальную величину P‰H1~H1Ž = 1 − P‰H0~H1Ž = D (detection) —

вероятности правильного обнаружения при заданной величине F. Это условие носит название критерия Неймана — Пирсона. Данный критерий также следует из критерия МСР как частный случай [1].

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . Выводы . . . . . . . . . . . . . . . . . . . . . . . . .

Таким образом, для всех перечисленных выше критериев способ обработки остается неизменным, т. е. оптимальный различитель (обнаружитель) формирует величину L(y) — отношение правдоподобия. Отличие устройств обработки состоит в выборе стоимостей за принятые решения, которые влияют только на порог γ0.

.. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3.6Различение двух детерминированных сигналов на фоне белого гауссова шума. Структура оптимальных устройств

Наблюдаемый сигнал на входе приемника представим в виде (3.30), полагая сигналы s0(t, λ0) и s1(t, λ1) точно известными:

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Важное условие, при котором мы решаем задачу, состоит в том, что предполагаются точно известными моменты начала и окончания временного интервала, в котором находится полезный сигнал s(t). Неизвестно лишь то, какой это сигнал: s0(t) или s1(t).

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Гауссов белый стационарный шум n(t) имеет нулевое среднее значение и корреляционную функцию Kn(τ) = ‰N0~2Žδ(τ) (см. (1.48)).

Определим в явном виде отношение правдоподобия (3.37) для дискретной вы-

борки из наблюдаемого сигнала (3.41). Для двух гипотез на входе приемника имеем:

том (1.44) m-мерные условные ПРВ выборочного вектора y для двух гипотез имеют вид:

где m = T~ t — число отсчетов на интервале наблюдения. Подставляя (3.43) в (3.37), после выполнения простых алгебраических преобразований получим:

Выражение (3.44) определяет искомое отношение правдоподобия для задачи различения двух сигналов с полностью известными параметрами на фоне помехи в виде квазибелого шума. Оно допускает простой предельный переход к случаю белого шума, когда fв → ∞, a t → 0. При этом суммы в показателе степени первого сомножителя перейдут в интегралы, численно равные энергии различаемых сигналов:

Сумма в показателе второго сомножителя перейдет в интеграл: