Раздел 13. Выборка и способы ее представления. Выборочные параметры распределения

Математическая статистика – это наука о математических методах, позволяющих получать обоснованные выводы о параметрах, видах распределений и других свойствах случайных величин по конечной совокупности наблюдений над ними – выборке.

Выборка понимается следующим образом. Пусть случайная величина X наблюдается в случайном эксперименте В. Повторим эксперимент В n раз, предполагая, что условия проведения эксперимента, а следовательно, и распределение наблюдаемой случайной величины X не изменяются от эксперимента к эксперименту. Этот новый составной эксперимент связан с n - мерной случайной величиной – случайным вектором X1, X2 ,..., Xn , где X j

– случайная величина, соответствующая j -му эксперименту. Очевидно, X j , j 1,2,..., n , – независимые в совокупности случайные величины, каждая

из которых имеет тот же закон распределения, что и случайная величина X . Закон распределения случайной величины X называется распределени-

ем генеральной совокупности, а случайный вектор X1, X2 ,..., Xn – выбо-

рочным вектором. Числа x1,..., xn , получаемые на практике при n - кратном повторении эксперимента в неизменных условиях, представляют собой реализацию выборочного вектора и называются выборкой x1,..., xn объема n .

Выборку x1, x2 ,..., xn при необходимости можно рассматривать как точку выборочного пространства, т.е. множества, на котором задано распределение выборочного вектора X1, X2 ,..., Xn . Аналогично определяется выборка в случае, когда случайный эксперимент связан с несколькими случайными величинами. Например, выборка объема n из двумерной генеральной совокупности есть последовательность x1, y1 ,..., xn , yn пар значений случайных величин X и Y , принимаемых ими в n независимых повторениях случайного эксперимента.

100

Способы представления выборки

Результаты наблюдений x1, x2 ,..., xn генеральной совокупности X , записанные в порядке их регистрации, обычно труднообозримы и неудобны для дальнейшего анализа. Задачей статистического описания выборки является получение такого ее представления, которое позволяет выявить характерные особенности совокупности исходных данных.

Вариационным рядом выборки x1, x2 ,..., xn называется способ ее записи, при котором элементы упорядочиваются по величине, т.е. записываются в виде последовательности x 1 , x 2 ,..., x n , где x 1 x 2 ... x n . Разность

между максимальным и минимальным элементами выборки x n x 1

называется размахом выборки.

i 1

называется последовательность пар zi , ni . Обычно статистический ряд за-

писывается в виде таблицы, первая строка которой содержит элементы zi , а вторая – их частоты.

При большом объеме выборки ее элементы объединяют в группы (разряды), представляя результаты опытов в виде группированного статистического ряда. Для этого интервал, содержащий все элементы выборки, разбивается на k непересекающихся интервалов. Вычисления значительно упроща-

ются, если эти интервалы имеют одинаковую длину b k . В дальнейшем

подразумевается именно этот случай. После того как частичные интервалы выбраны, определяют частоты – количество ni элементов выборки, попавших в i -й интервал (элемент, совпадающий с верхней границей интервала, относится к последующему интервалу). Получающийся статистический ряд в верхней строке содержит середины zi интервалов группировки, а в нижней – частоты ni – i 1,2,...,k .

101

Наряду с частотами одновременно подсчитываются также накопленные

i

частоты n j , относительные частоты ni n и накопленные относительные

j 1

называемую таблицей частот группированной выборки.

Следует помнить, что группировка выборки вносит погрешность в дальнейшие вычисления, которая растет с уменьшением числа интервалов.

Пусть x1, x2 ,..., xn – выборка из генеральной совокупности с функцией распределения FX x . Распределением выборки называется распределение дискретной случайной величины, принимающей значения x1, x2 ,..., xn с вероятностями 1/ n . Соответствующая функция распределения называется эмпи-

где суммируются частоты тех элементов выборки, для которых выполняется

кусочно-постоянную функцию.

Аналогично определяется эмпирическая функция распределения для группированной выборки. При каждом x Fn x сходится по вероятности к

FX x и, следовательно, при большом объеме выборки может служить при-

ближенным значением (оценкой) функции распределения генеральной сово-

купности в каждой точке x .

В ряде случаев для наглядного представления выборки используют ги-

стограмму и полигон частот.

Гистограммой частот группированной выборки называется кусочнопостоянная функция, неизменная на интервалах группировки и принимаю-

102

щая на каждом из них значения nbi , i 1,2,..., k ,. Площадь ступенчатой фигу-

ры под графиком гистограммы равна объему выборки n .

Аналогично определяется гистограмма относительных частот. Пло-

щадь соответствующей ступенчатой фигуры для нее равна единице. При увеличении объема выборки и уменьшении интервала группировки гистограмма относительных частот является статистическим аналогом плотности распределения WX x генеральной совокупности.

Полигоном частот называется ломаная с вершинами в точках zi , ni , i 1,2,..., k , а полигоном относительных частот – ломаная с вершинами в

получается из полигона частот сжатием по оси Oy в n раз.

Если плотность распределения генеральной совокупности является достаточно гладкой функцией, то полигон относительных частот является более хорошим приближением плотности, чем гистограмма.

Выборочные параметры распределения

Пусть x1, x2 ,..., xn – выборка объема n из генеральной совокупности с функцией распределения FX x . Рассмотрим выборочное распределение, т.е.

распределение дискретной случайной величины, принимающей значения x1, x2 ,..., xn с вероятностями, равными 1/ n . Числовые характеристики этого выборочного распределения называются выборочными (эмпирическими) числовыми характеристиками. Следует отметить, что выборочные числовые характеристики являются характеристиками данной выборки, но не являются характеристиками распределения генеральной совокупности. Чтобы подчеркнуть это различие, выборочные характеристики в дальнейшем будем обозначать теми же символами, что и ранее, но со значком * наверху. Некоторые выборочные характеристики имеют традиционные обозначения, например, x – выборочное среднее.

Математическое ожидание дискретной случайной величины определяет-

n

ся по формуле mX p j x j .

j 1

103

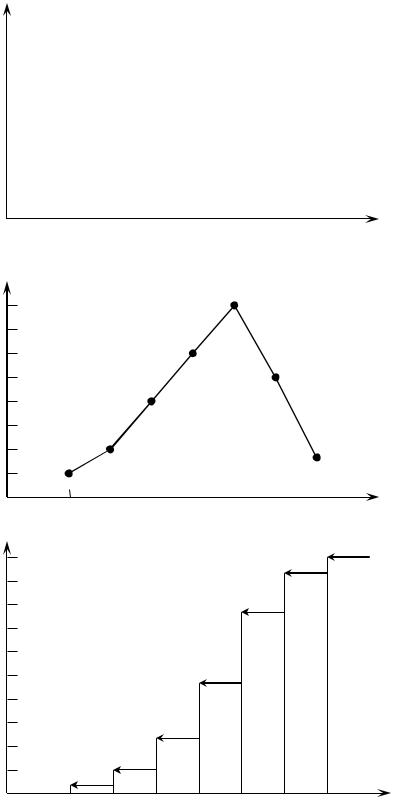
ным третьего и последнего столбцов таблицы. Fn x имеет скачки в точках,

соответствующих серединам интервалов группировки. В результате получа-

ni

16

12

8

4

Fn x

1,0

0,8

0,6

0,4

0,2

Рис. 13.3.

106

Пример 4

Определить выборочное среднее и выборочную дисперсию для выборки

5, 6, 8, 2, 3, 1, 1, 4.

Решение. Представим данные в виде вариационного ряда: 1, 1, 2, 3, 4, 5,

6, 8.

Выборочное среднее m*X 18 1 1 2 3 4 5 6 8 3,75 . Выборочная дисперсия

D*X 18 12 12 22 32 42 52 62 82 3,752 5,44.

Задачи

Для каждой из приведенных ниже выборок определить размах, а также построить вариационный и статистический ряды.

13.1.11, 15, 12, 0, 16, 19, 6, 11, 12, 13, 16, 8, 9, 14, 5, 11, 3.

13.2.17, 18, 16, 16, 17, 18, 19, 17, 15, 17, 19, 18, 16, 16, 18, 18.

13.3. В группе на занятии по статистике проводится эксперимент по регистрации номера месяца рождения каждого из студентов группы. Построить вариационный и статистический ряды полученной выборки.

В задачах 13.4, 13.5 найти размах выборки, число и длину интервалов, а также составить таблицу частот (границы первого интервала указываются).

13.4. Время решения контрольной задачи студентами (в секундах):

Первый интервал: 14–23.

13.5. Продолжительность работы батареек одного типа (в часах):

Первый интервал: 8,4–10,4.

107

В задачах 13.6–13.9 построить графики эмпирических функций распределения, гистограммы и полигоны частот для выборок, представленных статистическими рядами.

13.6.

Построить гистограмму и полигон относительных частот по этой выборке, предварительно проведя группировку. В качестве длины интервала взять следующие значения: а) b 0,3 ; б) b 0,6 ; в) b 1,2 .

108

Вычислить среднее и дисперсию следующих выборок:

13.11. 7, 3, 3, 6, 4, 5, 1, 2, 1, 3.

13.123,1; 3,0; 1,5; 1,8; 2,5; 3,1; 2,4; 2,8; 1,3.

13.13а) 1, 2, 3, 4, 5, 5, 9; б) 1, 2, 3, 4, 5, 5, 12. Сравнить полученные числовые результаты для выборок а) и б).

В задачах 13.14.–13.16. определить среднее и дисперсию группированных выборок.

13.17. Предположим, что в результатах наблюдений случайной величины X присутствует одна и та же систематическая погрешность a . Какое влияние оказывает эта систематическая погрешность на величины выборочных среднего и дисперсии?

109