
Анализ временных характеристик аналоговых устройств
..pdf
71
уравнения относительно выходного напряжения, исследуемой активной RC - цепи второго порядка с последовательной ООС
v''(t) ( 1 |
2) v'(t) |
1 2 v(t) K0 [ '(0) b (0)] . |
Данное уравнение является неоднородным обыкновенным дифференциальным уравнением второго порядка. В нормальной форме Коши, уравнение, разрешенное относительно старшей производной, имеет вид
v''(t) |
( 1 |
2 ) v'(t) |
1 2 v(t) K0 [ '(0) b (0)]. |
Прежде, чем приступить к интегрированию полученного неоднородного обыкновенного дифференциального уравнения, с целью получения частного решения, необходимо определить начальные условия v(0) и v'(0) .
Определение начальных условий. Для определения начальных условий удобно воспользоваться теоремой операционного исчисления о начальном значении функции оригинала
v(0) |
lim |
v(t) |
lim |
p V ( p) |
lim |
|
|
K0 |
p ( p b) |
K0 |
; |
|
||||||
|
( p |
1) ( p |
2) |
|
|
|||||||||||||
|
t |
0 |
|
|
p |
|
|
|
p |
|
|
|
|
|
||||
' |
|
|
' |
|
|
|
2 |
|
|
|
|
K0 |
p2 ( p b) |
|
|
|
||
v |
(0) |
lim |
v |
(t) |
lim |
p |
|
V ( p) |
lim |
|
|
|
|
|
. |
|
||
|
( p |
1) ( p |
2 ) |
|
|
|||||||||||||
|
t |
0 |
|
|
p |
|
|
|
p |
|
|
|
|
|
||||
Заметим, что первое начальное значение, совпало с ранее найденным |
||||||||||||||||||
значением импульсной характеристики, при t |
|
|
0 . |
|
|
|
|
|
|
|||||||||
В последнем дробно-рациональном выражении степень числителя |
||||||||||||||||||
превысила степень |
знаменателя, |
и взятие |
предела дает |
значение |
, не |
|||||||||||||
раскрывая ее составляющие. Раскрыть конечные и бесконечные составляющие этого предела можно путем последовательного деления числителя на знаменатель, до тех пор, пока степень остатка не станет равной степени знаменателя. При этом, целые части от деления дают составляющие
(0), |
'(0), |
''(0), |
и так далее, |
а остаток деления в пределе при |
p |
|||||||||||
дает конечную часть начального условия. |
|
|
|
|
|
|||||||||||
|
Следуя указанной модификации теоремы о начальном значении, |
|||||||||||||||
получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
' |
|
|
' |
|
|
|
2 |
|
|
|
K0 p2 ( p b) |
|
||||
v |
(0) |
lim |
v |
(t) |
|
lim p |
|
V ( p) |
lim |
|
|
|
|
|
|
|
|
|
( p |
|
1) ( p |
2 ) |
|
|
|||||||||
|
|
t 0 |
|
|
|
p |
|
|
p |
|
|
|
|
|||
|
lim |
K0 |
p |
[b ( 1 |
|
2 )] p2 |
|
1 2 |
p |
K0 |
(0) [b ( 1 |
2 )] . |
||||
|
|
( p |
|
1) ( p |
|
2 ) |
|
|
||||||||
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таким образом, полученное выражение совпало с начальным значением производной импульсной характеристики, полученной на основании теоремы о дифференцировании оригинала.

72
Приступаем к интегрированию дифференциального уравнения с целью определения отклика, исследуемой активной RC - цепи второго порядка с последовательной ООС, на единичный скачок на входе.
Метод Лагранжа или метод вариации произвольных постоянных.
Согласно методу Лагранжа, общее решение неоднородного дифференциального уравнения, записывается аналогично решению однородного уравнения, только константы при фундаментальных решениях заменяются неизвестными функциями времени
|
v(t) C (t) f (t) C (t) f |
2 |
(t) C (t) e |
1 t C (t) e |
2 t , |
|||
|
|
1 |
1 |
2 |
1 |
2 |
|
|
где |
C1(t), C2 (t) - |
неизвестные |
функции - |
варьируемые |
постоянные; |
|||
f1(t), |
f2 (t) - |
фундаментальная |
|
система |
решений |
однородного |
||
дифференциального уравнения второго порядка.
Варьируемые или произвольные постоянные C1(t), C2 (t) находятся из
определяющей системы уравнений Лагранжа, представляющей собой условия, ограничивающее появление производных от неизвестных функций, выше первого порядка, при дифференцировании решения общего вида и результат подстановки общего решения в исходное уравнение
C' |
(t) |
f (t) C' |
(t) f |
2 |
(t) 0 |
|
|
1 |
|
1 |
2 |
|
|
, |
|
C' |
|
f '(t) C' |
(t) f ' |
|
|||
(t) |
(t) F (t) |
|
|||||
1 |
|
1 |
2 |
|
2 |
|
|
где F(t) - правая часть дифференциального уравнения.
Таким образом, определяющая система Лагранжа имеет вид
|
|
|
' |
|
|
|
|
1 t |
' |
(t) e |
2 t |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
C1(t) e |
|
|
C2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|||||||||
|
|
|
' |
|
|
|
|
|
|
1 t |
|
' |
|
|
|
|
|
|
|
2 t |
|
|
|
|
' |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
1 |
e |
|
(t) |
|
2 e |
K0 |
|
[ |
(0) |
b |
|
(0)] |
|
|
|||||||||||||
|
|
C1(t) |
|
C2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Определим |
C' (t) |
и |
C |
' |
(t) |
|
|
из предыдущей |
системы |
уравнений, |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
воспользовавшись правилом Крамера |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
e |
1 t |
|
|
e |
2 t |
|
|
( |
|
|
|
) |
|
e |
|
1 t |
e |
|
2 t ; |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 t |
|
|
|
|
|
|
|
2 t |
|
1 |
|
2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
e |
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
e |
|
2 t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
' |
|
K0 |
[ |
|
' |
(0) |
b |
(0)] |
|
|
2 |
|
e |
2 t |
|
|
K0 |
[ |
' |
(0) |
b |
|
(0)] |
e |
2 t |
|||||||||
C1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
1 |
|
|
2 ) |
e |
1 t |
e |
2 t |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
K |
0 |
[ |
|
'(0) |
b |
(0)] |
e 1 t |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2

73
|
|
|
|
|
|
|
e |
|
|
1 t |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
' |
|
|
|
|
|
|
1 |
e |
|
1 t |
|
K0 |
[ |
' |
(0) b |
|
(0)] |
|
|
|
K0 |
[ |
' |
(0) |
b |
|
(0)] |
e |
|
1 t |
|||||||||||||||
C2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
1 |
|
|
|
2 ) |
e |
1 t |
e |
2 t |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
K |
0 |
[ |
|
|
'(0) |
|
b |
|
(0)] e 2 t |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Интегрируя полученные выражения, найдем варьируемые постоянные |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
C (t) |
|
|
|
K0 |
|
[ |
'(0) |
b |
|
(0)] |
|
e 1 tdt |
|
|
K0 |
( |
1 |
|
b) |
|
|
C ; |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
1 |
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
1 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
C (t) |
|
|
|
|
K0 |
|
|
|
|
[ |
|
'(0) |
b |
(0)] e 2 tdt |
|
|
|
|
K0 ( 2 |
b) |
C |
2 |
, |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где C1, C2 - новые постоянные интегрирования. Здесь при интегрировании |
|||||||||||||||||||||||||||||||||||||||||||||
учтено селектирующее свойство |
- функции и ее производной |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (t) |
(0) dt |
|
f (0) ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (t) |
'(0) |
|
dt |
|
|
f '(0) . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Подставим полученные значения C1(t) и C2 (t) в общее решение |
|||||||||||||||||||||||||||||||||||||||||||||
неоднородного дифференциального уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
v(t) ( |
K0 ( 1 |
b) |
C1) e |
1 t |
( |
K0 ( 2 |
|
b) |
C2 ) e |
|
2 t |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
K0 |
|
|
|
( 1 |
|
b) e |
1 t |
( 2 |
b) e |
|
|
2 t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C1 |
e |
1 t |
C2 |
e |
|
2 t |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Дифференцируя общее решение, находим выражение для его производной
|
|
|
|
|
|
|
1 ( |
1 |
b) e |
1 t |
|
2 ( 2 |
b) e |
2 t |
|
|
|
||||||||
|
v'(t) |
K0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
C |
1 |
e |
|
1 t |
|
C |
2 |
e |
2 t . |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Значения постоянных интегрирования C1 |
и |
C2 |
определим из |
||||||||||||||||||||||
начальных условий v(0) |
|
K0 |
и v'(0) |
K0 |
|
(0) |
[b |
( 1 |
|
|
2 )] |
|
, при t |
0 |
|||||||||||
v(0) |
K0 |
K0 |
C1 |
C2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||
v'(0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
0 |
(0) [b |
|
( |
1 |
|
2 |
)] |
K |
0 |
[b ( |
1 |
2 |
)] |
|
1 |
C |
2 |
C |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|||||||||
Перепишем данную систему в более удобном виде |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
C1 |
|
C2 |
|
0 |
|
|
|
|
(0) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
C1 |
|
2 |
C2 |
|
K0 |
|
|
|
|
|
|
|
|
|
|||
Определим постоянные интегрирования C1 и C2 , воспользовавшись правилом Крамера
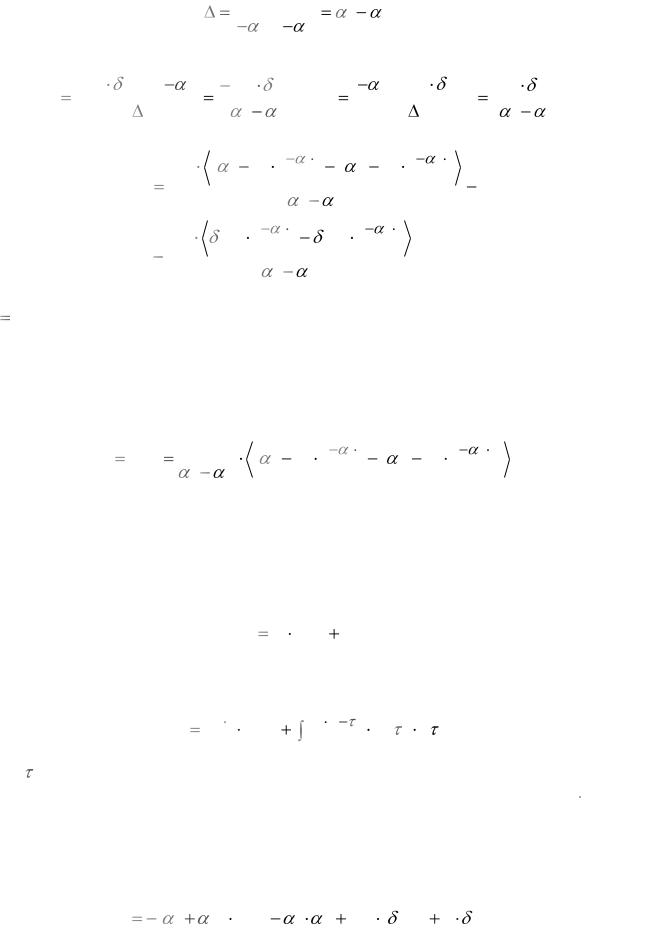
74
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
2; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
C1 |
|
K0 (0) |
2 |
|
K0 |
(0) |
; |
C2 |
|
|
1 K0 |
(0) |
|
K0 |
(0) |
. |
||||||||
|
|
|
|
1 |
2 |
|
|
|
|
|
1 |
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Подставляя найденные постоянные в общее решение, получаем |
|
|||||||||||||||||||||||
|
|
|
|
K0 |
( 1 |
|
b) e |
|
1 t |
( |
|
2 b) e |
2 t |
|
|
|||||||||
|
|
v(t) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
K0 |
(0) |
e |
1 t |
|
|
|
|
(0) |
|
e |
2 t |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2
Последнее слагаемое равно нулю, в силу того, что значения экспонент, при t 0 , равны по модулю единице и, следовательно, знаменатель второго слагаемого равен нулю.
Таким образом, частное решение дифференциального уравнения, соответствующее импульсной характеристике, исследуемой активной RC - цепи второго порядка с последовательной ООС и учетом начальных условий, принимает вид
v(t) g(t) |
K0 |
|
( |
1 |
b) e |
1 |
t |
( |
2 |
b) e |
2 |
t |
) . |
1 |
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Заметим, что полученное методом Лагранжа выражение совпадает с решением операторным методом.
Метод Коши – интегрирования дифференциальных уравнений.
Метод Коши позволяет, используя начальные условия, сразу записать частное решение дифференциального уравнения. Согласно методу Коши, решение системы дифференциальных уравнений первого порядка
|
|
Y '(t) |
A Y (t) F (t) , |
|
где |
Y (t), Y '(t), F (t) - в |
общем |
случае векторы |
функций; A- матрица |
коэффициентов, может быть представлено в виде или форме Коши |
||||
|
|
|
t |
|
|
Y (t) |
e A t Y (0) e A (t ) F ( ) |
d , |
|
|
|
|
0 |
|
где |
- параметр времени; Y (0) - |
начальное значение вектор-функции либо |
||
вектор начальных значений системы дифференциальных уравнений; eA t - в случае системы дифференциальных уравнений, экспонента от матрицы коэффициентов.
В данном случае исходное дифференциальное уравнение второго порядка имеет вид
v''(t) ( 1 2) v'(t) 1 2 K0 [ '(0) b (0)] .

75
Метод Коши, применительно к дифференциальным уравнениям выше первого порядка подразумевает предварительный переход к системе дифференциальных уравнений первого порядка путем введения новых переменных.
Для перехода от исходного дифференциального уравнения второго порядка к системе двух дифференциальных уравнений первого порядка введем новые переменные
y (t) |
y |
v(t) ; y |
y' |
v'(t) , то есть |
y' |
v''(t) . |
|
1 |
1 |
2 |
1 |
|
|
2 |
|
В результате приходим к системе вида |
|
|
|
||||
y1' |
0 |
1 |
|
y1 |
|
0 |
|
y2' |
1 2 |
( 1 |
2 ) |
y2 |
K0 [ |
'(0) |
b (0)] |
или |
|
|
|
|
|
|
|
|
|
Y '(t) |
A Y (t) F (t) , |
|
|
||
где
|
y1(t) |
v(t) |
' |
' |
(t) ; |
|
Y (t) |
; Y '(t) |
y1(t) |
v |
|
||
|
y2 (t) |
v'(t) |
y2' (t) |
v''(t) |
|
|
F (t) |
0 |
; A |
0 |
|
1 |
|
[ '(0) |
|
( 1 |
2 ) |
|||
K0 |
b (0)] |
1 2 |
||||
Для нахождения функций от матричного аргумента решить проблему собственных значений и векторов, то каноническое разложение матрицы коэффициентов
.
необходимо есть найти
A H H 1,
где - диагональная матрица собственных значений, либо матрица Жордана при наличии кратных собственных значений; H - модальная матрица собственных векторов.
Аналитическая функция от матрицы при различных собственных значениях определяется выражением
F ( A) H F ( ) H 1,
где F ( ) - диагональная матрица, в которой элементы есть данная функция
от собственного значения.
Для определения собственных значений воспользуемся характеристическим уравнением
det[ A |
] 0; |
|
|
1 |
|
2 |
( |
|
2 ) |
1 2 0. |
|
|
|
|
1 |
||||||
1 2 |
( 1 |
|
2 ) |
|
||||||
|
|
|
|
|
|
|
|
Как видим, характеристическое уравнение, определенное таким образом, полностью совпадает с характеристическим уравнением, полученным из передаточной функции.
Можно убедится, что корни характеристического уравнения или собственные значения равны

|
|
76 |
|
|
|
1 |
0 |
|
1 |
0 |
. |
|
|
|
|||
0 |
|
0 |
|
|
|
2 |
|
|
2 |
||
|
|
|
|
Собственные вектора hi , то есть столбцы модальной матрицы H находятся,
с точностью до постоянных, из решения однородных систем [ A |
i ] hi |
0 , |
по известны собственным значениям, где i - диагональная матрица с |
i |
|
значением по диагонали. Можно показать, что модальная матрица собственных векторов определяется следующим образом
H |
11( |
1) |
11( |
2 ) |
, |
12 ( |
1) |
12 ( |
2 ) |
где 1i ( j ) - алгебраические дополнения одной из строк характеристической
матрицы [ A |
j ] , например первой. |
|
|
|
|
|
|
|
|
|
|
|
||||
Раскрывая указанное соотношение, получаем модальную |
||||||||||||||||
собственных векторов в виде |
|
|
|
|
|
|
|
|
|
|
|
|
||||
H |
( 1 |
2 ) |
1 |
( 1 |
2 ) |
|
2 |
|
|
2 |
|
|
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
2 |
|
|
1 |
2 |
|
|
|
1 |
2 |
1 |
|
2 |
|
|
Определитель модальной матрицы равен |
H |
1 |
2 |
( 1 |
2 ) . |
|
|
|||||||||
Далее, найдем обратную модальную матрицу |
|
|
|
|
|
|
|
|||||||||
H 1 |
1 |
|
|
|
1 2 |
|
1 |
|
|
1 |
|
|
1 |
1/ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 2 ( 1 |
2 ) |
|
1 2 |
|
2 |
1 |
|
2 |
|
1 |
|
1/ 1 |
||||
|
|
|
|
|
|
|||||||||||
После этого выразим экспоненту от матрицы
матрицу
.
e A t H e t H 1 |
|
|
|
2 |
|
|
1 |
|
e |
1 t |
|
0 |
|
|
|
1 |
|
|
1 |
1/ |
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
1 |
|
2 |
1 |
2 |
|
|
0 |
e |
1 t |
|
1 |
2 |
|
|
1 |
1/ |
1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
eA t |
|
1 |
|
|
|
2 |
e |
1 t |
|
1 |
e |
2 t |
|
e |
1 t |
e |
2 t |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
2 |
|
1 2 (e |
1 t |
|
e |
2 t ) |
|
1 e |
|
1 t |
2 e |
2 t |
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
Отметим, что матрица eA (t |
) |
имеет аналогичную структуру. |
|
|
|
|
|
|||||||||||||||||
Учитывая тот факт, что вектор начальных |
условий Y (0) |
и вектор |
||||||||||||||||||||||
внешних воздействий F ( |
) |
имеют вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Y (0) |
y1(0) |
|
v(0) |
|
|
|
|
|
K0 |
|
|
|
|
|
; |
|
|
|
|
|||||
y2 (0) |
|
v'(0) |
|
K0 |
(0) [b |
|
( 1 |
2 )] |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F ( |
) |
|
|
|
'(0) |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
K0 |
[ |
b |
(0)] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
а также, то, |
что |
нас |
|
интересует |
первая |
компонента |
вектора |
решения |
||||||||||||||||
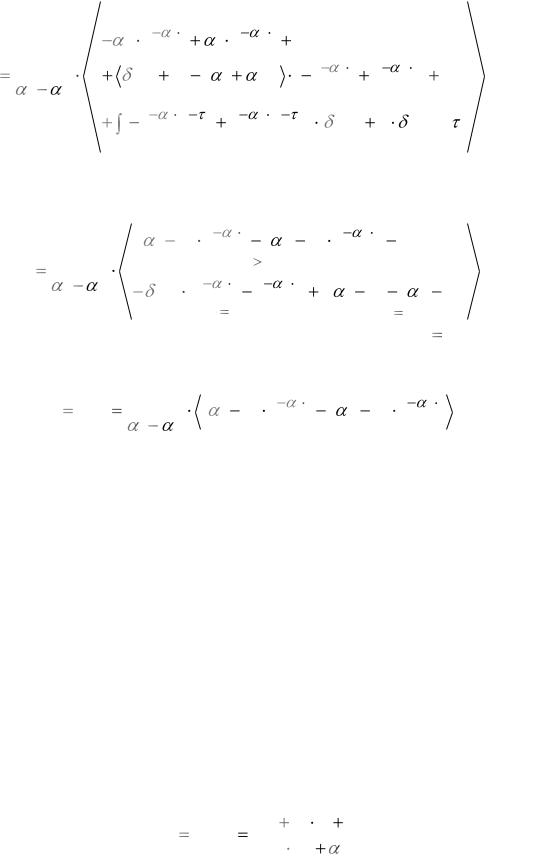
y1(t) v(t) , получаем из полной формулы Коши выражение для выходного напряжения в виде
77
|
|
|
2 |
e |
1 t |
|
1 |
e |
2 t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
v(t) |
K0 |
|
|
(0) |
[b |
( |
1 |
|
2 |
)] |
( e |
1 |
t |
e |
2 |
t |
) |
. |
1 |
2 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 (t |
) |
|
e 2 (t |
) ) [ |
'(0) |
|
|
|
|
|
||||
|
|
|
( |
e |
|
b |
|
(0)] d |
|
|||||||||
0
Раскрывая интеграл и, приводя подобные, получаем решение, соответствующее переходной характеристике, исследуемой активной RC - цепи второго порядка с последовательной ООС, в виде
|
|
[( |
1 |
b) e |
1 t |
( |
2 |
b) e |
2 t ] |
|
|
|
|
K0 |
|
|
|
|
|
|
|
||||
v(t) |
|
|
|
t 0 |
|
|
|
|
. |
|||
|
|
|
|
|
1 t |
|
2 t ) [( 1 |
|
|
|||
|
1 |
2 |
|
(0) (e |
e |
b) |
( 2 |
b)] |
||||
|
|
|
|
|
t |
0 |
|
|
|
t |
0 |
|
Учитывая, |
что вторая составляющая равна нулю при t |
0 и сращивая |
||||||||||
во времени первую и третью составляющие, окончательно получаем решение дифференциального уравнения в виде
v(t) g(t) |
K0 |
|
( |
1 b) e |
1 t |
( 2 b) e |
2 t |
. |
1 |
2 |
|
|
|||||
|
|
|
|
|
|
|
Как видим, полученное методом Коши решение совпадает с предыдущими решениями операторным методом и методом Лагранжа и представляет импульсную характеристику, исследуемой активной RC - цепи второго порядка с последовательной ООС, где в качестве реакции на единичный импульс на входе, рассматривается напряжение на выходе.
Таким образом, все три метода, предлагаемой методики исследования временных характеристик (операторный, Лагранжа и Коши), дают совпадающие результаты при их корректном применении.
В заключение отметим, что все нормированные характеристики, исследуемой активной RC - цепи второго порядка с последовательной ООС, совпали с характеристиками, ранее исследованной активной цепи второго порядка RLC - типа, поскольку цепи имеют аналогичные структуры канонических передаточных функций.
Аналоговая система, заданная выражением передаточной функции. Аналоговая система второго порядка задана передаточной функцией вида
|
p2 |
b p |
b |
|
KV ( p) K ( p) |
|
1 |
0 |
|
p |
( p |
) |
||
|
и требуется по предлагаемой методике определить ее временные характеристики.
Приравнивая знаменатель нулю, получаем характеристическое уравнение

78
p ( p |
) p2 |
|
|
p |
0, |
|
корни которого, соответственно, равны |
1 |
0 |
и |
2 |
. |
|
|
|
|
|
|
||
Распишем коэффициент передачи по напряжению через отношение выходного напряжения к входному воздействию
|
V ( p) |
|
p2 b |
p b |
||
K ( p) |
|
|
1 |
0 |
. |
|
E( p) |
p ( p |
) |
||||
|
|
|
||||
Из последнего выражения коэффициента передачи напряжения непосредственно получаем изображение выходного напряжения цепи, как выходной переменной и реакции цепи на входное воздействие
|
|
|
E( p) ( p2 |
b p b ) |
|
|
|
|
|
||
|
|
V ( p) |
|
1 |
0 |
. |
|
|
|
|
|
|
|
p ( p |
) |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
|
Найдем значения передаточной функции |
V ( p) |
K ( p) |
p V ( p) , при |
|||||||
|
|
E( p) |
|
||||||||
|
|
|
|
|
|
|
|
|
|||
p |
0 и p |
, принимая E( p) 1/ p . Так при p |
|
0 , получаем K (0) |
, а |
||||||
при |
p |
, имеем неопределенность |
вида |
/ . |
Раскрывая |
||||||
неопределенность по правилу Лопиталя, получаем K ( ) |
1. |
|
|
||||||||
Переходная характеристика. Определим несколькими способами переходную характеристику цепи. В качестве входного воздействия, в этом случае используется функция Хевисайда
E( p) 1/ p 1(t) e(t) .
Операторный метод. При воздействии на вход единичного скачка изображение выходного напряжения имеет вид
|
E( p) ( p2 |
b p b ) |
|
p2 |
b p b |
|||
V ( p) |
|
1 |
0 |
|
|
1 |
0 |
. |
p ( p |
|
) |
|
p2 |
( p |
) |
||
|
|
|
|
|||||
Используя таблицы обратного преобразования Лапласа, устанавливаем соответствие между изображением и оригиналом
p2 |
b1 p |
b0 |
|
1 |
( b1 |
b0) |
b0 t ( |
2 |
b1 b0) e |
t |
. |
p2 |
( p |
) |
2 |
|
|
||||||
|
|
|
|
|
|
|
|||||
На основании установленного соответствия, находим оригинал выходного напряжения, соответствующий переходной характеристике, исследуемой аналоговой системы второго порядка
|
p2 |
b p |
b |
|
|
|
|
|
|
|
|
||
V ( p) |
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
|
p2 |
( p |
) |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
( |
b b ) |
b t ( 2 |
b b ) e t |
v(t) h(t) . |
||||||
|
|
|
|
||||||||||
|
|
|
|
||||||||||
|
2 |
|
|
1 |
0 |
|
0 |
1 |
0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
Отметим, |
что |
начальное |
значение |
переходной |
характеристики, при |
||||||||
t 0 , равно единице |
h(0) |
1, |
а установившееся |
значение переходной |
|||||||||
характеристики, при t |
|
, равно бесконечности h( ) |
. |
|
|||||||||

79
Как видим, в соответствии с теоремами операционного исчисления о начальном и конечном значении функции, выполняются соотношения вида
v(0) |
h(0) |
|
lim |
p V ( p) |
lim K ( p) |
1; |
|
||||||||
|
|
|
|
|
|
p |
|
|
|
p |
|
|
|
|
|
v( ) |
h( ) |
|
lim |
p V ( p) |
lim K ( p) |
. |
|
||||||||
|
|
|
|
|
|
|
p 0 |
|
|
p |
0 |
|
|
|
|
Выразим производную от выходной реакции |
|
|
|
||||||||||||
v'(t) h'(t) |
1 |
|
|
|
|
b |
|
( 2 |
|
b b ) e t |
|
||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
|
|
|
0 |
|
|
|
1 |
0 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
b |
|
( |
2 |
b |
b ) |
e t |
|
|
|||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
0 |
|
|
1 |
|
0 |
|
|
|
|
и отметим, что значение производной, при |
t |
0 , |
равно |
h'(0) b |
, а при |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
t, равно h'( ) b0 / .
Заметим, что переходная характеристика, исследуемой аналоговой
системы второго порядка, имеет более сложный вид, по сравнению с характеристиками цепей первого порядка.
Далее, переходим к формированию дифференциального уравнения с целью получения переходной характеристики путем его аналитического интегрирования.
Формирование и интегрирование дифференциального уравнения.
Дифференциальное уравнение цепи относительно выходного напряжения, как и в предыдущем случае, формируем на основе его операторного выражения, путем замены изображений оригиналами, а оператора Лапласа p
оператором дифференцирования d / dt .
Так, используя операторное выражение для изображения выходного напряжения и, учитывая, что в данном случае E( p) 1/ p , получаем
|
|
|
|
|
2 |
|
|
|
1(t) |
[( |
|
d |
) |
2 |
|
b |
|
d |
|
b ] |
|
||||||||||
|
|
|
E( p) ( p |
b1 p b0 ) |
|
dt |
|
|
|
|
dt |
|
|||||||||||||||||||
V ( p) |
|
|
v(t) |
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
|
|
|||||||||||||
|
|
p ( p |
) |
|
|
|
|
|
d |
|
|
|
|
( |
|
d |
) |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
dt |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
1(t) |
[( |
|
|
d |
|
) |
2 |
|
b |
|
d |
b ] |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
1 |
|
dt |
0 |
|
|
, |
|||
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
d |
|
|
) |
2 |
|
|
|
d |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
dt |
|
|
|
|
||||
где 1(t) |
1/ p - единичный скачок или функция Хевисайда, |
как результат |
|||||||||||||||||||||||||||||
обратного преобразования Лапласа от 1/ p в области изображений. |
|
||||||||||||||||||||||||||||||
Перегруппировывая |
полученное |
выражение |
|
|
|
|
и, |
|
учитывая, что |
||||||||||||||||||||||
d (1(t)) / dt |
|
(0) |
и |
|
d 2 (1(t)) / dt2 |
|
' (0) , |
приходим |
|
|
|
к |
записи |
||||||||||||||||||
дифференциального уравнения относительно выходного напряжения, исследуемой аналоговой системы второго порядка
v''(t) |
v'(t) |
'(0) b |
(0) b . |
|
|
1 |
0 |

80
Дифференциальное уравнение цепи относительно выходного напряжения можно получить также из коэффициента передачи по напряжению, путем замены изображений входного воздействия и реакции оригиналами, а оператора Лапласа p оператором дифференцирования d / dt .
Так, используя операторное выражение для изображения коэффициента передачи напряжения, получаем
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
( |
d |
) |
2 |
|
b |
|
d |
b |
||||
|
|
|
|
|
|
V ( p) |
|
|
|
V ( p) |
p |
b1 |
p b0 |
|
v(t) |
dt |
|
|
|
dt |
||||||||||||||
K ( p) |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
0 |
|
||||||||||||||||||
|
|
E( p) |
|
|
|
|
1/ p |
|
|
|
p ( p |
) |
|
1(t) |
|
|
|
|
d d |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
dt |
|
|
|||||
( |
|
d |
) |
2 |
|
b |
|
d |
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
dt |
|
|
|
1 |
|
dt |
0 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
( |
d |
) |
2 |
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
dt |
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Перегруппировывая |
полученное |
выражение |
|
и, |
учитывая, что |
|||||||||||||||||||||||||||||
d (1(t)) / dt |
|
|
(0) |
и |
|
|
d 2 (1(t)) / dt2 |
' (0) , |
приходим |
|
к |
|
той |
же форме |
||||||||||||||||||||
дифференциального уравнения относительно выходного напряжения, исследуемой аналоговой системы второго порядка
v''(t) |
v'(t) |
'(0) b |
(0) b . |
|
|
1 |
0 |
Данное уравнение является неоднородным обыкновенным дифференциальным уравнением второго порядка. В нормальной форме Коши, уравнение, разрешенное относительно старшей производной, имеет вид
v''(t) |
v'(t) |
'(0) b |
(0) b . |
|
|
1 |
0 |
Прежде, чем приступить к интегрированию полученного неоднородного обыкновенного дифференциального уравнения, с целью получения частного решения, необходимо определить начальные условия v(0) и v'(0) .
Определение начальных условий. Для определения начальных условий удобно воспользоваться теоремой операционного исчисления о начальном значении функции оригинала
|
|
|
|
|
|
|
|
|
|
p2 |
b |
p |
b |
|
|
|
|
|
v(0) |
lim v(t) |
lim p V ( p) |
lim |
|
1 |
|
0 |
1 |
; |
|
||||||
|
p ( p |
|
) |
|
|||||||||||||
|
|
t 0 |
|
p |
|
|
|
p |
|
|
|
|
|
||||
' |
|
' |
|
|
|
2 |
|
|
|
p ( p2 |
b1 p b0 ) |
||||||
v |
(0) |
lim v |
(t) |
lim |
p |
|
V ( p) |
lim |
|
|
|
|
|
|
|
|
|
|
|
|
p ( p |
) |
|
|
|
|
|||||||||
|
t |
0 |
|
p |
|
|
|
p |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
p2 |
b |
p |
b |
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
1 |
|
0 |
|
|
. |
||
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
||||
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
||
Заметим, что первое начальное значение, совпало с ранее найденным |
|||||||||||||||||
значением переходной, при t |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||
