Устройства СВЧ и антенны

Таблица П.1.3

Значения удельной проводимости некоторых веществ при t=20 °С

ПРИЛОЖЕНИЕ 2

П.2. Значения корней функции Бесселя []

Таблица П.2.1

ПРИЛОЖЕНИЕ 3

П.3. ФИЛЬТРЫ СВЧ

П.3.1Классификация фильтров

Идеальным фильтром называется четырехполюсник, модуль коэффициента передачи которого S21 равен единице на всех частотах, образующих его

полосу пропускания, и равен нулю на всех частотах, образующих его полосу заграждения. На практике фильтры обычно характеризуют вносимым затуханием (выраженным в децибелах):

В полосе пропускания идеального фильтра Lф = 0, а в полосе заграждения Lф=∞. По взаимному расположению полос пропускания и заграждения фильтры делятся на фильтры нижних частот (ФНЧ), фильтры верхних час-

тот (ФВЧ), полосовые фильтры (ПФ) и режекторные (заграждающие)

фильтры (РФ). Амплитудно-частотные характеристики идеальных фильтров каждого типа показаны на рис. П.3.1. В идеальных фильтрах в полосе

214

заграждения мощность, поданная на вход, не проходит на выход. Она либо полностью отражается от входа фильтра, либо поглощается в его элементах. В первом случае фильтры относятся к фильтрам отражающего типа, во втором - к фильтрам поглощающего типа. Отметим, что полная величина вносимых фильтром потерь складывается из тепловых потерь и потерь, вызванных отражением части энергии от его входа.

Рассмотрим фильтры отражающего типа. Для уменьшения тепловых потерь такие фильтры выполняются, как правило, из реактивных элементов. Параметры реактивных элементов подбираются так, чтобы на частотах полосы пропускания отраженные от них волны компенсировали друг друга на входе фильтра; при этом мощность, поступающая на вход фильтра, проходит на его выход практически без отражений. На частотах полосы заграждения компенсация отраженных волн отсутствует и мощность, поступающая на вход фильтра, практически полностью отражается от него.

Синтез фильтров отражающего типа включает два основных этапа: на первом этапе по исходным данным синтезируют эквивалентную схему фильтра, состоящую из реактивных элементов с сосредоточенными параметрами; на втором этапе проводят реализацию синтезированной эквивалентной схемы, т.е. заменяют сосредоточенные индуктивности и емкости отрезками линий передачи, реактивными стержнями и диафрагмами и другими неоднородностями в линии передачи. В технике СВЧ широкое применение получили так называемые лестничные отражающие фильтры. Эквивалентные схемы таких фильтров совпадают со схемой лестничных фильтров, используемых на низких частотах и выполняемых из элементов L и С с сосредоточенными параметрами; подобные схемы подробно рассматриваются в курсе "Теория линейных электрических цепей" .

П.3.2. Синтез эквивалентных схем фильтров

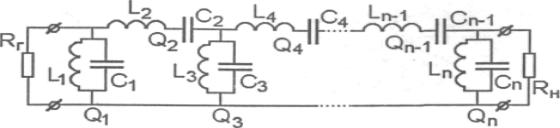
Рассмотрим синтез эквивалентной схемы ФНЧ, выполненной по лестничной схеме. Такая схема, состоящая из п элементов L и С, показана на рис. П.3.2. Внутреннее сопротивление Rr генератора, подключенного ко входу схемы, и сопротивление RH нагрузки на ее выходе считаем активными и равными друг другу.

215

Отметим, что во многих практических приложениях главное значение имеет АЧХ фильтра. Ниже рассматривается синтез эквивалентных схем фильтров по заданной АЧХ.

Идеальную АЧХ для ФНЧ (рис. П.3.1,а) невозможно получить с помощью схемы, имеющей конечное число элементов n. Поэтому обычно используют более приемлемый для практики способ задания требований к АЧХ: в диапазоне частот 0<f<fc (полоса пропускания) величина вносимого затухания не должна превышать заданную величину LФ1, а в полосе f3<f<<x> (полоса заграждения) вносимое затухание должно быть больше

заданной величины Lф2 (рис. П.3.3). Указанную идеализированную АЧХ аппроксимируют той или иной функцией.

Наибольшее распространение на практике получили два вида аппроксимации: максимально плоская и чебышевская. В первом случае вносимое затухание для n-звенного фильтра описывается функцией, предложенной Баттервортом [16]:

где h = 10Lф1/10-1, а для ФНЧ Ω= f/fc. Зависимость Lф от f для разных n показана на рис. П.3.4, а. Как следует из рисунка, при f«fc Lф 0 и не зависит от частоты. Подобная АЧХ максимально приближена к идеальной АЧХ в полосе пропускания, отсюда и ее название - максимально плоская АЧХ. При фиксированных величинах fс, LФ1 и fз увеличение числа элементов в схеме n приводит к возрастанию

216

величины LФ2 (см. рис. П.3.4,а) или при фиксированных величинах fc, LФ1 и Lф2-к уменьшению разницы между f3 и fс, т.е. увеличивается крутизна АЧХ.

Во втором случае АЧХ фильтра аппроксимируется с помощью полиномов Чебышева [16]:

где Тn(х)- полином Чебышева первого рода порядка п, описываемый выражениями

217

Типичная чебышевская АЧХ фильтра нижних частот показана при разных п на рис. П.3.4, б. В полосе пропускания подобная АЧХ имеет осциллирующий характер с неизменной амплитудой осцилляции. Увеличить крутизну АЧХ при неизменной амплитуде осцилляции можно, лишь используя схему, с большим числом элементов п. Основное преимущество чебышевских фильтров по сравнению с максимально плоскими-меньшее число элементов в схеме при одинаковых значениях LФ1, LФ2, fc и fз.

Отметим, что при передаче через фильтр электромагнитных сигналов с достаточно широким спектром частот (широкополосные сигналы) важное значение имеет вид фазочастотной характеристики (ФЧХ) фильтра; ФЧХэто зависимость аргумента q>21 коэффициента передачи фильтра S21 = lS21|exp(ij21) от частоты. Предполагается, что у идеального фильтра ФЧХ является линейной функцией частоты. При этом широкополосный сигнал проходит через такой фильтр без искажений. При одинаковых исходных данных ФЧХ максимально плоского фильтра более близка к линейной, чем аналогичная характеристика чебышевского фильтра.

Из (П.3.2) и (П.3.3) можно получить следующие формулы для определения числа звеньев в схеме фильтра: для максимально плоского фильтра

для чебышевского фильтра

где для ФНЧ Q3 = f3/fc- Обычно при вычислениях по (14.8) используют тождество

arch (x) = ln (x + Öx2-1).

На практике, как правило, синтез эквивалентных схем фильтров разных типов проводят с помощью синтеза схемы фильтра-прототипа нижних частот. Схема такого фильтра совпадает со схемой ФНЧ (рис.П.3.2) и имеет такое же число звеньев, а параметры его элементов обозначаются буквами q1, q2,.. qn (q0 и qn+1 соответствуют активным сопротивлениям генератора и нагрузки). Эти параметры (иногда их называют q-параметрами) являются нормированными параметрами элементов ФНЧ, так как они равны параметрам элементов ФНЧ при wс = 1 рад/с и RH=Rr=1 Ом. Для фильтра-прототипа q-параметры определяют по следующим формулам:

для максимально плоского фильтра

218

где a j = sin[(2j-1)p/(2n)], bj = y2 + sin2(jn/n), y = sh [p/(2n)], p= ln[сth(Lф1/17,37)].

Отметим, что для максимально плоских фильтров элементы с одинаковыми значениями q в схеме (рис.П.3.2) расположены симметрично относительно середины фильтра как для четных, так и для нечетных значений п. Поэтому ко входу и выходу фильтра должны подключаться одинаковые сопротивления

qo=qn+1.

Рис. П.3.5

Для чебышевских фильтров указанное свойство выполняется лишь для нечетного числа звеньев в схеме, при п четном симметрия нарушается и получается q0¹ qn+1. При необходимости подключения одинаковых сопротивлений ко входу и выходу чебышевского фильтра с четным числом звеньев (например, если фильтр встраивается в линию передачи с заданным волновым сопротивлением) следует включить в схему такого фильтра дополнительный трансформатор сопротивлений.

Исходными данными при синтезе эквивалентной схемы ФНЧ являются следующие величины (рис. П. 3.3): fc, fз, Lф1, Lф2, RH и вид АЧХ. Вначале с помощью исходных данных вычисляют по (П.3.4) или (П.3.5) число звеньев в эквивалентной схеме фильтра. Затем по формулам (П.3.6) или (П.3.7) рассчитывают q- параметры элементов схемы фильтра - прототипа. Для получения формул, связывающих величины индуктивностей и емкостей эквивалентной схемы ФНЧ с q- параметрами, приравняем нормированные проводимости (умноженные на RH) элементов, образующих параллельные ветви схемы, и нормированные сопротивления (деленные на RH) элементов, образующих последовательные ветви схемы, проводимостям и сопротивлениям соответствующих элементов фильтрапрототипа:

219

Рассмотрим синтез эквивалентной схемы ПФ, выполненной по лестничной схеме. Такая схема, состоящая из п последовательных и параллельных контуров из L и С, изображена на рис. П.3.5. И в этом случае при синтезе эк-

вивалентной схемы используют идеализированную АЧХ (рис. П.3.6), для которой в полосе пропускания фильтра fH£f£fB вносимое затухание Lф£Lф1, а в полосе заграждения f£f31 и f³f32 вносимое затухание

Lф³ Lф2. Для максимально плоской аппроксимации этой АЧХ используется функция (П.3.2), а для чебышевскойфункция (П.3.3), в которой необходима следующая замена частотной переменной:

Следует отметить, что при замене (П.3.10) АЧХ фильтра-прототипа переходит в АЧХ полосового фильтра (на рис. П.3.7) показано преобразование максимально плоской АЧХ).

Исходными данными при синтезе эквивалентной схемы ПФ (см. рис. П.3.6) являются следующие величины: fH, fB, f31, f32, LФ1, LФ2, RH и вид АЧХ. Вна-

схеме фильтра, равное числу элементов в схеме фильтра-прототипа. Затем по формулам (П.3.6) или (П.3.7) рассчитывают q-параметры элементов схемы фильт- ра-прототипа. Действуя, как и в случае синтеза эквивалентной схемы ФНЧ, несложно получить следующие формулы для расчета параметров элементов контуров эквивалентной схемы ПФ через q-параметры фильтра-прототипа:

в случае параллельных контуров

L2 j−1 = R H (fB − fH ) /(2pf02q2 j−1 ) [Гн],C2 j−1 = q2 j−1 /(R H 2p(fB − fH ) [Ф]

(П.3.11)

а для последовательных контуров

220

L2 j = q2 jR H /[2π(fB − fH )][Гн],C2 j = (fB − fH ) /[2πf02q2 jR H ][Ф], (П.3.12)

где j=1,2 .…, т; т=n/2 при четном n и m = (n + 1)/2 при нечетном n; f02 = f B − f H .

Нагруженная добротность контуров эквивалентной схемы ПФ определяется по формуле [16]:

Аналогичным образом, используя результаты синтеза фильтрапрототипа и выбирая соответствующую замену частотной переменной в аппроксимирующей функции для АЧХ, синтезируются эквивалентные схемы фильтров верхних частот и режекторные фильтры [16].

Реализация эквивалентных схем фильтров СВЧ. В диапазоне СВЧ,

как правило, фильтры строят из элементов с распределенными параметрами. При этом схемы, состоящие из элементов с сосредоточенными параметрами, рассматриваются как эквивалентные схемы. Синтезировав эквивалентную схему фильтра, как было показано выше, выполняют второй этап проектирования - реализуют полученную эквивалентную схему. Вначале пытаются с помощью элементов с распределенными параметрами смоделировать поведение сосредоточенных элементов эквивалентной схемы. Однако такой подход к синтезу конструкции СВЧ фильтра является лишь начальным и весьма грубым приближением, поскольку при этом не учитывается ряд важных факторов, влияющих на АЧХ синтезированной конструкции: периодичность частотных характеристик элементов с распределенными параметрами, дисперсия в отрезках линии, влияние неоднородностей в полученной конструкции и т.д. Поэтому получаемую вначале конструкцию рассматривают как первое или начальное приближение при реализации. Затем для полученной конструкции строят уточненную эквивалентную схему, пытаясь учесть ее особенности (влияние неоднородностей, дисперсию и тепловые потери в отрезках линии и т.д.). Уточненная эквивалентная схема позволяет реализовать конструкцию фильтра во втором приближении и т.д.