Устройства СВЧ и антенны

152

гласующего устройства изображен на рис. 5. 18,б.

Пластинчатый диэлектрический трансформатор. Двухшайбовый трансформатор полных сопротивлений в коаксиальной линии (см. рис. 5.19). На рисунке λ-длина волны в свободном пространстве

Можно показать, что максимальная величина КСВ=(εопт)2, при которой возможно согласование, равна квадрату относительной диэлектрической проницаемости вещества, из которого изготовлены пластины трансформатора.

Согласование с помощью конических переходов и вкладышей экспоненциального профиля. 1. Отрезки неод-

нородных передающих линий СВЧ, коконический переход - для согласования волноводных и коаксиальных линий с различными эквивалентными и характеристическими сопротивлениями. Основным достоинством его является широкополосность.

2. Экспоненциальный трансформатор, представляющий собой передающую линию, характерное или эквива-

лентное сопротивление которой измеряется по экспоненциальному закону. Прямоугольные волноводы, имеющие одинаковые размеры а и разные узкие сечения b1 и b2 согласовываются с помощью металлических вкладышей экспоненциального профиля (рис. 5.20).

Вопросы широкополосного актуальны особенно с разработкой ламп с большим диапазоном механической и электронной настройки: клистронов, магнитофонов, ЛБВ.

Широкополосное согласование с

реактивными нагрузками. Можно показать, что, если, нагрузка представлена в виде последовательного соединения активного сопротивле-

154

Обычно такие схемы замещения могут быть использованы в окрестности узла или пучности напряжения нагруженной линии передачи.

Пример 1 Определить возможную полосу согласования, если, допустим, КБВ

1/ρ=0,8, а нагрузка представляется последовательным колебательным контуром с добротностью Qн = 2.8 .

Решение. По формуле (5.38) полоса согласования

таким образом, полоса согласования не может быть больше 60%. При ШС согласующий 4-х-полосник

представляет собой многоэлементную схему, причем, чем больше число выбранных элементов, тем лучше характеристика согласования. Однако, существенно влияют на изменения характеристики согласования лишь начальные согласующие элементы. Обычно один или два элемента дают удовлетворительную характеристику согласования, и нет смысла усложнять со-

гласующий 4-х-полосник. Методику расчета простейшего СУ и его характеристику рассмотрим на примере согласования нагрузки с помощью одного элемента (резонансного контура).

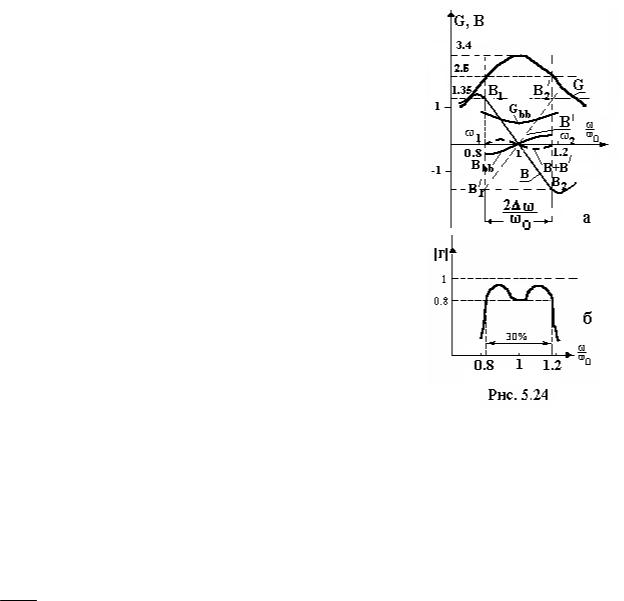
Пример 2. Согласовать ЛП, нагруженную на нормированную частотнонезависимую нагрузку

Zн = 1.8 - j ×1.46 в полосе 2 ω = 30% .

ω0

Решение. Рассматриваемая задача может быть решена согласованием в сечении а-а (рис. 5.23) последовательного резонансного контура с нормирован-

C/ . Такой контур имеет зависимость реактивной проводимости

Потребуем, чтобы на крайних частотах полосы ω1=0,85·ω0; и ω2=1,15·ω0, проводимости последовательного контура B1=1,45 и B2=-1,35 были равны проводимостям параллельного контура, взятым с обратным знаком B1=-В/1;

B2= -В/2).

Отсюда получим резонансную частоту параллельного резонансного контура ω/0 (она в общем случае не одинакова с ω) как точку пересечения линии В'1 В'2 с осью абсцисс. Получим ω0'=1,01·ω0. По наклону кривой реактивной проводимости В' определим индуктивность контура L'.

Таким образом, определены элементы компенсирующего контура. В результате включения этого контура проводимость в сечении а-а в полосе

2 ω = 30% , равная В+В', практически 0. Однако, активная составляющая

ω0

проводимости в заданной полосе отлична от волновой проводимости линии Yл=1 и, как видно из рис. 5.24,а, изменяется от 2,6 до 3,4. Чтобы согласовать активную проводимость, включим в сечение а-а четвертьволновый трансформатор с волновой проводимостью, лежащей между 1.62 и 1.84, так как

156

1 × 2.6 = 1.62

Yтр = Yл × Yaa = × =

1 3.4 1.84

Возьмем Yтр=1,62·L. Перечитав с помощью круговой диаграммы проводимости из сечения а-а в сечение в-в, получим зависимости активной составляющей GВВ и реактивной BВВ на входе транзистора. Итак, получено, что в

диапазоне частот 2 ω = 30% активная входная проводимость близка к еди-

ω0

нице, а реактивная к 0.

По ним с использованием круговой диаграммы рассчитывается характеристика согласования, представленная на рис. 5.24,б. Видно, что допустимый КБВ получился равным 0,8. Максимальная достижимая полоса при таком

КБВ 2 ω = 60% .

ω0

Согласование с помощью фильтров СВЧ. Этот раздел дается в при-

ближении [13], так как в приложении данного пособия приводится расчет фильтров, предложенный [13]. Затухание, вносимое фильтром отражающего типа на любой частоте, определяется в основном отражением потока энергии от его входа. Для фильтра отражающего типа частотная зависимость коэффициента отражения от входа имеет вид АЧХ вносимого затухания (см. рис. П.3.4). На этом основании фильтры отражающего типа применяют для согласования комплексных нагрузок с линией передачи. При этом реактивное сопротивление нагрузки рассматривается как последний элемент эквивалентной схемы полосового фильтра. Полоса пропускания фильтра является полосой согласования нагрузки с линией передачи. Предположим, что требуется согласовать линию передачи с волновым сопротивлением ZB с нагрузкой ZH, эквивалентная схема которой показана на рис. 5.25. В данном случае согласующим

устройством, включаемым между линией и нагрузкой, является полосовой фильтр, последний параллельный контур эквивалентной схемы которого образован емкостью нагрузки Сn и подключаемой ей параллельно индуктивности Ln. Величина Ln определяется с помощью формулы 2πf0 = 1 / Ln Cn где f0- средняя

частота требуемой полосы согласования. Поскольку Сn и RH заданы, то последний контур эквивалентной схемы полосового фильтра должен иметь при этом

схеме полосового фильтра Q1, Q2, ....., Qn-1 следует определять из условия получения полосового фильтра с требуемой АЧХ (П.3. 12.13), причем последний контур эквивалентной схемы фильтра имеет заданную добротность. Но как видно из (П. 3.12.13), (П. 3.6 и П. 3.7), добротность каждого контура эквивалентной схемы фильтра однозначно связана с полосой пропускания fB-fH и величиной Lф1 или соответствующей ей максимальной величиной коэффициента отражения Гmax от входа фильтра в этой полосе. Поэтому если добротность хотя бы одного контура задана, то между полосой пропускания фильтра и величиной Гтах существует вполне определенная связь, естественно разная для фильтров с разными видами АЧХ. Например, для максимально плоского полосового фильтра, используя приведенную здесь формулу для Qn, а также формулы (П.3.13) и (П.3.7), можно записать выражение

Из (5.40) вытекает, что при заданной комплексной нагрузке, чем меньше величина BФ1 (чем меньше Гmax), тем уже полоса согласования и наоборот. Как показано в [14], для каждой комплексной нагрузки существует максимально достижимая полоса согласования, зависящая от требуемого уровня согласования. Эта полоса тем больше, чем ниже уровень согласования, и наоборот.

6.МАТРИЧНЫЙ АНАЛИЗ МНОГОПОЛЮСНИКОВ СВЧ

6.1Многополюсники и их классические матрицы

Многополюсником называется устройство, имеющее несколько входов в виде поперечных сечений, подходящих к нему линий передач с заданными типами волн в каждой линии. Входы многополюсника называют также плоскостями отсчета фаз или плечами многополюсника. Чаще всего имеют дело с одномодовым режимом во входных сечениях, при котором в каждой линии передачи можно учитывать лишь один тип волны. Это достигается соответствующим удалением входных сечений от непосредственно многополюсника, так чтобы высшими типами волн, возникающих на соединении линии передачи с многополюсником, во входных сечениях можно было пренебречь. В этом случае число входов многополюсника равно числу подходящих к нему линий.

В матричной форме система (6.1) может быть представлена в виде

где [ U ] и [ I ] – векторы – столбцы входных напряжений и токов, [ Z ] – квадратная матрица сопротивлений.

158

Элементы матрицы [ Z ] называются собственными и взаимными сопротивлениями и предполагаются независящими от значений токов и напряжений. Поэтому связь между U и I описывается системой линейных уравнений, а сам многополюсник называется линейным.

В дальнейшем будем рассматривать только линейные многополюсники. Аналогично, может быть составлена система уравнений для определения входных токов через входные напряжения, которая в матричной форме может быть представлена в виде

В случае четырехполюсников применяется также классическая матрица передачи, которая связывает входные напряжение и ток с их выходными значениями

Очевидно, матрица передачи может быть составлена только для четырехполюсников, в то время как матрицы [ Z ] и [ Y ] - для любого 2N-полюсника. Матрицы [ Z ] и [ Y ] обычно применяются при последовательном и параллельном соединении многополюсников, так как в этих случаях общая матрица получается как сумма матриц, аналогично суммированию обычных сопротивлений и проводимостей.

Можно показать, что при каскадном включении четырехполюсников общая матрица передачи равна произведению их матриц передачи.

6.2.Волновые матрицы многополюсников

Вдиапазоне СВЧ непосредственное измерение входных напряжений и токов во многих случаях оказывается затруднительным. Более удобным является измерение амплитуд и фаз падающих и отражённых волн, например, с помощью измерительных линий. Поэтому в СВЧ диапазоне многополюсники характеризуются другими матрицами – рассеяния [S] и передачи [t] ( последняя только для четырехполюсников)

Очевидно, что напряжения U и токи I на входах многополюсника можно представить как сумму напряжений и токов падающих и отражённых волн

159

в линиях передачи, подключённых к многополюснику. Например, для входа 1 можно записать

U1 = U1П +U10 I1 = I1П + I10 . (6.8)

Напряжение и ток в падающей и отражённой волнах связаны между собой через волновое сопротивление данной линии, причём

Знак минус в последнем соотношении связан с изменением направления распространения отражённой волны по сравнению с падающей. Подставляя соотношения (6.9) в формулу для I1 из (6.8), получим

Таким образом, вместо величин U1 и I1 можно рассматривать связанные с ними U1П и U10. Проделав эту операцию по всем входам, мы совершим, таким образом, замену переменных в уравнениях типа (6.1) или (6.4): UI и II заменим на UIП и UI0 . При этом нужно помнить, что падающими называются волны, идущие к многополюснику, отражёнными – уходящие от него (рис.6.2).

U2 П

U20 2

напряжений, как на рис.6.1, а направление распространения волн. Вектор E в этих волнах, определяющий перенос энергии в линиях передачи, конечно, направлен поперек этих линий. Соотношения между напряжениями падающих и отражённых волн на входах многополюсника могут принимать различные формы, но наиболее распространённой является связь через матрицу рассеяния

Для четырехполюсников часто применяется другая форма связи UП и U0

– через волновую матрицу передачи [t].

Как и классическая матрица передачи, матрица [t] применяется при каскадном соединении четырехполюсников.

Выясним физический смысл коэффициентов матрицы [S]. Из первых двух уравнений системы (6.10) следует, что

Таким образом, S11 есть коэффициент отражения от первого входа многополюсника, при условии, что во всех других плечах отсутствуют падающие волны. Реально это достигается, если к первому плечу подключить генератор и измерить коэффициент отражения, при условии, что остальные плечи нагружены на согласованные нагрузки, равные волновым сопротивлениям соответствующих линий.

Соответственно, S21 есть волновой коэффициент передачи по напряжению из первого плеча во второе при тех же условиях эксперимента. Очевидно, это справедливо и для других плеч. Таким образом, Sii есть коэффици-

ент отражения по напряжению от i-ого плеча, при согласованных остальных, Sik – волновой коэффициент передачи по напряжению из k-ого плеча в i-ое, при согласовании всех свободных плеч.

Коэффициенты матрицы [S] имеют чёткий физический смысл, а их экспериментальное определение вполне возможно. Это является основным положительным качеством матриц рассеяния. Коэффициенты матрицы [t], в основном, не имеют чёткого физического смысла и обычно определяется через Sik. Связь между коэффициентами матриц [S] и [t] легко устанавливается из соотношений:

Она может быть представлена в виде: