Радиотехнические системы передачи информации

123

символа, выбранное таким способом, называется максимально правдоподобным. Чтобы при приеме серии импульсов каждый раз не определять М расстояний, следует заранее плоскость CS разбить на М частей, соответствующих каждому из сигналов (пример такого разбиения штриховыми линиями для сигнала с КАМ-16 дан на рис. 5.3).

Рис. 5.3. Подмножества, соответствующие каждому из сигналов КАМ-16

Существуют ошибки М(М–1) видов, причем, в отличие от двоичного случая, ошибки разных видов неравновероятны. Поскольку нормальная двумерная совместная плотность вероятности шумовых составляющих координат точки (v1,v2) имеет круговую симметрию, из всех возможных видов ошибки наиболее вероятно попадание точки, соответствующей принятому сигналу с шумом, в соседнюю область (по горизонтали либо по вертикали). При этом чаще возникают ошибки при демодуляции сигналов, которым соответствуют внутренние точки на диаграмме типа изображенной на рис. 5.3 (у них больше соседей).

Тогда точное и приближенное (с некоторым превышением) выражения для полной вероятности ошибки при демодуляции принимаемого импульса

где p 1 Ô( q / 2) – вероятность ошибки (5.13) при демодуляции двоичного ФМ сигнала,

q2 – отношение энергии разности двух ближайших сигналов к спек-

тральной плотности шума.

Для двукратной и трехкратной ФМ (рис. 2.18) при q >4…6 формула для полной вероятности ошибки имеет следующий вид:

Очевидно, что увеличение битовой скорости передачи, которое достигается при использовании многопозиционных методов модуляции, потребует существенного увеличения средней энергии полезного сигнала на входе приемника, пропорциональной величине qc2. Здесь частотная эффективность

124

системы улучшается за счет снижения ее энергетической эффективности.

В таблице 5.1 приведены значения отношения qc q 2 для разных видов мо-

дуляции.

В заключение отметим, что при использовании многопозиционных методов модуляции BER зависит еще и от способа кодировки возможных зна-

Таблица 5.1. Значения отношения qc q 2

чений М-ичного символа при помощи k-разрядных двоичных комбинаций. Наилучшим является такой код, когда соседним значениям импульса соответствуют комбинации, отличающиеся лишь в одном символе. Коды, показанные на рис. 2.18б и 2.18в, не удовлетворяют этому требованию. В частности, при использовании трехкратной ФМ для преобразования восьмиричной цифры в двоичную комбинацию существует код Грея (0↔000; 1↔001; 2↔011; 3↔010; 4↔110; 5↔111; 6↔101; 7↔100). Здесь при возникновении наиболее вероятных ошибок из трех битов комбинации ошибочным оказывается лишь один, в итоге для BER имеем p = P/3.

5.3Некогерентные системы

Внекогерентной СПИ могут использоваться лишь АМ или ЧМ, поэтому в такой системе невыгодно применять многопозиционные методы передачи. В связи с неопределенностью начальной фазы ожидаемого импульса во время приема не имеет смысла понятие разностного сигнала. Оптимальным способом предварительной обработки сигнала с белым шумом и в этом случае является корреляционный прием, но необходимо использовать два (для АМ) или четыре (для ЧМ) параллельно включенных приемника. Каждая пара приемников настроена на прием двух квадратурных составляющих импульса определенного вида, поэтому в ней используются опорные колебания соответствующей несущей частоты, но сдвинутые по фазе на 90° (напомним, что при АМ лишь один из двух символов является импульсом, а второй – это пауза, поэтому нужна лишь одна пара приемников).

125

Рис. 5.4. Функциональная схема демодулятора некогерентного сигнала с ЧМ

На рис. 5.4 приведена функциональная схема демодулятора некогерентного сигнала с ЧМ, причем фазовые детекторы играют роль перемножителей высокочастотного входного сигнала и гармонического опорного колебания, а RC-цепь с постоянной времени, намного превышающей длительность импульса входного сигнала, выполняет функции интегратора (см. формулу (2.27)). Компаратор выносит решение “передан символ 0”, если в момент окончания импульса напряжение на выходе верхнего сумматора оказалось больше, чем на выходе нижнего.

Обратите внимание, что на схеме нужно было бы показать цепи, по которым подаются тактовые импульсы, задающие моменты срабатывания компаратора и осуществляющие обнуление интегрирующей цепочки непосредственно перед началом каждого импульса.

Вероятность ошибки при демодуляции двоичного импульса (BER) минимальна при заданной величине qc, когда передается один из двух ортогональных сигналов равных энергий, например, с ЧМ, и определяется формулой

Видно, что и в некогерентной СПИ вероятность ошибки определяется величиной энергии принимаемого импульса по отношению к спектральной плотности шума. Эта зависимость также представлена на рис. 5.2, чтобы можно было сравнить качество передачи сигнала в когерентной и некогерентной системах при прочих равных условиях.

Как и следовало ожидать (см. разд. 5.1), BER в когерентной системе всегда меньше чем в некогерентной. При приеме сильного сигнала (величина BER мала, нижняя штриховая прямая на рис. 5.2), чтобы в некогерентной си-

126

стеме обеспечить то же значение BER, которое достигается в когерентной СПИ, нужно лишь немного увеличить мощность передатчика – на единицы и даже доли децибела (напомним, что в децибелах по формуле 10∙lg(E1/E2) выражается отношение энергий или мощностей двух сигналов). При приеме очень слабого сигнала это отношение возрастает до единиц и десятков децибел, то есть именно в этих условиях преимущество когерентной СПИ особенно ощутимо. Отметим, кстати, что в нормальных условиях функционирования СПИ величина qc обычно превышает 10–15 дБ.

5.4Частично-когерентные системы

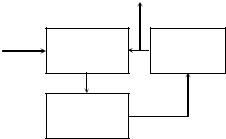
Вчастично-когерентной системе оптимальный демодулятор должен выполнять те же операции (5.3) и (5.4), но текущая фаза генератора опорного колебания w(t) подстраивается под изменения этого параметра в принимаемом сигнале при помощи системы ФАПЧ. Схема такого генератора для СПИ

сАМ или ЧМ представлена на рис. 5.5, где обозначено: ФД – фазовый детектор; ФНЧ – фильтр нижних частот; ГУН – генератор, управляемый напряжением. Это простейшая система автоматического регулирования. В

w(t)

u(t)

ФНЧ

Рис. 5.5. Генератор опорного колебания с петлей ФАПЧ

ней при рассогласовании фазы генератора относительно входного сигнала в ту или другую сторону на выходе ФД появляется напряжение соответствующего знака. Оно воздействует на частоту и, следовательно, фазу генератора. Фильтр НЧ, у которого частота среза во много раз меньше частоты повторения импульсов, служит для сглаживания флуктуаций управляющего напряжения, обусловленных шумом.

Если в СПИ для каждого из возможных сигналов имеется противоположный сигнал (однократная или многократная ФМ либо ОФМ, КАМ), такой генератор работать не будет, так как в процессе фильтрации в ФНЧ эти сигналы, появляясь в среднем одинаково часто, практически уничтожают друг друга (в спектре каждого из таких сигналов отсутствует составляющая несущей частоты).

По этой причине в частично-когерентной системе перечисленные методы модуляции применяются лишь в относительной форме. Это позволяет

128

(5.4), определяется формулой (5.13). Ошибка на втором этапе (рис. 5.7) произойдет в одном из двух случаев:

1)на первом этапе при демодуляции первого из двух импульсов произошла ошибка, второй импульс принят правильно;

2)первый импульс принят правильно, второй – с ошибкой.

В итоге битовая вероятность ошибки при демодуляции сигнала с ОФМ

равна

то есть BER в частичнокогерентной СПИ с ОФМ всего лишь в два раза больше чем BER в идеальной, когерентной СПИ с ФМ. Этим объясняется столь широкое использование ОФМ и когерентного метода приема таких сигналов.

Существует также некогерентный метод демодуляции сигнала с ОФМ. Для реализации этого метода на фазовый детектор приемника, рассчитанного на демодуляцию ФМ-сигналов и, следовательно, работающего в соответствии с (5.3) и (5.4), подается в качестве опорного колебания w(t) предыдущий принятый радиоимпульс. Его можно получить с выхода линии задержки.

Битовую вероятность ошибки можно вычислить по формуле (5.18), но величину qc2 следует удвоить, так как решение выносится после приема составного сигнала, содержащего два импульса. Здесь величина BER больше, чем при использовании когерентного метода приема, так как опорное колебание кроме составляющей, когерентной с полезным принимаемым сигналом, содержит также шумовую составляющую. Эта разница тем больше, чем меньше отношение сигнал/шум.

При использовании многопозиционных методов модуляции, кроме АМ и ЧМ, необходимо проводить ФАПЧ опорного генератора на гармониках несущей частоты более высокого порядка. Так, в СПИ с двукратной ФМ или

сКАМ генератор подстраивается по четвертой гармонике, а для трехкратной ФМ нужно перейти на восьмую гармонику.

Взаключение отметим интересную особенность СПИ, использующих относительные методы манипуляции в любой форме. Это – парное группирование ошибок, то есть при увеличении отношения сигнал/шум возрастает относительная доля ошибок, поражающих два соседних символа, по сравнению

содиночными ошибками. Это свойство нужно учитывать при выборе корректирующего кода. Например, код с проверкой на четность не будет замечать такие ошибки, если внутри кодовой комбинации окажутся оба символа пары, что весьма вероятно при использовании длинных комбинаций.

129

5.5 Прием сигнала в условиях многолучевости

Как видно из обсуждения, проведенного в разд. 5.1, реализация когерентной СПИ была бы возможна лишь при использовании канала передачи сигналов, идеального в том смысле, что его амплитудно-частотная и фазочастотная характеристики неизменны во времени и, следовательно, могут быть точно известны в пункте приема. Частично-когерентная и некогерентная СПИ также работают в условиях, почти идеальных, когда фазовый сдвиг в канале медленно меняется во времени одинаково на всех частотах. Обеспечить такие условия можно при передаче сигнала по кабельной линии либо при радиосвязи, когда радиотрасса проходит в однородной среде вдали от объектов, могущих вызвать отражение или рассеяние радиоволн, например, в линии спутниковой связи.

При распространении радиоволн в неоднородной тропосфере на расстояние всего лишь в десятки километров, над неровной земной или водной поверхностью и, тем более, в условиях города поле, падающее на приемную антенну, является суммой большого количества волн, часто называемых лучами. Эти волны обусловлены отражениями первичного поля от различных объектов (зданий, деревьев, автомобилей, холмов и т.п.), находящихся вблизи трассы. Разделить эти лучи и определить параметры каждого из них обычно не представляется возможным, поэтому полагают, что амплитуды и задержки (следовательно, и фазовые сдвиги) всех лучей случайны и даже взаимно независимы. Для полноты картины добавим, что обычно все эти параметры еще и случайным образом изменяются во времени. Такой канал назы-

вается каналом со случайно изменяющимися параметрами, а искажения сиг-

нала, передаваемого в таком канале, классифицируются как воздействие

мультипликативной помехи (см. разд. 1.5).

На рис. 5.8 в качестве примера приведена одна из реализаций случайно изменяющейся амплитуды принимаемого сигнала.

Даже если среднее значение амплитуды Ac достаточно велико, существуют такие случайно расположенные интервалы времени случайной длительности (помечены жирными линиями), когда амплитуда падает ниже уровня Aп, при котором еще возможен нормальный прием сигнала, то есть его демодуляция с заданной величиной BER. Можно считать, что при этом связь нарушается. Очевидно, что величина Aп определяется уровнем аддитивного шума на входе приемника.

130

A(t)

Aс

Рис. 5.8. Пример флуктуаций амплитуды принимаемого сигнала в канале с многолучевостью

Обычно полагают, что случайная амплитуда сигнала имеет релеевское распределение вероятности

где σ – среднеквадратическое значение флуктуаций каждой из квадратурных составляющих сигнала, при этом Aс=1,2533σ

(рис. 5.9). Вероятность того, что в заданный момент времени амплитуда сигнала окажется ниже порога Aп, определяется обычным образом

Тогда величину среднего суммарного времени нарушения связи на интервале Т можно определить как Tç TPç .

W(A)

Рис. 5.9. Релеевское распределение вероятности амплитуды сигнала

Конечно, уменьшить это время можно путем увеличения мощности передатчика, но существует более изящный и, можно сказать, более эффективный способ. Он называется разнесенным приемом и применяется как в аналоговых, так и в цифровых СПИ.

Для реализации N-кратного разнесенного приема, во-первых, организуют N параллельных каналов (ветвей разнесения) для одновременной передачи одного и того же сигнала и, во-вторых, применяют специальное устройство для того, чтобы из этих N принятых сигналов сформировать один сигнал, обладающий лучшими свойствами, нежели сигналы в ветвях разнесения.

Если флуктуации сигналов в ветвях разнесения полностью идентичны