
Расчет диэлектрических волноводов и объемных резонаторов
..pdf
101
отличными от размеров, которые он бы имел без учѐта краевого эффекта, и
эффективной диэлектрической проницаемостью эф . . Расчѐт геометрических
размеров резонатора производится в соответствии с методикой, изложенной в [5]. 1. Резонансная длина волны определяется выражением:
0 |
2 а эф |
r . эф |
|
2 а эф |
r . эф |
. |
(4.5.4) |
|
mn |
|
|
|
|||||
|
1 .841 |
|
|
|
||||
Из формулы (4.5.4) следует, что для определения резонансной длины |
||||||||
волны необходимо знать r . эф . |
и а эф . . Однако, |
определить их непосредственным |
||||||
расчѐтом достаточно трудно. Поэтому, для расчѐта удобно использовать результаты расчѐтов изложенных в [5], которые позволяют определить радиус резонатора по заданным 0 , εr и h.
Для определения радиуса резонатора а используем табл.3.6 из [5]. В табл.3
приведены резонансные длины волн 0 [см] плоского круглого резонатора для
разных типов колебаний при εr=2,7, h=0,2 см.
Таблица 3 Резонансные длины волн
a/h |
E110 |
E110 |
E210 |
E210 |
|
|
|
|
|
2,5 |
1,63 |
3,32 |
1,98 |
1,42 |
|
|
|
|
|
5,0 |
3,03 |
6,18 |
3,67 |
2,64 |
|
|
|
|
|
7,5 |
4,41 |
9,00 |
5,36 |
3,85 |
|
|
|
|
|
10,0 |
5,77 |
11,8 |
7,03 |
5,06 |
|
|
|
|
|
12,5 |
7,14 |
14,6 |
8,21 |
6,28 |
|
|
|
|
|
15,0 |
8,50 |
17,14 |
10,4 |
7,49 |
|
|
|
|
|
Из неѐ находим, что резонансной длине волны 0 9 см при волне типа Е110

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
102 |
соответствует отношение |
a/h =7,5, откуда а 7 ,5 h 1,5 см. |
|
||||||||||||||||
|
По |
известному радиусу |
резонатора |
можно определить |
r . эф . и а эф . и |
|||||||||||||
проверить правильность определения 0 . |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. a эф |
a |
1 |
2 h |
|
a |
|
1,77 |
|
1, 45 |
а 1,73 |
см. |
(4.5.5) |
||||||
|
ln |
|
|
|
|
|||||||||||||
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
a |
|
|
2 h |
|
|
|
|
|
|
|
|
2. |
rэф |
|
|
C эф( ) |
, |
|
|
|
|
|
|
|
|
|
|
(4.5.6) |
||
|
(1 ) |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
C эф |
|
|
|
|
|
|
|
|
|
|
|
|
||
где |
C |
( ) |
|
C ( ) |
C |
( ) |
, |
C (1) |
C (1) |
C (1) , |
|
|
||||||
|
|
эф |
|
|
0 эф |
|
кэф |
|
|
эф |
|
0 эф |
кэф |
|
|
|||
C 0 эф
С к . эф
|
r |
а 2 |
|
J |
m 1 |
( ) J |
m 1 |
( |
|
|
) |
, |
C |
1 |
|
а 2 |
|
|
J |
|
( |
|
|
) J |
|
|
( |
|
) |
, ( 4.5.7) |
||||||||||||||
|
|
|
|
|
|
1 |
|
|
mn |
|
mn |
|
|
0 эф |
|
|
|
|
|
1 |
|
m 1 |
|
mn |
|
|
m 1 |
|
mn |
|
|
|||||||||||||
|
|
h |
|
|
|
|
J m2 ( mn ) |
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
J m2 ( mn ) |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
а |
120 Z |
w |
( 2 a , h ,1) |
|
2 |
r |
a |
, |
С к1 |
|
|
а |
|
120 |
|
|
|
|
2 a |
, |
|
|
|
(4.5.8) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
. эф |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
Z w ( 2 a , h , r ) |
|
|
h |
|
|
|
|
|
|
|
|
|
Z W ( 2 a , h ,1) |
|
h |
|
|
|
|
|
|||||||||||||||||||
|
|
1, п р и m 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
2 , п р и m 0 |
|
|
=> |
|
|
|
|
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
= |
120 |
|
|
2 а |
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
73 15 |
|
4 ,3 |
1 |
|
|
, |
|||||||||||
Z |
w |
( 2 а , h , |
r |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln( 17 ( а / |
2 h 0 ,92 ) |
|
|
|
|
|
3 ,78 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z w ( 2 а , h ,1) =ZW ( 2 а , h , r |
|
) |
|
|
|
|
|
|
=6,19 |
|
|
, |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
C |
1 |
|
= C |
|
|
|
|
1 |
|
|
12 ,36 |
|
10 |
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
0 эф |
0 эф |
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
C к . эф . |
|
1,5 |
|
|
120 6 ,19 |
|
|
|
|
|
2 2 ,7 1,5 |
|
|
27 10 |
2 , |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
0 , 2 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 ,78 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
C |
к1 . эф |
|
1,5 |
|
|
120 |
|
|
|
|
2 |
|
1,5 |
=10,3 10 |
2 , |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
2 |
|
|
|
|
6 ,19 |
|
|
|
0 , 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||

103
C эф( ) C
C эф(1) C
( |
) |
C |
( ) |
0 |
эф |
|
кэф |
(1) |
C |
(1) |
|
0 эф |
|
кэф |
|
=0,33+0,26=0,59,
= 0,123+0,1=0,223,
rэф |
|
C |
эф( ) |
= |
0 ,59 |
|
|
|
2 ,67 , |
а эф |
|
1,73 |
см. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
C |
(1 ) |
0 , 223 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
эф |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2 а |
|
|
r . эф |
|
|
|
|
2 а эф |
r . эф |
|
|
|
|
|
|
|
|
|||
0 |
|
эф |
|
|
|
|
= |
2 |
|
2 ,67 1,73 |
9 ,7 |
см. |
||||||||||
|
|
|
mn |
|
|
|
1,841 |
|
|
1,841 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Расчет показал достаточно хорошее совпадение заданной и расчетной длин волн.
Расчѐт добротности резонатора
Используем выражение для полной добротности резонатора Q пол
|
|
|
|
|
|
1 |
|
1 |
tg , |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Q п |
Q 0 |
||
|
|
|
|
|
|
|
|
|
||
где Q 0 |
|
Q |
м Q d |
, |
Q 0 - собственная добротность резонатора, |
|||||
Q м |
|
Q d |
||||||||
|
|
|
|
|
|
|
|
|
||
tg |
|
10 |
3 10 |
4 - тангенс угла потерь в диэлектрике. |
||||||
|
|
|
|
|
|
|
|
|
|
|
Полагая, что пластины резонатора выполнены из меди, имеющей проводимость
5 ,8 10 7 См/м |
, |
tg |
|
|
10 |
3 10 |
4 и |
|
0 |
|
4 |
10 |
7 , |
|
далее получаем: |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
1 / |
0 м |
|
|
|
1, 207 |
10 |
6 |
м, |
|
||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
|
h |
|
4 ,973 10 3 , |
|
|
|
|
|
Q |
|
|
|
1 |
|
909 . |
(4.5.9) |
||||
|
м |
|
|
|
|
|
|
|
d |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В результате Q п |
|
|
|
1 |
|
|
|
1 |
416 ,5 . |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
tg |
|
|
|
|
|
|
|
|
|
|||||||||
|
Q 0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
104
4.6 Расчет прямоугольного планарного резонатора
Исходные данные:
Тип резонатора: прямоугольный планарный диэлектрический. Тип колебаний:
E110, т.е. m=1, n=1, p=0. Рабочая частота f0= 3 ГГц. Толщина диэлектрика h =2мм.
Относительная диэлектрическая проницаемость εr =6, окружающая средавоздух.
Расчет структуры поля и параметров резонатора
1. Структура электромагнитного поля в резонаторе.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнения Максвелла, описывающие электромагнитное |
|
поле rot E j a H , |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
rot H |
|
j a E , можно преобразовать в инвариантную форму (см. (1.14)): |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 E |
|
|
|
j grad |
|
|
|
|
|
|
j |
|
grad |
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
(4.6.1а) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
E |
q |
|
a |
|
|
H |
q |
|
|
e |
3 |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
2 H |
|
|
|
j grad |
|
|
|
|
j |
|
grad |
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
(4.6.1б) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
H |
q |
a |
|
|
E |
q |
|
e |
3 |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||
где H |
e1 H q |
|
e 2 H q |
; E e1 E q |
e 2 |
E q |
|
; E е1 |
E q |
|
е 2 |
E q |
|
; |
|
|
|
|
grad |
e1 |
|
e 2 |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
q1 |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q 2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Так как в резонаторе отсутствует продольная составляющая магнитного |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
поля |
Н z и |
|
поле |
не |
|
|
распространяющееся |
|
( |
0 ), |
|
находим |
составляющие |
||||||||||||||||||||||||||||||||||||||||||
поперечного магнитного поля из уравнения (4.6.1б) :
|
|
|
|
|
|
|
|
|
|
|
|
|
grad |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 H |
|
|
j |
a |
|
|
E |
z |
k |
0 |
, |
|
|
|
|
(4.6.2) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
H |
i H x |
|
|
j H y |
, |
grad |
|
i |
|
j |
, |
||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
y |
|||||
Н |
|
|
|
j a |
|
Е z |
, |
|
Н |
|
|
j |
a |
|
Е z |
. |
|
|
||||||||||
x |
|
|
|
у |
|
|
|
|
|
|||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
2 |
|
|
х |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Они выражены через составляющую Еz, которую определим из волнового

|
|
|
|
|
|
|
|
|
105 |
|
уравнения |
2 E z |
|
2 E z |
2 E |
|
и |
его |
общего |
решения: |
|
х 2 |
у 2 |
z |
||||||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
Еz=(Acoskxx+Bsinkxx)(Ccoskyy+Dsinkyy).
|
|
Применив граничные условия Олинера: |
Е z |
0 при х=0, х=а |
и |
|
Е z |
0 |
||||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
y |
|
|
при у=0, у=b, получим выражение для Еz=Еz0coskxx coskyy, |
где |
2 |
k x2 |
k у2 , |
||||||||||
k x |
|
m |
, |
k y |
n |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||
|
|
a |
|
b |
|
|
|
|
|
|
|
|||
Используя (4.6.2) найдем выражения, определяющие структуру поля:
|
|
|
Еz=Еz0cos |
m |
|
x cos |
n |
|
y, |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
||||
|
|
|
Н x |
|
|
|
jH x 0 |
cos |
|
m |
|
|
x sin |
n |
|
y , |
||||||||||||||||
|
|
|
|
|
a |
|
|
|
b |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Н y |
|
|
|
jH |
|
|
|
sin |
|
m |
|
|
x cos |
|
|
n |
|
y , |
|||||||||||
|
|
|
y 0 |
|
|
|
a |
|
|
|
|
b |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где Нx0= Еz0 |
a k x |
|
. Ну0=Ez0 |
a k y |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3. Резонансная длина волны типа Еmn0 определяется выражением (3.2.21) |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
рез |
|
|
|
|
|
|
2 |
|
|
|
эф . |
|
|
|
|
|
|
|
, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
m |
2 |
|
|
|
|
|
n |
|
|
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
эф |
|
|
|
|
|
|
|
|
|
эф |
|
|
|
|
|
||||
где m - количество вариаций поля по оси X, |
|
|
n -количество вариаций поля по оси |
|||||||||||||||||||||||||||||
Z, r эф , а эф , в эф - |
эффективная относительная диэлектрическая проницаемость |
|||||||||||||||||||||||||||||||
диэлектрика и эффективные размеры пластины.

106
4. Эффективная диэлектрическая проницаемость эф находится по формуле
Сэф ,
эф С 1эф
где |
C |
- |
|
эффективная |
ѐмкость |
резонатора |
прямоугольного |
|
сечения |
с |
|||||
|
эф |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
диэлектрической относительной проницаемостью подложки диэлектрика r , |
|
|
|||||||||||||
|
C 1 |
- |
|
эффективная |
ѐмкость |
резонатора |
прямоугольного |
|
сечения |
с |
|||||
|
эф |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
диэлектрической относительной проницаемостью диэлектрика r =1. |
|
|
|
|
|
||||||||||
|
В общем случае эффективная ѐмкость равна C |
= С |
+2 |
С |
|
+ С |
|
. |
|||||||
|
|
|
|
|
|
|
|
эф |
0 эф |
|
|
k 1 эф |
|
k 2 эф |
|
Здесь |
С |
= |
r а в |
- эффективная ѐмкость плоского конденсатора, |
|
|
|
|
|
||||||
|
|
|
|
|
|
||||||||||
|
0 эф |
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Сk 1 эф
Сk 1 эф
, С k 2 эф - эффективные краевые ѐмкости, определяемые формулами:
|
в |
120 Z |
W |
( а , h ,1) |
|
|
r |
а |
, С k 2 эф |
|
а |
120 Z |
W |
( в , h ,1) |
|
|
r |
в |
||||
= |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
. |
|||||
2 |
Z W2 ( а , h , r ) |
|
h |
|
2 |
Z W2 ( в , h , r ) |
|
h |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Ёмкость C |
1 |
вычисляется по этим же формулам, но вместо |
r |
в них надо |
||||||||||||
|
эф |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
подставить 1; |
и |
|
- символы |
Кроникера, причем 1 при |
n=0, |
|
2 при |
|||||||||
n 0 ; 1 при |
m=0, |
|
2 при |
|
|
m 0 ; |
ZW ( а , h , r |
) - волновое сопротивлении |
||||||||
НПЛ, у которой а |
- |
ширина |
полоски; |
h, |
r - |
толщина |
и относительная |
|||||||||
диэлектрическая проницаемость подложки. |
|
|
|
|
|
|
|
|||||||||
При вычислении |
С |
Z |
W |
( в , h , |
r |
) |
- |
волновое сопротивлении |
НПЛ, у |
|||||||
|
|
|
|
k 2 эф |
|
|
|
|
|
|
|
|
|
|
||
которой в -ширина полоски, h, r - толщина и относительная диэлектрическая

107
проницаемость подложки. |
При отношении |
|
а |
2 : |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
ZW |
( а , h , r |
)= |
120 |
а |
|
2 |
|
|
|
|
,08 ( а / 2 h 0 ,92 |
|
1 |
, |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(ln( 17 |
) |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
r |
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
120 |
в |
|
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||||||||||
ZW |
( в , h , r |
)= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(ln( 17 |
,08 ( в / 2 h 0 ,92 ) . |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
r |
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Значения а эф и в эф , входящих в формулу, |
определяющую рез , равны: |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
120 |
а |
3 |
h |
|
|
|
|
4 |
|
120 |
в |
3 |
h |
|
|
4 |
||||||||||||||||||||||
а эф |
|
|
|
|
|
|
, в |
эф |
|
|
|
|
. |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( в , h , r ) |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
Z W ( а , h , r ) |
|
|
|
|
эф . |
|
Z W |
|
|
|
эф . |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Пример расчѐта:
Как и в случае круглого планарного резонатора, для оценки резонансной
длины волны 0 при заданном отношении |
а |
, r и h, рекомендуем |
|
||
|
в |
|
воспользоваться табл.3.4 из [5]. В табл.3.4 резонансные длины волны 0 даны для
колебаний Е110 |
и Е100 |
при различных в , |
а |
и r . |
|
|
|
в |
|
|
|||||
|
|
|
|
|
|
||
Для нахождения резонансной длины волны 0 возьмѐм отношение |
а |
=1. |
|||||
в |
|||||||
|
|
|
|
|
|
||
Тогда для подложки из ФАФ-4 ( r 2 ,3 ) при в 4 см оценка резонансной длины волны колебания Е110 согласно [5] дает 0 =9,142 см.
Расчетное значение рез получим, подставляя численные значения а , r , h,
в
в выше приведенные соотношения. В результате получим:
108
|
|
|
|
|
|
120 |
|
а |
|
2 |
|
|
|
|
|
1 |
|||||||
1. Z ( а , h , |
|
)= |
|
|
|
|
|
|
|
|
|
|
|
|
(ln( 17 ( а |
/ 2 h |
0 ,92 ) |
|
= |
||||
r |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
120 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
10 ,7 Ом. |
||
|
|
|
20 |
|
|
|
|
(ln( 17 |
,08 (10 0 ,92 |
) |
|
3 , 43 |
|||||||||||
|
|
|
|||||||||||||||||||||
|
1,51 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2. |
ZW ( а , h ,1 )= ZW ( а , h , r |
|
|
|
)=5,15 |
Ом. |
|
|
|
|
|
|||||||||||||||||||||
) r |
|
|
|
|
|
|||||||||||||||||||||||||||
3. |
ZW ( в , h , r )= 3, 43 Ом. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
4. |
ZW ( в , h ,1 )= ZW ( а , h , r |
|
|
|
=5,15 |
Ом. |
|
|
|
|
|
|||||||||||||||||||||
) r |
|
|
|
|
|
|||||||||||||||||||||||||||
5. |
С |
|
= |
|
r |
|
а в |
|
= |
2 .3 16 10 |
4 |
|
0 , 46 . |
|
|
|
|
|
|
|||||||||||||
0 эф |
h |
4 0 , 2 10 |
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
6. |
С |
1 |
= |
|
|
а в |
|
|
=0,2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
0 эф |
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
7. |
|
|
= |
|
в |
|
120 |
|
Z W ( а , h ,1) |
|
r а |
120 |
|
5 ,15 |
|
|
6 ,52 . |
|||||||||||||||
С k 1 эф |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
46 |
||||||||
2 |
|
|
|
|
2 |
( а , h , r ) |
|
h |
3 , 43 2 2 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Z W |
|
|
|
|
|
|
|
||||||||||||||||
8. |
С |
= С |
|
|
=6,52. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
k 2 эф |
|
|
|
|
k 1 эф |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
9. |
1 |
= |
|
в |
|
|
|
120 |
|
|
а |
120 |
|
|
|
|
3 ,5 . |
|
|
|
||||||||||||
С k 1 эф |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
||||||||
2 |
|
|
|
|
|
|
|
|
5 ,15 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
Z W ( а , h ,1) |
|
h |
|
|
|
|
|
|
|
|
|
||||||||||||||||
10. С k1 2 эф =3,5.
11. C |
|
= С |
|
+2 С |
|
+2 С |
|
=0,46+4 6 ,52 26 ,54 . |
|||
|
эф |
|
|
0 эф |
|
|
k 1 эф |
|
k 2 эф |
|
|
12. C |
1 |
= С |
1 |
+2 С |
1 |
|
+2 С |
1 |
=0,2+4 3,5 14 , 2 . |
||
|
эф |
|
|
0 эф |
|
|
k 1 эф |
|
k 2 эф |
|
|
13. эф |
|
С эф |
= |
26 ,54 |
|
1,87 . |
|
||||
С эф1 |
|
|
|
||||||||
|
|
|
14 , 2 |
|
|
|
|
||||
109
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
120 |
4 3 |
|
0 , 2 |
|
|
|
||||||||||
14. |
|
|
|
|
|
|
|
120 а 3 h |
|
|
|
|
4 |
|
|
|
|
4 |
|
4 ,7 см. |
||||||||||||||||
а эф . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
( а , h , |
|
) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
3 , 43 |
2 ,3 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
W |
|
|
|
|
|
r |
|
|
эф . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
15. |
в эф =4,7 см. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
16. |
рез |
|
|
|
|
|
|
|
|
2 |
|
эф |
|
|
|
|
|
|
|
|
|
|
= |
2 1,37 |
4 ,7 |
|
9 ,13 |
см. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
1, 41 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
m |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
эф |
|
|
|
|
|
|
|
эф |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Вывод: |
|
результаты расчѐта |
рез дают хорошее совпадение с оценочным |
||||||||||||||||||||||||||||||||
значением 0 .
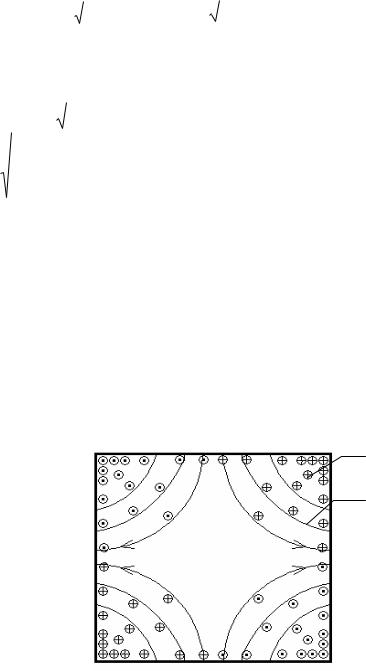
Добротность планарного прямоугольного резонатора рассчитывается аналогично приведенному расчету в п.4.5. Структура поля показана на рис.31.
H
E
Рис.31 Структура поля колебания Е110.
110
Литература
1.Вольман В.И., Пименов Ю. В. Техническая электродинамика. - М.: Связь,
1971. -486 с.
2.Федоров Н.Н. Основы электродинамики. – М.: Высшая школа, 1980. - 399 с.
3. Никольский В.В., Никольская Т.И. Электродинамика и |
распространение |
радиоволн. – М.: Наука, 1989. - 540 с.
4.Взятышев В.Ф. Диэлектрические волноводы.–М.: Советское радио, 1970.-216 с.
5.Справочник по расчѐту и конструированию СВЧ полосковых устройств. Под редакцией Вольмана В.И.. - М.: Радио и связь, 1982. - 328 с.
6.Ярив А., Юх П. Оптические волны в кристаллах. - М.: Мир, 1987. - 616 с.
7.Гончаренко А.М. Редько В.П. Введение в интегральную оптику. - Минск:
Наука и техника, 1975. - 147 с.
8.Гончаренко А. М., Карпенко В. А.Основы теории оптических волноводов. -
М.: Едиториал УРСС, 2004. - 236 с.
9.Петров Б.М. Электродинамика и распространение радиоволн.- М.: Горячая линияТелеком, 2007.-558 с.
10.Пименов Ю.В., Вольман В.И., Муравцов А.Д. Техническая электродинамика:
Учебное пособие для вузов. - М.: Радио и связь, 2002. - 536 с.
11.Гильденбург В.Б., Миллер М.А. Сборник задач по электродинамике: Учебное пособие для вузов. - М.: Физматлит, 2001. - 164 с.
12.Чернышев А.А. Кирпиченко Л. И. Работы студенческие учебные и выпускные
