Основы программирования

и минусы. Первый – построчное считывание результатов выполнения команды с помощью объекта класса SQLiteDataReader. Реализация этого подхода требует большее, по сравнению со вторым, количество программного кода, однако дает разработчику несравнимо более богатый набор возможностей для контроля над процессом считывания и обработки данных из результата выполнения SQL-запроса.

Для определения имеется ли в базе данных пользователь с определенным логином и паролем созданим метод аналогичный методу UsersCount:

public bool ValidUser(string username, string password)

{

SQLiteConnection conn = new SQLiteConnection(dataSource); try

{

conn.Open();

if (conn.State == ConnectionState.Open)

{

SQLiteCommand cmd = conn.CreateCommand(); cmd.CommandText = string.Format("SELECT login, password, role"

+"FROM users"

+"where login = '{0}' AND"

+"password = '{1}'", username, password);

var usersCount = (int)cmd.ExecuteScalar(); return usersCount > 0;

}

}

catch

{

return false;

}

finally

{

conn.Dispose();

}

return false;

}

31

ГЛАВА 5

ТЕСТИРОВАНИЕ ПРИЛОЖЕНИЯ

Тестирование программного обеспечения – это проверка соответствия между реальным и ожидаемым поведением программы, осуществляемая на конечном наборе контрольных примеров. Количество и сами контрольные примеры определяются тестировщиков исходя из его знаний и квалификации [4, 5]. Контрольный пример – это совокупность предварительных условий, входов (включая действия, где это применимо) и ожидаемых результатов, разработанных для управления выполнением элемента тестирования для достижения целей тестирования, включая корректную реализацию, идентификацию ошибок, проверку качества и получение другой значимой информации.

Существуют различные подходы и разновидности тестирования:

–функциональное тестирование;

–тестирование пользовательского интерфейса;

–тестирование безопасности;

–тестирование взаимодействия;

–нагрузочное тестирование;

–стрессовое тестирование;

–тестирование стабильности;

–объемное тестирование;

–тестирование установки;

–тестирование удобства пользования;

–тестирование на отказ и восстановление;

–конфигурационное тестирование;

–дымовое тестирование;

–регрессионное тестирование;

–повторное тестирование;

–тестирование сборки;

–санитарное тестирование.

В рамках курсовой работы необходимо провести функциональное тестирование, путем написания автоматических тестов и ручного тестирование пользовательского интерфейса. Для написания автоматических тестов в зависимости от используемых технологий существуют готовые библиотеки, которые позволяют ускорить и автоматизировать процесс тестирования функционала разрабатываемого приложения. Для .Net Framework популярна библиотека NUnit, чтобы добавить автоматические тесты к вашему приложению создайте новый проект в вашем решении (рис. 29) из шаблона «Тестовый проект

NUnit» (рис. 30).

32

Для того чтобы в новом проекте была возможность обращаться к классам тестируемого проекта, необходимо добавить на него ссылку (рис. 31, 32) и в файле теста добавить строку подключения зависимости «using BasicsOfProgramming», после этого можно приступать к непосредственному написанию автоматических тестов.

Рис. 31. Добавление ссылок в проект

Рис. 32. Поиск проекта в диспетчере ссылок

Добавим несколько простых тестов на методы класса Calculator:

[Test]

public void TestCalculatorGetAdd()

{

var calculator = new Calculator(4, 3); Assert.AreEqual(7, calculator.GetAdd());

}

[Test]

public void TestCalculatorGetDiv()

{

var calculator = new Calculator(6, 4); Assert.AreEqual(1.5, calculator.GetDiv());

}

34

[Test]

public void TestCalculatorGetMult()

{

var calculator = new Calculator(4, 3); Assert.AreEqual(12, calculator.GetMult());

}

[Test]

public void TestCalculatorGetSub()

{

var calculator = new Calculator(4, 3); Assert.AreEqual(1, calculator.GetSub());

}

В приведенном коде, используется класс Assert, он содержит методы для написания различного рода тестов. В приведенном примере используется метод AreEqual, который принимает два операнда на входе и проверяет что переданные операнды одинаковы. Для того чтобы запустить написанные тесты в меню «Тест» выберите «Выполнить все тесты» (рис. 33).

Рис. 33. Запуск тестов

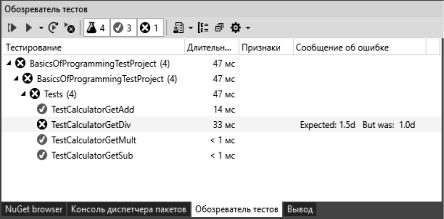
После запуска тестов откроется оснастка «Обозреватель тестов» (рис. 34). Как видно из рис. 34 один из тестов «провалился», в результате выполнения теста TestCalculatorGetDiv мы ожидали, поделив 6 на 4, получить значение 1,5, а в результате вызова метода calculator.GetDiv() было получено значение 1,0, следовательно необходимо провести отладку этого метода чтобы все тесты связанные с ним проходили. Представленная ошибка возникла из-за округления целочисленного операнда при делении, для решения этой про-

блемы достаточно сделать приведение типов к double:

public double GetDiv()

{

35

double firstDouble = Convert.ToDouble(firstNumber); double secondDouble = Convert.ToDouble(secondNumber); return firstDouble / secondDouble;

}

Рис. 34. Оснастка «Обозреватель тестов»

Аналогичным способом необходимо покрыть тестами все методы разработанных классов.

Основными целями ручного тестирование интерфейса являются выявления ошибок функциональности, необработанных исключений, несоответствия проектной документации. Для того чтобы провести ручное тестирование интерфейса необходимо составить тест планы в виде сценариев работы пользователя на естественном языке, пример тест плана на естественном языке представлен ниже:

1.Пользователь не заполняет поле «Логин».

2.Пользователь заполняет поле «Пароль».

3.Пользователь заполняет поле «Подтвердите пароль» аналогично полю «Пароль».

4.Пользователь нажимает кнопку «Зарегистрировать».

5.Пользователю отображается информационное окно о том, что необходимо заполнить поле «Логин».

После составления тест планов для покрытия всей функциональности разрабатываемого приложения необходимо по каждому тест плану провести тестирование с предоставлением результатов в виде скриншотов и заключения

оего выполнении или невыполнении. После выявления провалов тест планов, необходимо произвести отладку и снова выполнить тестирование, до тех пор, пока все тест планы не будут выполнены.

36

Глава 6

ВАРИАНТЫ ЗАДАНИЙ НА КУРСОВУЮ РАБОТУ

1. Шифр Гронсфельда

Этот шифр сложной замены, называемый шифром Гронсфельда, представляет собой модификацию шифра Цезаря числовым ключом. Для этого под буквами исходного сообщения записывают цифры числового ключа. Если ключ короче сообщения, то его запись циклически повторяют. Шифртекст получают примерно, как в шифре Цезаря, но отсчитывают по алфавиту не третью букву (как это делается в шифре Цезаря), а выбирают ту букву, которая смещена по алфавиту на соответствующую цифру ключа. Например, применяя в качестве ключа группу из четырех начальных цифр числа e(основания натуральных логарифмов), а именно 2718, получаем для исходного сообщения ВОСТОЧНЫЙ ЭКСПРЕСС шифртекст представленный в табл. 3.

Т а б л и ц а 3

Чтобы зашифровать первую букву сообщения В, используя первую цифру ключа 2, нужно отсчитать вторую по порядку букву от В в алфавите. Получается первая буква шифртекста Д.

2. Шифрование квадратом Полибия

В Древней Греции (II в. до н.э.) был известен шифр, называемый «квадрат Полибия». Шифровальная таблица представляла собой квадрат с пятью столбцами и пятью строками, которые нумеровались цифрами от 1 до 5. В каждую клетку такого квадрата записывалась одна буква. В результате каждой букве соответствовала пара чисел, и шифрование сводилось к замене буквы парой чисел. Для латинского алфавита квадрат Полибия имеет вид, представленный в табл. 4.

37

3. Шифр Хилла

Шифр Хилла является полиграммным шифром, который может использовать большие блоки с помощью линейной алгебры. Каждой букве алфавита сопоставляется число по модулю 26. Для латинского алфавита часто используется простейшая схема: A = 0, B = 1, …, Z = 25, но это не является существенным свойством шифра. Блок из n букв рассматривается как n-мерный вектор и умножается по модулю 26 на матрицу размера n × n.

4. Шифр Атбаш

Атбаш – простой шифр подстановки для алфавитного письма. Правило шифрования состоит в замене i-й буквы алфавита буквой с номером n–i+1, где n – число букв в алфавите.

5. Шифр Вижинера(для латинского алфавита)

Шифр Виженера – метод полиалфавитного шифрования буквенного текста с использованием ключевого слова. Шифр Виженера «размывает» характеристики частот появления символов в тексте, но некоторые особенности появления символов в тексте остаются. Главный недостаток шифра Виженера состоит в том, что его ключ повторяется. Шифр Виженера состоит из последовательности нескольких шифров Цезаря с различными значениями сдвига. Для зашифровывания необходимо использовать таблицу для латинского алфавита.

6. Шифр Вижинера(для кириллицы)

Для зашифровывания необходимо использовать таблицу с кириллицей.

7. Шифр Плейфера

Шифр Плейфера использует матрицу 5×5 (для латинского алфавита, для кириллического алфавита необходимо увеличить размер матрицы до 4×8), содержащую ключевое слово или фразу. Для создания матрицы и использования шифра достаточно запомнить ключевое слово и четыре простых правила. Чтобы составить ключевую матрицу, в первую очередь нужно заполнить пустые ячейки матрицы буквами ключевого слова (не записывая повторяющиеся символы), потом заполнить оставшиеся ячейки матрицы символами алфавита, не встречающимися в ключевом слове, по порядку (в английских текстах обычно опускается символ «Q», чтобы уменьшить алфавит, в других версиях «I» и «J» объединяются в одну ячейку). Ключевое слово может быть записано в верхней строке матрицы слева направо, либо по спирали из левого верхнего угла к центру. Ключевое слово, дополненное алфавитом, составляет матрицу 5×5 и является ключом шифра.

8. Шифр Скитала

Для шифрования сообщения использовались пергаментная лента и палочка цилиндрической формы с фиксированными длиной и диаметром. Пергаментная лента наматывалась на палочку так, чтобы не было ни просветов, ни нахлестов. Написание сообщения производилось по намотанной пергаментной ленте по длинной стороне цилиндра. После того, как достигался конец намотанной ленты, палочка поворачивалась на часть оборота и написание со-

38

общения продолжалось. После разматывания ленты на ней оказывалось зашифрованное сообщение. Расшифрование выполнялась с использованием палочки таких же типоразмеров.

9. Простая табличная перестановка

Можно записать сообщение в прямоугольную таблицу по маршруту: по горизонтали, начиная с верхнего левого угла, поочередно слева направо. Сообщение будем списывать по маршруту: по вертикалям, начиная с верхнего правого угла, поочередно сверху вниз. Полученная строка и есть зашифрованный текст.

10. Двойная табличная перестановка

Аналогично простой табличной перестановки для обеспечения дополнительной скрытности можно повторно зашифровать сообщение, которое уже прошло шифрование. Такой метод шифрования называется двойной перестановкой. В случае двойной перестановки столбцов и строк таблицы перестановки определяются отдельно для столбцов и отдельно для строк. Сначала в таблицу записывается текст сообщения, а потом поочередно переставляются столбцы, а затем строки. При расшифровании порядок перестановок должен быть обратным.

Для вариантов 1–10 Разработать программу, которая зашифрует введенный с клавиатуры текст и сохранит его в файл и базу данных и при необходимости считает зашифрованный текст из файла или базы данных и расшифрует данный текст.

11. Магический квадрат

Магическим квадратом порядка N называется квадратная таблица размера NxN, составленная из чисел 1, 2, … N2 так, что суммы по каждому столбцу, каждой строке и каждой из двух диагоналей равны между собой. Составить программу построит магический квадрат для заданного N, введенного с клавиатуры, сохранит его в виде изображения в файл.

12. Сложение и вычитание дробей с помощью метода «бабочка»

39

13. Решето Эратосфена

Решето Эратосфена – алгоритм нахождения всех простых чисел до некоторого целого числа n, который приписывают древнегреческому математику Эратосфену Киренскому. Решето подразумевает фильтрацию, в данном случае фильтрацию всех чисел за исключением простых. По мере прохождения списка нужные числа остаются, а ненужные исключаются.

14. Решето Сундарама

Решето Сундарама – детерминированный алгоритм нахождения всех простых чисел до некоторого целого числа n. Разработан индийским студентом Сундарамом в 1934 году.

15. Решето Аткина

Решето Аткина – алгоритм нахождения всех простых чисел до заданного целого числа N. Алгоритм был создан А.О. Аткином и Д.Ю. Бернштайном. Заявленная авторами асимптотическая скорость работы алгоритма соответствует скорости лучших ранее известных алгоритмов просеивания, но в сравнении с ними решето Аткина требует меньше памяти.

Для вариантов 13–15 разработать программу, позволяющую пользователю с клавиатуры ввести натуральное число N, от 1 до 50 и получить N – первых натуральных чисел. Составленное решето должно быть сохранено в виде изображения в файл.

16. Алгоритм ближайшего соседа в задаче коммивояжера

Коммивояжер желает посетить ряд городов и вернуться в исходный город, минимизируя суммарную длину переездов. Эта задача в математической форме формулируется как задача нахождения во взвешенном графе гамильтонова цикла минимальной длины и называется задачей коммивояжера. Алгоритм ближайшего соседа – один из простейших эвристических алгоритмов решения задачи коммивояжера. Относится к категории «жадных» алгоритмов. Формулируется следующим образом: пункты обхода плана последовательно включаются в маршрут, причем каждый очередной включаемый пункт должен быть ближайшим к последнему выбранному пункту среди всех остальных, еще не включенных в состав маршрута.

17. Метод ветвей и границ в задаче коммивояжера

Для решения задачи коммивояжера методом ветвей и границ необходимо выполнить следующий алгоритм:

Построение матрицы с исходными данными.

Нахождение минимума по строкам.

Редукция строк.

Нахождение минимума по столбцам.

Редукция столбцов.

Вычисление оценок нулевых клеток.

Редукция матрицы.

40