Оптические цифровые телекоммуникационные системы. Сборник задач с формулами и решениями

неравномерного квантования с сегментированной характеристикой компрессии А-типа, рекомендуемой МСЭ.

Рисунок 1.15 – Зависимость Aпз.кв. = ƒ(pс)

при неравномерном квантовании для гармонического сигнала

Решение

По зависимости Aз.кв = ƒ(Pс) (рисунок 1.15) видно, что допустимый диапазон изменения уровня гармонического сигнала, в котором защищённость от шумов квантования остаётся не ниже 27 дБ, при использовании неравномерного квантования с сегментированной характеристикой компрессии А-87,6/13 со-

ставляет 3дБ – (–43,86дБ) = 46,86 дБ ≈47 дБ.

Пилообразный вид зависимости объясняется следующим образом: начало графика — наклонная прямая — соответствует 0-му и 1-му сегменту характеристики компрессии А-87,6/13. Это зона равномерного квантования, поэтому помехозащищённость возрастает пропорционально возрастанию уровня сигнала(см. рисунок 1.14). При переходе ко 2-му сегменту помехозащищённость скачком уменьшается на 6 дБ, поскольку во 2-м сегменте величина шага квантования в 2 раза больше. Такая же картина повторяется при переходе к каждому последующему сегменту. Это зона неравномерного квантования. При достижении верхней

21

границы — 7 сегмента (Uогр) — наступает зона перегрузки, где защищённость сигнала резко падает, но уже за счёт шумов ограничения сигнала.

Задача 7

Обосновать, почему в ЦСП с ИКМ, предназначенной для передачи телефонных сигналов, следует применять неравномерное квантование с характеристикой компрессии, близкой к логарифмической.

Решение

В ЦСП с ИКМ, предназначенной для передачи телефонных сигналов, следует применять неравномерное квантование, так как при этом для слабых сигналов мощность шумов квантования Pш.кв уменьшается, а для сильных возрастает, что приводит к увеличению помехозащищённости Аз.кв для слабых сигналов и снижению Аз.кв для сильных, которые имели большой запас по помехозащищённости. В результате удаётся снизить разрядность кода (до 8), обеспечив при этом выполнение требований к помехозащищённости от шумов квантования в широком динамическом диапазоне сигнала, составляющем около 40 дБ. Таким образом происходит выравнивание Аз.кв в широком диапазоне изменения уровней сигнала. Эффект неравномерного квантования пропорционален сжатию динамического диапазона сигнала, которое осуществляется с помощью компрессора, обладающего нелинейной амплитудной характеристикой, близкой к логарифмической. В современных ЦСП находят применение две квазилогарифмические характеристики компандирования (типа Аи μ).

1.3Задачи для самостоятельного решения

1.1.Рассчитать и сравнить мощность шумов квантования при равномерном квантовании для заданных значений разряд-

ности кода m и напряжения ограничения Uогр (при использовании натурального симметричного кода).

1.2. Рассчитать и сравнитьвеличинышагов квантования для кодеров указанноготипапри заданномнапряжении ограниченияUогр.

22

1.3.На выходе линейного кодера в процессе кодирования отсчетов натуральным симметричным кодом некоторого канального сигнала были последовательно сформированы заданные кодовые комбинации. Определить сигнал на входе кодера и на выходе декодера, если в процессе передачи произошли ошибки

всимволах, помеченных в задании.

1.4.Задан отсчет сигнала и напряжение ограничения кодера. Записать кодовые комбинации, соответствующие данному отсчету, при использовании натурального симметричного и несимметричного кода.

1.5.Задана кодовая комбинация на выходе кодера аппаратуры ИКМ-30. Рассчитать амплитуду отсчета на входе кодера, а также номера сегмента и шага внутри сегмента характеристики компандирования, соответствующие данному отсчету, полагая,

что напряжение ограничения кодера равно Uогр.

1.6. На рисунке изображен спектр сигнала. Найдите минимальную частоту дискретизации, позволяющую избежать наложения. Предположите, что сигнал дискретизуется с частотой 16 кГц, и изобразите спектр дискретного сигнала в диапазоне ±16 кГц.

Частота, кГц

Спектр сигнала

1.7. Выбрать частоту дискретизации Fд первичного сигнала,

спектр которого ограничен частотами fн = 12 кГц и fв = 24 кГц. Для выбранной частоты дискретизации рассчитать и построить спектральную диаграмму АИМ-сигнала.

1.8.Запишите уравнение, выражающее теорему о полосовой дискретизации. Объясните, почему теорема о полосовой дискретизации представляет интерес для цифровой связи.

1.9.Выполнить операции равномерного квантования с ша-

гом δ = 0,6 и кодирования в восьмиразрядном симметричном ко-

23

де двух отсчетов аналогового сигнала с амплитудами U1 = 6,4 В и U2 = –18,6 В. Определить величины ошибки квантования. Изобразить полученные в результате кодирования кодовые комбинации в виде последовательности токовых и бестоковых посылок.

1.10.Выполнить операции равномерного квантования с шагом δ = 0,3 и кодирования в восьмиразрядном симметричном коде двух отсчетов аналогового сигнала с амплитудами U1 = 6,1 В

иU2 = 19,8 В. Определить величины ошибки квантования. Изобразить полученные в результате кодирования кодовые комбинации в виде последовательности токовых и бестоковых посылок.

1.11.Выполнить операции равномерного квантования с ша-

гом δ = 0,4 и кодирования в восьмиразрядном симметричном коде двух отсчетов аналогового сигнала с амплитудами U1 = 6,2 В и U2 = –18,6 В. Определить величины ошибки квантования. Изобразить полученные в результате кодирования кодовые комбинации в видепоследовательности токовых и бестоковых посылок.

1.12.Найдите минимальную теоретическую частоту дискретизации Fs, позволяющую избежать наложения, для полосового сигнала счастотными компонентами в диапазоне10МГц <f <20МГц.

1.13.Найдите минимальную теоретическую частоту дискрети-

зации Fs , позволяющую избежать наложения, для полосового сиг-

наласчастотнымикомпонентамивдиапазоне15МГц <f<29МГц. 1.14. Выбрать частоту дискретизации Fд первичного сигнала,

спектр которого ограничен частотами fн = 15 кГц и fв = 30 кГц. Для выбранной частоты дискретизации рассчитать и построить спектральную диаграмму АИМ-сигнала.

1.15. Выбрать частоту дискретизации Fд первичного сигнала,

спектр которого ограничен частотами fн = 5 кГц и fв = 10 кГц. Для выбранной частоты дискретизации рассчитать и построить спектральную диаграмму АИМ-сигнала.

1.16. Выполнить операции равномерного квантования с шагом δ = 0,7 и кодирования в восьмиразрядном симметричном коде двух отсчетов аналогового сигнала с амплитудами U1 = 6,2 В и U2 = 20 В. Определить величины ошибки квантования.

24

1.17.Выполнить операции равномерного квантования с шагом δ = 0,25 и кодирования в восьмиразрядном симметричном коде двух отсчетов аналогового сигнала с амплитудами U1 = 4 В и U2 = 20,6 В. Определить величины ошибки квантования. Изобразить полученные в результате кодирования кодовые комбинации в виде последовательности токовых и бестоковых посылок.

1.18.Выполнить операции равномерного квантования с ша-

гом δ = 0,3 и кодирования в восьмиразрядном симметричном коде двух отсчетов аналогового сигнала с амплитудами U1 = 9,3 В и U2 = 32 В. Определить величины ошибки квантования. Изобразить полученные в результате кодирования кодовые комбинации

ввиде последовательности токовых и бестоковых посылок.

1.19.Найдите минимальную теоретическую частоту дискрети-

зации Fs, позволяющую избежать наложения, для полосового сигналасчастотнымикомпонентамивдиапазоне20МГц <f<30МГц.

25

2 ПРЕОБРАЗОВАНИЕ СИГНАЛА

ВНЕЛИНЕЙНОМ КОДЕРЕ

СХАРАКТЕРИСТИКОЙ А-ТИПА

2.1Основные теоретические сведения

Численной характеристикой влияния шумов квантования на точность кодирования аналогового сигнала может служить отношение мощностей сигнала и шума квантования. Для двуполярного сигнала это отношение равно:

Для однополярного сигнала:

Pc 10,8 20lg( U ) 6n.,

Pш.кв Uогр

Изменение мощности передаваемого сигнала приводит к снижению величины сигнал–шум. На рисунке 2.1 приведена зависимость отношения сигнал–шум (с учетом искажений как квантования Pкв , так и ограничения Pогр ).

дБ

дБ

Рисунок 2.1 – Зависимость отношения сигнал–шум от уровня сигнала с нормальным законом распределения мгновенных значений

Резкое падение величины отношения сигнал-шум при превышении сигналом оптимального уровня вызвано ростом мощности искажений ограничения.

26

Уменьшение сигнала вызывает пропорциональное снижение отношения сигнал-шум, т. е. передача слабых сигналов сопровождается большими искажениями.

Если изменять шаг квантования пропорционально значению квантуемого сигнала, то отношение сигнал-шум при изменении сигнала будет сохраняться постоянным. Переменную величину шага можно получить, например, с помощью устройства с нелинейной амплитудной характеристикой и равномерного квантователя (рисунок 2.2).

Рисунок 2.2 – Структурная схема устройства неравномерного квантования

с компандированием аналогового сигнала

Исходный сигнал передается через устройство, коэффициент передачи которого обратно пропорционален величине сигнала, квантуется и проходит через схему, нелинейность которой обратная нелинейности входного устройства. Таким образом, перед квантованием осуществляется компрессия (сжатие) динамического диапазона входного сигнала, а после квантования — его расширение, что обеспечивает общую линейность системы передачи.

Совокупность операций сжатия диапазона, осуществляемого компрессором, и расширения, производимого экспандером, называется компандированием сигнала (рисунок 2.3).

Амплитудная характеристика входного устройства

Uвых = y(Uвх) (см. рисунок 2.3) называется характеристикой компрессии. Характеристика компрессии связывает шкалу равномерного квантования (ось ординат) со шкалой неравномерного квантования и характеризует любую систему неравномерного квантования даже при отсутствии компрессора как отдельного узла.

27

Рисунок 2.3 – Характеристика компрессии

Шаг неравномерногоквантования определяется из выражения

После разделения переменных и интегрирования получим

где с1 и с2 — постоянные интегрирования; μ ec2 . Функция y(Uвх) должна удовлетворять условиям:

ln(1 μ)

28

Подставляя b и с в выражение (2.3), получаем искомую за-

висимость y ln(1 μUвх ), широкоиспользуемую в АЦП ИКМ. ln(1 μ)

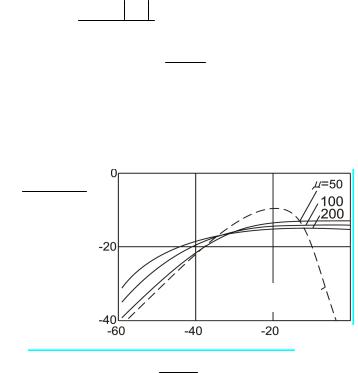
Зависимости величины Uвх от входного сигнала для раз-

δ(Uвх )

личных μ приведены на рисунке 2.4. При увеличении μ расширяется область значений входного сигнала, в которой отношение сигнал-шум квантования приблизительно постоянно при

μ Uâõ 1.

Uвх , дБ

2n 1 δ(Uвх)

δ Uогр 102,65

Uвх, дБ

Рисунок 2.4 – Зависимость Uвх от величины входного сигнала

δ(Uвх )

В современных ЦСП находят применение две логарифмические характеристики компандирования (типов А и μ), которые удобно изображать и описывать в нормированном виде у = f(х),

где А = 87,6 и μ = 255 — параметры компрессии.

29

Характеристика компандирования типа А используется в ЦСП, соответствующих европейской ПЦИ, а типа μ — в ЦСП, соответствующих североамериканской ПЦИ.

Оценим выигрыш от компандирования с А-законом.

Кодеком называют систему КОдер-ДЕКодер, определяющую в ЦСП соотношение между качеством передачи сигнала и скоростью цифрового потока. Импульсно-кодовую модуляцию называют ИКМ-64, так как цифровой поток на один канал имеет скорость fд m = 8 (кГц) 8 (разрядов) = 64 кбит/с. Из регламентированных рекомендаций G.711 и G.712 МСЭ-Т версий ИКМ-64, далее речь пойдёт только о европейской версии ИКМ-64 (A-закон).

Согласованиединамических диапазонов канала и сигнала производят с помощью компрессии сигнала. Поскольку кодер является групповым устройством, компрессия должна быть безинерционной (мгновенной). Мгновенный компрессор представляет собой усилитель с нелинейной амплитудной характеристикой Uвых(Uвх). При А = 1 имеем линейную амплитудную характеристику; чем больше значение параметра А > 1, тем выше степень компрессии.

От аналоговых компандеров (КОМпрессоров + эксПАНДЕРОВ) перешли к цифровой обработке сигнала, приняв сегментированный А-закон. Шкала непрерывного Uвх и квантованного Uвых напряжений представлена на рисунке 2.5. Знак кодируется отдельно от модуля отсчёта (симметричный код), поэтому показана только положительная полуось.

30