Методы оптимизации

81

В данном случае речь идет об итерационных процессах, порождающих последовательность точек x0 ,x1,K,xk , сходящихся к локальному экстремуму функции f (x) в точке x .

На каждом k -м этапе значение xk+1 определяется выражением

где dk – направление перемещения, которое может быть:

•либо градиентом функции в точке xk , т. е. dk = − f (xk );

•либо вычисленным, исходя из направления градиента f (xk );

•либо выбранным произвольно при условии, что это будет направление

спуска. В этом случае должно выполняться неравенство вида

f T (xk ) dk < 0.

Здесь λk – параметр, характеризующий длину шага.

Способ определения dk и λk на каждой итерации связан с особенностями применяемого метода. Обычно выбор λk осуществляется путем решения задачи минимизации f (x) в направлении dk . Поэтому при реализации изучаемых методов необходимо использовать эффективные методы одномерной оптимизации.

Градиентные методы работают следующим образом. Исходя из начальной точки x0 , вычисляют f (x0 ) в точке x0 . Поскольку f (x0 ) указывает

направление наибольшего возрастания ЦФ, снабжаем направление, противоположное градиенту, величиной λ0 и находим следующую точку:

Повторение процедуры дает последовательность точек:

В этом семействе методов следует выделить методы градиента с заданным шагом, в которых заранее задаются значения λk .

Доказано, что построенная последовательность сходится к решению, т. е. xk → x , если выполняются два условия:

Данная процедура (метод расходящегося ряда) может оказаться медлен-

ной.

3.3.1 Метод наискорейшего спуска (метод Коши)

Известный французский математик Огюстен Луи Коши первым использовал аналогичный алгоритм для решения системы линейных уравнений [2].

В широко используемом методе Коши (МК) λk выбираются так, чтобы минимизировать функцию:

на множестве значений λ ≥ 0 (одномерная минимизация).

Алгоритм Коши. Исходные данные – ЦФ и ее градиент, начальная точка x0 , точность по аргументу εx , точность по функции εy .

1.Задать номер итерации k = 0, вычислить f (x0 ).

2.Вычислить направление спуска dk = − f (xk ).

3.Решить задачу

Φ(λ) = f xk − λ f (xk ) → min,

λ≥0

т. е. найти такое λk , что

Φ(λ ) = min f (xk + λd ).

k λ≥0 k

4.Положить xk+1 = xk + λkdk .

5.Если xk+1 − xk ≤ εx и f (xk+1 ) ≤ εy , то положить x* ≈ xk+1 и закончить

вычисления. Иначе выполнить присваивание k = k +1 и вернуться на шаг 2.

·····························································

Будем говорить, что алгоритм A глобально сходится, если для любой выбранной исходной точки x0 последовательность {xk },

порожденная точками xk+1 A(xk ), сходится к точке, удовлетво-

ряющей необходимым условиям оптимальности.

·····························································

83

·····························································

МК обладает глобальной сходимостью, но это не означает

обязательного получения глобального экстремума функции f (x) . Если функция f (x) дважды дифференцируема в стационарной точке x и гессиан 2 f (x ) положительно определен, то x – локальный минимум ЦФ. И только если f (x) является выпуклой функцией, то x является точкой глобального минимума f (x).

·····························································

МК обладает устойчивостью, т. е. при достаточно малом значении λk обеспечивается выполнение неравенства

f (xk+1 )≤ f (xk ).

МК позволяет существенно уменьшить значение ЦФ (быстро спуститься на «дно оврага») при движении из точек, расположенных на значительных расстояниях от точки x , но в дальнейшем может произойти «зацикливание», поэтому МК часто используются совместно с другими градиентными методами (например, методом Ньютона) в качестве начальной процедуры.

Недостаток: для некоторых типов функций сходимость может оказаться медленной. В самом деле, если λk минимизирует функцию

которое доказывает, что последовательные направления ортогональны. В случае ярко выраженной нелинейности («овражности») ЦФ происходит «зацикливание» (см. рис. 3.6).

Несмотря на то что МК не имеет большого практического значения, он реализует важнейшие шаги большинства градиентных методов.

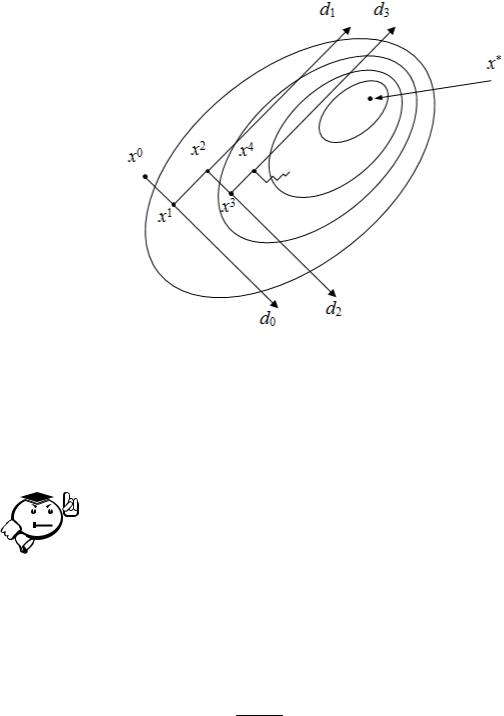
84

Рис. 3.6 – Метод Коши – «зацикливание» траектории спуска

3.3.2 Метод Ньютона

·····························································

В МН и направление, и шаг перемещения фиксированы, т. е. в

формуле (3.25) полагаем:

λk =1, dk = − 2 f (xk ) −1 f (xk ).

·····························································

Эта формула есть не что иное, как МН в применении к решению системы нелинейных уравнений:

∂f (x) = 0, i =1,K,n.

∂xi

Алгоритм Ньютона. Исходные данные – ЦФ, ее градиент и гессиан, начальная точка x0 , точность по аргументу εx , точность по функции εy .

1.Задать номер итерации k = 0, вычислить f (x0 ).

2.Вычислить направление спуска dk = − 2 f (xk ) −1 f (xk ).

3.Положить xk+1 = xk + dk .

85

4. Если xk+1 − xk ≤ εx и f (xk+1 ) ≤ εy , то положить x* ≈ xk+1 и закончить вычисления. Иначе выполнить присваивание k = k +1 и вернуться на шаг 2.

Если f (x) – строго выпуклая функция, то МН сходится за одну итера-

цию.

Недостаток. При использовании МН на каждой итерации возникает необходимость вычисления и последующего обращения матрицы Гессе

2 f (xk ).

3.3.3 Модифицированный метод Ньютона

Если функция f (x) не квадратичная (или не близка по форме к квадратичной функции), то МН не отличается высоким быстродействием и надежностью. В модифицированном МН (ММН) последовательность итераций строится

Выбор параметра λk осуществляется подобно методу Коши – чтобы ми-

на множестве значений λ ≥ 0 (одномерная минимизация). Это гарантирует выполнение неравенства

f (xk+1 )≤ f (xk ).

Если ЦФ строго выпуклая, то ММН, как и МН, сходится за одну итерацию, причем минимизация функции (3.31) дает λ0 =1.

Модифицированный алгоритм Ньютона. Исходные данные – ЦФ, ее градиент и гессиан, начальная точка x0 , точность по аргументу εx , точность по функции εy .

1.Задать номер итерации k = 0, вычислить f (x0 ).

2.Вычислить направление спуска dk = − 2 f (xk ) −1 f (xk ).

3.Решить задачу

86

т. е. найти такое λk , что

Φ(λk ) = minλ≥0 f (xk + λdk ).

4.Положить xk+1 = xk + λkdk .

5.Если xk+1 − xk ≤ εx и f (xk+1 ) ≤ εy , то положить x* ≈ xk+1 и закончить

вычисления. Иначе выполнить присваивание k = k +1 и вернуться на шаг 2. Недостаток: как и в МН, на каждой итерации возникает необходимость

вычисления и последующего обращения матрицы Гессе 2 f (xk ).

3.3.4 Метод Марквардта

Метод Марквардта (ММ) является комбинацией методов Коши и Ньютона. В нем сочетаются положительные свойства обоих методов. Направление поиска в ММ определяется равенством

где E – единичная матрица.

На начальной стадии λ0 присваивается большое значение (например, 104), так что

Таким образом, большим значениям λ0 соответствует направление поиска d0 = − f (x0 ), т. е. направление поиска совпадает с направлением антиградиента, как в методе Коши. Из формулы (3.33) можно заключить, что при умень-

Ньютона.

Если после первого шага получена точка с меньшим значением ЦФ (т. е. f (x1 )< f (x0 )), следует выбрать λ1 < λ0 (например, λ1 = λ0 β , где β >1) и реализовать еще один шаг. В противном случае следует выбрать λ1 > λ0 (например, λ1 = λ0β , где β >1), и вновь реализовать предыдущий шаг.

87

Алгоритм Марквардта. Исходные данные – ЦФ, ее градиент и гессиан, максимально допустимое количество итераций M , начальная точка x0 , начальное значение параметра λ0 , величина изменения шага β , точность по аргументу εx , точность по функции εy .

1.Задать номер итерации k = 0, вычислить f (x0 ).

2.Вычислить направление поиска dk = − H f (xk )+ λk E −1 f (xk ).

3.Положить xk+1 = xk + dk .

4.Проверить выполнение неравенства: f (xk+1 ) < f (xk ). Если оно выпол-

няется, перейти на шаг 5, иначе на шаг 6.

5.Положить λk+1 = λk β и перейти на шаг 7.

6.Положить λk+1 = λkβ и перейти на шаг 2.

7.Если xk+1 − xk ≤ εx и f (xk+1 ) ≤ εy , или превышено допустимое коли-

чество итераций (k ≥ M ), то положить x* ≈ xk+1 и закончить вычисления. Иначе выполнить присваивание k = k +1 и вернуться на шаг 2.

Достоинства ММ. Относительная простота, ЦФ убывает от итерации к итерации, высокая скорость сходимости в окрестности точки минимума x , отсутствует процедура поиска вдоль прямой.

Недостатки. На каждой итерации возникает необходимость вычисления матрицы Гессе H f (xk ) и последующего обращения (иногда неоднократного)

матрицы H f (xk )+ λk E .

Этот метод широко используется при решении задач (например, в регрессионном анализе), в которых функция f (x) может быть записана в виде суммы квадратов, т. е.

i=1

3.3.5 Методы сопряженных градиентов

Ранее рассматривались методы Коши и Ньютона. Отмечалось, что МК эффективен при поиске на значительных расстояниях от точки минимума x и плохо работает в окрестности x , тогда как МН не отличается высокой надежностью при поиске x из удаленной точки, однако оказывается весьма эффек-

88

тивным в тех случаях, когда xk находится вблизи точки минимума. Далее будут рассмотрены алгоритмы, которые обладают положительными свойствами МК и МН и основаны на вычислении только первых производных [2, 6].

Достоинства методов сопряженных градиентов (МСГ): высокая надежность при поиске x из удаленной точки x0 и быстрая сходимость в окрестности x .

1 МСГ для квадратичных функций

Предполагается, что квадратичная функция имеет вид:

f (x) = 12 xT Ax + bT x + c.

Идея метода состоит в последовательном построении направлений d0 ,d1,K,dn−1 , взаимно сопряженных относительно матрицы A ( A-сопряжен- ных). На каждом шаге k направление dk получается как линейная комбинация градиентов − f (xk ) в точке xk и предшествующих направлений (d0,d1,K,dk−1 ), причем коэффициенты линейной комбинации выбираются так, чтобы dk было сопряженным ко всем предшествующим направлениям.

Для удобства введем обозначения:

что выражает свойство квадратичных функций.

Алгоритм МСГ. Исходные данные – квадратичная ЦФ, ее градиент и гессиан, начальная точка x0 , точность по функции εy . Однако в этом алгоритме

точность можно не задавать. Если все вычисления выполняются без погрешностей, то оптимальное решение будет найдено не более чем за n итераций (при этом должно выполняться строгое равенство f (x* )= 0). Поэтому точность

89

можно задавать лишь на тот случай, если вычисления производятся с погреш-

ную оптимизацию для этого не требуется. Учитывая, что критерий останова

и закончить вычисления. Иначе перейти на шаг 6. Если все вычисления проводятся точно, то метод гарантирует нахождение оптимального решения не более

7. Выполнить присваивание k = k +1. Вернуться на шаг 3.

Вцелом, имеем эффективный метод для решения оптимизационных задач

сквадратичными ЦФ.

90

2 Метод Флетчера – Ривза

Флетчер (R. Fletcher) и Ривз (C. M. Reeves) расширили предшествующий метод на случай произвольных функций. В применении к квадратичным функциям он становится равносильным методу сопряженных градиентов.

Достоинство метода Флетчера – Ривза (МФР): скорость сходимости значительно выше классических градиентных методов. Данный метод полезен для решения задач большой размерности.

Алгоритм метода Флетчера – Ривза. Исходные данные – ЦФ и ее градиент, начальная точка x0 , точность по аргументу εx , точность по функции εy .

1.Задать номер итерации k = 0, вычислить f (x0 ).

2.Вычислить начальное направление спуска d0 = − f (x0 ).

3.Решить задачу:

Φ(λ) = f (xk + λd ) → min,

k λ≥0

т. е. найти такое λk , что

Φ(λk ) = minλ≥0 f (xk + λdk ).

4.Положить xk+1 = xk + λkdk .

5.Если xk+1 − xk ≤ εx и f (xk+1 ) ≤ εy , то положить x* ≈ xk+1 и закончить

7. Выполнить присваивание k = k +1. Вернуться на шаг 3.

3 Метод Полака – Рибьера

Метод Полака – Рибьера (МПР) основан на точной процедуре проведения поиска вдоль прямой и на более общем предположении об аппроксимации ЦФ.

Алгоритм метода Полака – Рибьера. Исходные данные – ЦФ и ее градиент, начальная точка x0 , точность по аргументу εx , точность по функции εy .