Математические основы теории систем

131

Характеристическое уравнение, соответствующее дифференциальному

·······································································

3.2.2 Неоднородные уравнения

Предполагая, что входной сигнал r(t) известен, правую часть уравнения (3.10) можно представить как функцию f (t), называемую иногда вынуждающей функцией, и переписать уравнение (3.10) в виде

метода − метод неопределенных коэффициентов и метод вариации (Лагранжа) параметров [10].

Метод неопределенных коэффициентов может быть применен в том случае, если вынуждающая функция f (t) имеет конечное число линейно независимых производных. Функция f (t) в этом случае может быть многочленом целой положительной степени t или состоять из комбинации экспоненциальной, синусоидальной или гиперболической функций. Идея метода состоит в том, что предполагаемое решение представляет собой линейную комбинацию составляющих f (t) и их производных, при этом каждый элемент этой линейной комбинации входит с неопределенными коэффициентами. Далее предполагаемое решение подставляется в уравнение (3.24), а неопределенные коэффициенты выбираются таким образом, чтобы это уравнение удовлетворялось при всех значениях t.

······················· Пример 3.5 ······················

Найти частное решение уравнения

132

Правая часть уравнения – это сумма константы 1 и экспоненты e−t . Производная константы – нуль, производная экспоненты – та же экспонента, поэтому предполагаемое решение представляем в виде суммы двух слагаемых, первое из которых умножаем на неопределённый коэффициент A, а второе – на B:

·······································································

В том случае, когда отдельные члены в точности совпадают по виду с ка- кой-либо составляющей решения однородного уравнения, процедура ре-

шения предполагает в общем случае умножение на t соответствующих составляющих в выражении для yн (t). Подобная схема сохраняется, когда член f (t)

содержит дополнительный множитель tn . Если же какой-либо член f (t) соответствует кратному корню характеристического уравнения (например, кратности m), то соответствующий член в yн (t) следует умножить на tm .

······················· Пример 3.6 ······················

Найти частное решение уравнения

d2 2y + 2 dy + y = e−t . dt dt

Правая часть уравнения – e−t , и частное решение следовало бы представить в форме yн (t) = Ae−t , но обратив внимание на левую часть уравнения, замечаем (см. пример 3.3), что общее решение однородного уравнения имеет вид

133

yо (t) = c1e−t + c2te−t ,

поэтому предполагаемое частное решение нужно умножить на t2 : yн (t) = At2e−t . Определив производные

dydtн = (2At − At2 )e−t ,

d2 y2н = (2A− 4At + At2 )e−t , dt

и подставив все необходимое в исходное дифференциальное уравнение, получим:

(2A − 4At + At2 )e−t + 2(2At − At2 )e−t + At2e−t = e−t .

Приведя подобные члены в последнем уравнении, получим 2Ae−t = e−t ,

откуда с очевидностью имеем A = 12 и, таким образом, yн (t) = t22 e−t .

·······································································

Метод вариации параметров может быть применен для любых функций f (t) независимо от того, имеет или не имеет эта функция конечное число независимых производных. Также этот метод может быть применен и для нестационарных систем, когда коэффициенты ai уравнения (3.10) зависят от времени.

По методу вариации параметров частное решение определяется на основе составляющих решения однородного уравнения, предполагая, что это решение уже известно.

В уравнении первого порядка

135

Одно из условий – это удовлетворение уравнения (3.30) при подстановке (3.32), а второе можно выбрать любым наиболее удобным образом. Запишем, например, yɺн :

Уравнение (3.33) возьмем в качестве второго условия. Определяя производные yɺн , ɺɺyн и подставляя их в уравнение (3.30), получим

a0 (u1ɺɺy1 + uɺ1 yɺ1 + u2 ɺɺy2 + uɺ2 yɺ2 ) + a1 (u1 yɺ1 + u2 ɺɺy2 ) + a2 (u1y1 + u2 y2 ) = f . Перегруппируем

a0 (uɺ1yɺ1 + uɺ2 yɺ2 ) + u1 (a0 ɺɺy1 + a1 yɺ1 + a2 y1 ) + u2 (a0 ɺɺy2 + a1 yɺ2 + a2 y2 ) = f . Учитывая, что y1 и y2 удовлетворяют уравнению (3.31), имеем

Совместное решение (3.33) и (3.34) по правилу Крамера дает:

Знаменатель выражений (3.35), являющийся вронскианом уравнения (3.31), отличен от нуля, так как решения y1 и y2 линейно независимы, и, следовательно, решения uɺ1, uɺ2 всегда существуют. Интегрируя (3.35), получаем u1, u2 и частное решение в форме (3.32).

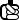······················· Пример 3.8 ······················

Найти частное решение уравнения

d2 2y + 2 dy + y = e−t dt dt

из примера 3.6 методом вариации параметров.

Общее решение соответствующего однородного уравнения (см. пример 3.3):

yо (t) = c1e−t + c2te−t , так что y1 = e−t , y2 = te−t . Подсчитаем вронскиан:

V (t) = y1yɺ2 + yɺ1 y2 = e−t (e−t − te−t )+ e−t (te−t )= e−2t .

137

Из примеров (3.19)–(3.22) видно, что метод неопределенных коэффициентов зачастую проще метода вариации параметров, однако последний метод более общий, поскольку не имеет ограничений на правую часть уравнения.

3.2.3 Вычисление постоянных интегрирования

Произвольные постоянные в решении однородного уравнения вычисляются на основе начальных или граничных условий. В большинстве случаев для решения дифференциального уравнения n-го порядка при определении по-

водных заданы непосредственно после момента t0 . Очень часто полагают t0 = 0 . Начальные условия обычно определяются, исходя из запасенной системой энергии к моменту t = t0+ . Очень важно, что постоянные интегрирования зависят также от вынуждающей функции и не могут быть определены, пока не найдена составляющая решения yн (t).

В ряде важных случаев начальные условия нулевые. Для уравнения n-го

и для получения общего решения, удовлетворяющего нулевым начальным условиям (3.38).

Действительно, возьмем, например, уравнение первого порядка. Объеди-

Верхний предел в (3.39) соответствует частному решению, а нижний предел дает постоянную интегрирования в решении однородного уравнения. Причем из (3.39) следует, что y(t0 ) = 0 .

В общем случае уравнения n-го порядка при нулевых начальных условиях из выражений (3.36) и (3.37) следует:

138

y(t) = y1 (t)(u1(t) − u1(t0 )) + ...+ yn (t)(un (t) − un (t0 )) =

3.3 Методы преобразований

Выше было рассмотрено описание сигналов и систем во временной области, то есть в зависимости от непрерывного времени t. Альтернативной формой математического описания является частотное описание.

3.3.1 Интегральное преобразование Фурье

Переход в частотную область производится с помощью интегрального преобразования Фурье:

−∞

где f (t) однозначная, содержащая конечное число максимумов, минимумов и разрывов функция.

Кроме того, для существования интеграла (3.40) требуется абсолютная интегрируемость функции f (t), то есть выполнение условия:

изображением является взаимно-однозначной, то есть по частотному спектру

Эти выражения определяют косинус-преобразование Фурье.