
Техническая электродинамика, Основы электродинамики и распространение радиоволн, Антенны и устройства СВЧ
..pdf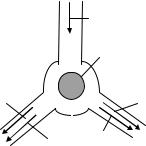
|
|
|
101 |
|
Во многих случаях циркуляторы используются в качестве вентилей для |
||
|
1 |
|
устранения волны, отраженной от нагрузки. Энер- |
|
E1 |
|
гия отраженной волны поглощается не в феррито- |
|
|
|
вом элементе, а во внешней поглощающей нагруз- |
|
феррит |
ке подключенной к плечу 3, что очень важно на |
|
Е’21 |
|
Е’31 |
высоком уровне мощности. Систему охлаждения |
|
легче осуществить в схеме с циркулятором т. е. с |
||
2 |
|
3 |
внешней нагрузкой, чем ферритового элемента, как |
Е21 Е31 |
в случае вентиля. Простейший циркулятор пред- |
||
|
|
|
|
ставляет собой трехплечий мост, плечи которого повернуты друг относительно друга на 120 . В центре такого волноводного сплетения расположен ферритовый цилиндр (высота его не обязательно равна высоте волновода), намагниченный вдоль своей оси, т.е. в направлении, перпендикулярном широким стенкам прямоугольного волновода, либо перпендикулярно плоскости полоска. Если рассматриваемый волноводный элемент не содержит феррита, то поступающая энергия из канала 1, делится поровну между каналами 2 и 3. При этом КСВ со стороны канала 1 равно 2, так как к нему подключены два идентичных канала с одинаковыми Zв . Иначе
говоря, волновод 1 нагружен на сопротивление, равное половине Zв .
При наличии намагниченного феррита можно считать, что волны, проходящие в каналы 2 и 3, являются результатом суперпозиции двух полей,
первичного |
E |
21 |
и |
E |
31 |
и переизлученного ферритовым цилиндром |
E |
и |
E |
. |
|
|
|
|
|
21 |
|
31 |
|
Первичные поля в каналах 2 и 3 в силу симметрии системы синфазны и равны по амплитуде. Амплитуда и фаза вторичного поля зависят от размеров и параметров намагниченного феррита. Оказывается, что эти величины можно подобрать так, чтобы поля E 21 и E 21 в канале 2 были синфазны, а поля E 31
и |
E |
в канале 3 противофазны. Если, кроме, того, обеспечено равенство этих |
|
31 |
|
полей по амплитуде, то энергия волны из канала 1 будет полностью передаваться в канал 2. Очевидно. что в силу симметрии системы волна из канала 2 будет попадать в канал 3, а из канала 3- снова в канал 1.
Следует отметить, что в таком режиме система будет согласованна со стороны трех плеч, так как, например, канал 1 будет подключен только к каналу 2, т. е. нагружен на сопротивление Zв .
Для расчета циркулятора используется метод, основанный на анализе матрицы рассеяния. Это возможно, поскольку на практике учитывается только результирующий эффект в линии передачи на некотором расстоянии от феррита и исключающий из рассмотрения область перехода от однородной линии передачи к ферритовой неоднородности.
Преимущества использования матрицы рассеяния обусловлены тем, что элементы этой матрицы связывают только амплитуды отраженных и прохо-

102
дящих волн в различных линиях, входящих в циркулятор и выходящих из него.
В общем случае, амплитуды b n отраженных волн и амплитуды a n падающих волн связаны линейным соотношением вида
|
|
|
|
b S a |
|
|
|
Элементы матрицы рассеяния S не зависят от амплитуды и времени (эти |
|||
переменные входят в величины |
|
|
|
a и b ). Амплитудные коэффициенты а и b ха- |
|||
рактеризуют падающую и отраженную волны, распространяющихся в линии передачи энергии вдоль выбранной оси Z. Можно ввести коэффициент отра-
жения Г ,
|
|
|
|
j z |
|
|
|
|
Г |
|
b e |
|
|
b |
e2 j z |
||
a e j z |
a |
|||||||
|
|
|
|
|||||
|
|
|
a , или в более общем виде |
|||||
При Z = 0, b Г |
||||||||
bi |
Sii |
a i |
|
|
|
|||
где b i - амплитуды волны, выходящей из i-го плеча сочленения (циркулятора), когда в это плечо падает волна с амплитудой a i , Sii - коэффициент отра-
жения; он равен нулю, когда плечо согласованно, т. е. отраженного сигнала нет. Такой подход дает возможность выразить выходную волну в i-м плече, обусловленную, кроме входной волны в этом плече, также и добавочной входной волной a j в j-м плече
bi Sii ai Sij a j
где Sij - коэффициент передачи для волны, входящей в j-е плечо сочленения с амплитудой a j и выходящей из i-го плеча с амплитудой Sij a j .
Обобщая для n плеч, имеем
b1 S11 a1 S12 a 2 S1n a n ,
b2 S21 a1 S22 a 2 S2n a n ,
bn Sn1 a1 Sn 2 a 2 Snn a n ,
или в матричном представлении
b1 S11S12 S1n a1
b2 S21S22 S2n a 2 ,
bn Sn1 Sn 2 Snn a n

103
которое сокращенно записывается в виде
|
bi |
Sij a j |
|
|
j |
или |
|
|
b |
S a |
Определение матрицы рассеяния предполагает, что выполняются усло-
вия:
1. Каждый волновод может рассматриваться как линия, в которой распространяется только один тип волн, характеризуемый единственной фазовой постоянной.
2.Амплитуды а и b электромагнитных полей, распространяющихся в волноводах вдали от сочленения, нормируются таким образом, что амплитуде
а=1 соответствует единичная мощность, проходящая через линию передачи. При этом элементы матрицы рассеяния не зависят от характеристических сопротивлений линии передачи различного вида.
3.Сочленение линейно и пассивно. Если сочленение взаимно, то Sij S ji
для невзаимного устройства.
4. Элементы матрицы рассеяния, описывающей сочленение (циркулятор), должны удовлетворить закону сохранения энергии.
Закон гласит, что полная мощность Рвх, поступающая во все плечи пассивного сочленения, должна быть равна сумме мощности, поглощенной в сочлении, и мощности, выходящей из всех плеч:
Pвх Pвых 12 i a i a i bi bi 0
Эта разность должна быть равна мощности рассеянной в сечении. Рассеиваемая мощность обусловлена электрическими и магнитными потерями в сочлении и всегда положительна, кроме случая отсутствия потерь, когда она равна нулю. Поскольку
|
bi Sij a j |
и |
|
|
b Sij a j то |
||||||
|
|
j |
|
|
|
|
|
|
|
j |
|
|
|
|
|
a |
|
S |
|
S |
a a |
|
|
|
|
a |
i |
ij |
0 |
||||||
|
|
|
i |
|
|
ij |
j |
ђ |
|||
|
|
i |
|
|
|
jђ |
|
|
|
|
|
или в матричной форме |
|
|
|
|
|
|
|
|
|||
|
|
~ |
|
|
|
|
|
|
|
|
|
|
a 1 |
S S 0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
- вектор-столбец падающих волн. |
||||||
где 1- единичная матрица, а |
|
a |
|||||||||
Символ |
~ |
|
|
|
|
|
|
|
|
|
|
S обозначает транспонированную матрицу S, в которой строки и |
|||||||||||
столбцы поменялись местами. При отсутствии потерь в сочленении
~
S S 1.
Это означает, что элементы матрицы рассеяния, описывающей сочленение без потерь, должны удовлетворять соотношениям

|
|
104 |
Siк S jк |
1, |
при i j |
|
при i j |
|
к |
0, |
Матрица S, удовлетворяющая этим условиям называется унитарной матрицей. Таким образом, из закона сохранения энергии следует, что сочленение без потерь описывается унитарной матрицей рассеяния.
По теореме Кэрлин, любое согласованное невзаимное трехплечевое СВЧ сочленение без потерь является идеальным циркулятором. Действительно, матрица рассеяния симметричного трехплечевого сочленения без потерь может быть записана в виде
О В С S С О В В С О
Если матрица унитарна, то В 2 С 2 1
ВС 0
Отсюда следует, что либо
В 0, |
|
C |
|
|
1 |
||
|
|
|
|||||
либо |
|
|
|
|
|
|
|
C 0, |
|
|
В |
|
1 |
||
|
|
|
|||||
|
|
|
|
|
|
|
|
Первое условие есть условие существования идеального симметричного циркулятора с направлением циркуляции по часовой стрелке. Тогда
0 01 S 10 0 010
Второе условие приводит к матрице рассеяния циркулятора с противоположным направлением циркуляции, т. е. при изменении направления подмагничивающего магнитного поля на противоположное.
5.6.2Порядок выполнения работы
-Получить зачет по теоретической части (глава 3).
-Изучить принцип работы прибора типа Р2.
-Собрать экспериментальную установку (рисунок 4.3 и рисунок 4.4).
-Прокалибровать установку согласно инструкции к прибору типа Р2.
-Измерить коэффициент прохождения по схеме 2 3 и 3 2 1.
-Определить развязку между плечами 1 3; 2 1.
-Оценить погрешность измерения.(Исходные данные для определения погрешностей взять из инструкции к прибору).
-Оформить отчет.
105
5.6.3Контрольные вопросы для самоподготовки
-Поперечное распространение ЭМВ в намагниченном феррите.
-Обыкновенная и необыкновенная волна.
-Тензор магнитной проницаемости для необыкновенной волны.
-Физические основы создания ферритовых циркуляторов.
-Основные параметры циркулятора.
-Методика измерения параметров циркулятора.
5.7Исследование параметров СВЧ резонаторов
Цель работы. Теоретическое и экспериментальное исследование микрополосковых СВЧ резонаторов, расчет на заданный диапазон частот одномодовых резонаторов и анализ схем включения в передающий тракт.
5.7.1 СВЧ резонаторы и их основные параметры
Резонатор СВЧ представляет собой некоторый объем, ограниченный проводящими либо отражающими поверхностями или другими неоднородностями, способными удерживать электромагнитные поля, благодаря чему в нем могут возбуждаться и поддерживаться периодические колебания. Поскольку эти колебания локализованы в ограниченной части пространства, иногда все резонаторы СВЧ называют объемными, чаще же под объемными понимается только резонатор, который образуется внутри хорошо проводящей металлической оболочки.
Воболочке объемного резонатора имеется одно-два небольших отверстия (окна связи) для осуществления связи с линиями передачи, тем не менее, её в большинстве случаев можно рассматривать как замкнутую (связь с внешними волноводами мала).
Впоследнее время в технике СВЧ находят все более широкое применение диэлектрические, ферритовые, запредельные (предельные) и открытые резонаторы.
Объем, в котором сосредоточены колебания у диэлектрических и ферритовых резонаторов, ограничен практически поверхностью раздела диэлек- трик-воздух, феррит-воздух.
Отличительной особенностью запредельных и открытых резонаторов является отсутствие, как замкнутой поверхности, так и границ раздела между разными средами. Тем не менее, колебания в этих резонаторах также локализованы в некотором конечном объеме.
По способу включения в тракт резонаторы могут выполнять либо роль оконечных нагрузок (двухполюсник), либо проходных элементов (четырехполюсник).

106
В отличие от двух - и четырехполюсников для описания работы резонаторов, помимо матрицы рассеяния, вводятся параметры, f0 - резонансная частота и Q -добротность.
Величина f0 определяется геометрическими параметрами резонатора и структурой электромагнитного поля. Резонатор СВЧ имеет бесконечное количество "резонансных" частот, но обычно интересуются одной из них f0 - связанной с определенными типами колебаний, обычно это основной тип колебаний.
Добротность резонатора определяется как отношение запасенной энергии за период к растрачиваемой энергии за период
Q 2 Wз Wnт
Энергию потерь можно выразить через среднюю по времени мощность потерь
Wnт Pn с р Т , тогда
Q Wз .
Pn с р
Потери энергии в резонаторе складываются из мощности потерь в стенках резонатора - омические потери, Pr , потерь в диэлектрическом заполнении
Pд , и потерь во внешних цепях Pсв , тогда
Pn с р Pr Pд Pсв .
Добротность резонатора, вычисленная с учетом только потерь в объеме резонатора (омические потери в стенках и диэлектрические потери в объеме), называется собственной добротностью Q0.Добротность, определенная с учётом собственных потерь и потерь во внешних цепях, называется нагруженной добротностью Qн, которые связаны соотношением
1 1 1
Qн Q0 Qвн
где внешняя добротность будет
Qвн Wз
Pср св
В качестве параметра, характеризующего связь резонатора с внешними цепями, вводится коэффициент связи определяемый как
|
Q0 |
|
Pсв |
|
Pсв |
. |
|
|
|
|
|
||||
|
Q |
вн |
|
P |
|
P P |
|
|
|
|
n с р |
|
r д |
||
Откуда, когда имеется одна связь с внешними цепями
Q
Qн 1 0 .
В случае, когда два элемента связи (четырехполюсник)

107
Qн Q0 , 1 1 2
где 1 и 2- коэффициенты связи с входным и выходным трактами. Коэффициент передачи по мощности через резонатор при резонансе
|
T 0 |
|
2 |
|
|
4 1 |
2 |
|
|
|
|
|
|
||||||
|
|
|
1 |
|
2 |
2 |
|||
|
|
|
|
|
|||||
|
|
|
|
|
|
1 |
|
|
|
В режиме свободных колебаний, добротность является мерой способности резонатора сохранять запасенную энергию
|
t W 0 e |
о |
t |
W |
Q |
||
з |
з |
|
|
где Wз 0 - энергия, запасенная в начальный момент времени.
В режиме вынужденных колебаний добротность можно рассматривать как меру скорости изменения реактивной проводимости контура на частотах, близких к резонансной
Q |
0 |
dB |
|
|
|||
|
|
|
|
|
|
, |
|
|
|
|
|||||
|
|
|
|
||||
|
2 |
G d |
|
0 |
|||
где G и В активная (резистивная) и реактивная составляющие проводимости резонатора.
Измерение значений добротности резонатора, как правило, сводится к измерению частот, временных интервалов, значений КСВН, коэффициентов отражения или передачи по мощности.
5.7.2 Измерение добротности по декременту колебаний
Метод измерения добротности по декременту колебаний основывается на наблюдении явления затухания собственных колебаний в резонаторе. Постоянная времени этого затухания определяет значение добротности Q.
Пусть J0 - сила тока в резонаторе в момент выключения источника сигнала, вид которого задается генератором работающим в импульсном режиме. Закон изменения тока по времени с. момента прекращения воздействия можно записать в виде
J t |
|
|
|
e |
t |
|
|
|
|
||||
J |
0 |
2 Qн |
. |
|
|
|
|
||||||
Если ток J t |
|
|
|
|
|
|
|
|
|
|
|
||
|
измеряется для двух следующих друг за другом моментов |
||||||||||||
времени t1 , и t2, то отношения этих значений запишется |
|||||||||||||
|
J t1 |
|
|
|
|
|
|
|
|
||||
|
e |
|
t1 t2 |
|
e |
|
t |
||||||
|
2 Qн |
2 Qн |
|||||||||||
|
J t |
|
|
|
|
|
|
|
|
|
|
|
|
2
где t t 2 t1 . Отсюда
108
Q’ |
|
f t |
|
||
|
|
|
|
||
J t |
|
|
|
||
|
|
|
|||
|
|
n |
1 |
J t |
|
|
|
|
|
|
2 |
Если t соответствует отрезку времени, в течение которого ток умень-
шается в е раз, то
Qн f t .
5.7.3 Измерение добротности резонатора, включенного как оконечная нагрузка
Этот метод измерения добротности резонатора основан на измерении его параметров как двухполюсника в окрестности резонансной частоты.
Определение добротности по измеренным значениям входного сопротивления и КСВН осуществляется, как правило, с помощью измерительной линии или измерителей входного сопротивления.
СВЧ резонатор можно представить в виде эквивалентного колебательно-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
го контура с сосредоточенными параметра- |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ми. Предположим, что на зажимах этого эк- |
|||||||||
G н |
|
G 0 |
|
|
C |
|
|
|
L |
|
|
|
|
|
вивалентного контура действует напряжение |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
U |
|
e i o t , где |
|
|
L C 12 - |
резонансная |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
круговая частота. Значение запасенной энер- |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
гии |
|
в контуре |
|
Wз можно |
определить, |
||||
например, по формуле: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
W |
1 |
C U |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
з |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обозначив полную проводимость контура, как |
Y G i B и учитывая, что |
|||||||||||||||||||||||||||||
|
|
|
|
B C |
|
1 |
|
|
|
; |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
dB |
|
|
C |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
d |
2 |
L |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
dB |
|
|
|
|
|
|
|
C |
1 |
|
|
2 C |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
d |
|
0 |
2 L |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
U02 |
|
|
dB |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Wз |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
4 |
|
d |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||||||||||
Потери энергии в контуре за один период колебаний составляют |
||||||||||||||||||||||||||||||
|
|
|
|
Wb 0T Uo2 |
G sin 2 ( t) dt |
|
G Uo2 |
|
||||||||||||||||||||||
|
|
|
|
0 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
109 |
|
и добротность будет |
|
|
|
|
|
|
|
0 |
|
|
B |
|
|
Q |
|
|
|
|
|
. |
|
||||||
|
|
|||||
|
2 G |
|
|
|
|
0 |
Рассматривая в качестве G ту или иную составляющую активной проводимости контура, получим соответствующие значения добротности
|
|
|
|
0 |
|
|
dB |
|
|
|
|
||||||
Q |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
; |
|||
2 |
G |
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||||
|
|
|
|
|
|
d |
0 |
||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
dB |
|
|
||||
Q |
‰’ |
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
||
2 Y0 |
|
|
|
||||||||||||||
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
d |
|
0 |
||||||||
|
|
|
|
|
0 |
|
|
|
|
dB |
|
|
|
|
|
Q’ |
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
G Y0 |
|
|
||||||||
|
|
|
|
|
|||||||||
|
|
|
2 |
|
|
d |
|
0 |
|||||
где Y |
1 |
- активная проводимость внешней цепи, равная волновой прово- |
|||||||||||
|
|||||||||||||
0 |
Z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
димости подсоединенного к резонатору волновода. Для резонатора с достаточно высокой добротностью можно записать
|
|
dB |
|
B |
|
B1 |
B2 |
|
|
|
|
|
|
|
|
, |
|||
|
|
1 |
2 |
||||||
|
|
d |
|
|
|
|
|||
что для частот 1 и 2 |
соответствует выполнению условия |
||||||||
B G Y0 |
|
|
|
||||||
где
вия
S
S1,2
S0
Тогда |
|
|
|
|
2 G Y0 |
|
|
|||
dB |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
. |
|
|
|
1 2 |
|
|
|
|||||
|
|
|
|
|
|
|||||
d |
|
o |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Подставляя в выражение для добротности, получим |
|||||||||||||||||
Q |
|
|
|
0 |
|
|
2 |
G Y0 |
|
|
|
f0 |
|
f0 |
, |
||
|
|
|
|
|
|
|
|
|
|
|
|||||||
н |
|
G Y0 |
|
|
|
|
|
|
|
||||||||
|
2 |
|
|
1 2 |
|
|
|
|
|
f1 f2 |
|
f |
|||||
|
|
|
|
|
|
|
|
|
|
||||||||
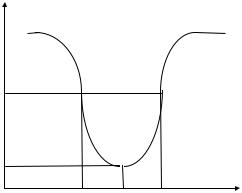
- f1,f2 - точки резонансной кривой, соответствующие выполнению усло- B G Y0 . На рис. представлен типичный вид зависимости КСВН в
линии, нагруженной резонатором, от частоты возбуждающих колебаний. Минимум КСВН соответствует собственной частоте резонатора.
КСВН при резонансе S0 не равен нулю, как следует из рис. Действительно, коэффициент стоячей волны по напряжению S и коэффициент отражения Г по напряжению связан соотношением
f1 |
f0 |
f2 |
f |

110
S |
|
1 |
|
|
Г |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
|
Г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y0 Y |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
Г |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
Y Y |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
Y G 0 B 0 |
|
|
|
||||||||||||
На частоте резонанса, где |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
Y0 |
G 0 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
Y |
|
G |
0 |
|
|
|
Y |
|
|
|
|
|||||||||||||
S |
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
при Y |
G |
, |
||||||||||||||
0 |
|
|
|
|
|
G 0 |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y0 |
|
G |
|
0 |
|
0 |
|
|||||||||
|
|
|
|
|
|
1 |
|
|
0 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
Y |
|
G |
0 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
1 |
G 0 Y0 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
G |
0 |
|
Y |
|
G |
0 |
|
|
|
|
||||||||||||||
S |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
при Y |
G |
|
|
|||||||||||
0 |
|
|
|
|
|
|
Y0 |
|
|
0 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G 0 |
|
|
Y |
0 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
1 G |
|
|
Y |
|
|
0 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
Таким образом, КСВН в линии на частоте резонанса может характеризо- |
||||||||||||||||||||||||||||||
вать отношение |
|
|
Y0 |
G 0 |
|
либо |
G 0 |
|
Y0 , и, как отсюда следует, важной харак- |
|||||||||||||||||||||
теристикой, различающий эти два случая, является коэффициент отражения Г
на частоте резонанса. Условие |
G 0 Y0 соответствует критической связи |
||||||||
(Г=0). При G 0 Y0 |
(связь меньше критической, ), |
||||||||
S |
|
|
G 0 |
|
1 |
, |
Г 0 ; |
||
0 |
|
|
|
||||||
|
|
|
Y0 |
|
|
|
|||
|
|
|
|
|
|
||||
при G 0 Y0 (связь больше критической, >1 ) |
|||||||||
S |
|
|
Y0 |
|
, |
Г 0. |
|||
0 |
|
||||||||
|
|
|
G0 |
|
|
|
|
||
|
|
|
|
|
|
|
|
||
Знак коэффициента отражения Г может быть определен экспериментально следующим образом. Полностью отстроив резонатор (или изменив частоту генератора относительно резонансной частоты) находят положение узла при расстройке. Положение зонда в узле соответствует его подключению "к зажимам" эквивалентного резонатору параллельного контура. Теперь настройка резонатора в резонанс производится по максимуму напряжения на зонде. После настройки резонатора (источника сигнала) в резонанс перемещение зонда относительно положения узла при расстройке покажет, что в том положении расположен или максимум или минимум напряжения, так как сопротивление резонатора при резонансе чисто активное. Если этот эксперимент покажет наличие минимума - связь меньше критической, если наличие максимума - больше.
