Основы физической оптики

171

Вкладом механизма диффузии, как отмечалось, пренебрегаем, так как его следует учитывать при Λ <5¸2 мкм. Это обусловлено обратно пропорциональной зависимостью величины диффузионного поля и пространственного периода световой интерференционной картины, что иллюстрируется соотношением (7.37).

При формировании фоторефрактивных решеток возможны два режима: а) короткозамкнутый кристалл; б) разомкнутый кристалл.

Рассмотрим второй случай, который ближе к реальности. Для разомкнутого кристалла ток проводимости в цепи отсутствует, т.е. выполняется условие:

Для определения констант интегрирования А и С используем условия, определяющие величину поля Esc в начальный момент времени t=0 после «включения» светового поля, и значение Esc в стационарном режиме. Первое из них – Еsc(0)=0 дает: A + C = 0, откуда получаем: А = – С. Итак, решение для Еsc теперь имеет вид:

где t = sε – время Максвелловской релаксации электрического заряда в среде.

Данное соотношение описывает временную эволюцию наведенного поля пространственного заряда Esc в процессе записи фоторефрактивной решетки в среде с фотовольтаическим механизмом транспорта носителей заряда при сделанных предположениях. Как уже отмечено, удельная проводимость среды характеризуется двумя составляющими – темновой проводимостью σ d и

173

Из приведенного соотношения видно, что возмущенная часть показателя преломления среды состоит из двух составляющих: постоянной, не зависящей от координаты z, и переменной, с гармонической зависимостью от этой координаты.

7.3.5.Некоторые характеристики ФРЭ и фоторефрактивных материалов

Важными характеристиками фоторефрактивных кристаллов являются фоторефрактивная чувствительность, дифракционная эффективность и время записи – релаксации ФР решеток, определяющее, в конечном итоге, время

хранения голографической информации.

Понятие чувствительности характеризует величину световой энергии, необходимой для записи информации в фоторефрактивном кристалле. Она определяется следующим образом:

где Wl – полная энергия светового поля, необходимая для записи одиночной решетки на площади в 1 см2; m – видность (контраст) интерференционной картины. Голографическая чувствительность измеряется в см2/Дж.

Дифракционная эффективность фоторефрактивных решеток

определяется формулой Когельника:

характеристикой, поскольку оно определяет возможности материалов для их использования в качестве среды для долговременного хранения голографической информации или для нужд динамической голографии, где требуется как можно более быстрый отклик на изменения светового поля.

Некоторые характеристики для наиболее перспективных фоторефрактивных материалов представлены в таблице 7.5.

174

175

8. ЭЛЕМЕНТЫ НЕЛИНЕЙНОЙ ОПТИКИ

Как известно, материальная среда проявляет нелинейные свойства в отношении некоторого воздействия, если ее физические характеристики зависят от величины этого воздействия. Соответственно, оптическая нелинейность наблюдается при зависимости диэлектрической проницаемости материалов от интенсивности света. В долазерную эпоху нелинейно– оптические эффекты в экспериментах практически не наблюдались (если не считать линейный и квадратичный электрооптические эффекты, которые, как будет отмечено далее, могут быть отнесены к нелинейно– оптическим явлениям). Было известно, что световые пучки в вакууме проходят друг сквозь друга, без какого – либо взаимодействия. Этот факт рассматривался как бесспорная иллюстрация применимости принципа суперпозиции, являющегося следствием линейности уравнений классической оптики, к рассмотрению световых волн. С квантовых позиций отсутствие взаимодействия световых пучков свидетельствовало о невозможности непосредственного взаимодействия фотонов. Предполагалось, что принцип суперпозиции остается справедливым и при распространении света в материальной среде.

Линейность оптических явлений в долазерный период закономерна, поскольку для известных некогерентных источников света величина напряженности электрического поля не превышает 102÷103 В/м. Это значительно меньше напряженности внутриатомных электрических полей (109 ÷ 1012 В/м), поэтому отклик среды на такое световое поле оказывается линейным. Для лазерного излучения величина напряженности электрического поля может достигать 109 – 10 10 В/м, что уже сопоставимо с напряженностью внутриатомных полей. А это означает, что при прохождении световой волны такой амплитуды через вещество, его поляризуемость и, соответственно, высокочастотная диэлектрическая проницаемость, могут изменяться – они зависят от амплитуды воздействующего светового поля. Среда является в этом случае нелинейной, а уравнения электромагнитного поля также становятся нелинейными [3, 5-8, 13].

Появление мощных лазеров позволило наблюдать и изучить целый ряд нелинейно– оптических явлений и стимулировало развитие нелинейной оптики. Таким образом, возможность проявления нелинейно– оптических свойств материала зависит от величины интенсивности света. Одна и та же среда может рассматриваться как линейная при малых интенсивностях света и как нелинейная – при больших.

176

8.1. Элементы теории нелинейно – оптических явлений

8.1.1. Квадратичная и кубичная оптические нелинейности.

Рассмотрим диэлектрическую восприимчивость среды c. Из курса электродинамики известно, что она связывает величину поляризации среды, индуцированной полем электромагнитной волны, с величиной напряженности этого поля. В случае изотропного материала эта связь определяется соотношением:

анизотропной среды коэффициент c связывает между собой два вектора, поэтому он является тензором второго ранга. Для понимания различия между нелинейностями разного типа в рамках данного описания тензорный характер c не принимается во внимание и далее, если это не приводит к принципиальным ошибкам, математические выражения записываются для простоты в скалярной форме [5, 13].

Соотношение (8.1) – одно из классических материальных уравнений. Если коэффициент c не зависит от напряженности светового поля, то рассматриваемая среда является линейной. Для лазерного излучения, в случае высокой его интенсивности, невозможно ограничиться только линейным приближением. Выражение для диэлектрической восприимчивости c должно быть представлено в этом случае в более общем виде, учитывающем ее зависимость от напряженности электрического поля световой волны:

функциональной зависимости ее поляризуемости от напряженности поля световой волны. При этом соотношение (8.1) принимает форму:

Таким образом, отклик среды (величина P) на поле световой волны (E) оказывается нелинейным. Коэффициенты c( 2 ) , c( 3 ) называют нелинейными восприимчивостями (квадратичной и кубичной, соответственно), а среды, для которых соответствующие слагаемые в (8.3) доминируют, называют средами с квадратичной или кубичной оптической нелинейностью. Нелинейностями более высокого порядка в разложении (8.2), как правило, пренебрегают, в силу малости каждого последующего члена по сравнению с предыдущим. Важно отметить, что квадратичная оптическая нелинейность может проявляться лишь в средах без центра симметрии. Действительно, в центросимметричной среде диэлектрическая восприимчивость c(E) не

177

должна измениться при замене направления поля E на противоположное, т.е. при изменении знака E. Поскольку c( E ) = c( 1 ) + c( 2 ) × E + c( 3 ) × E 2 , то

выполнение последнего условия возможно лишь при c( 2 ) = 0 . Таким образом, в центросимметричной среде низшим типом оптической нелинейности является кубичная нелинейность.

Следует отметить, что под термином «нелинейная оптика» понимается совокупность явлений, в основе которых лежат обратимые процессы изменения характеристик среды. Подобные изменения исчезают после «выключения» света. Таким образом, эффекты необратимых изменений среды, проявляющихся также в сверхсильных световых полях (например, оптический пробой) к области нелинейной оптики не относят, а рассматривают в отдельных разделах физики.

8.1.2. Возможные типы нелинейно– оптических эффектов в средах с квадратичной и кубичной нелинейностью

Поляризация, наводимая световой волной в среде, определяется соотношением:

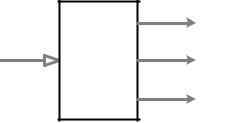
Таким образом, квадратичная нелинейность приводит к возникновению составляющих поляризации на удвоенной частоте светового поля, а также на нулевой частоте. Постоянная поляризация дает возможность оптического детектирования светового поля, а поляризация на удвоенной частоте – возможность генерации его второй гармоники. Типы возможных нелинейно – оптических эффектов в среде с квадратичной нелинейностью иллюстрирует рис. 8.1, где представлены частотные составляющие наведенной поляризации квадратично – нелинейной среды при воздействии гармонического светового поля.

(2)

Рис. 8.1.

179

Таким образом, при распространении монохроматической световой волны в среде с кубичной нелинейностью, возникают составляющие поляризации на той же самой частоте и на ее третьей гармонике (рис. 8.2).

означает изменение диэлектрической проницаемости (или показателя преломления) среды, что является причиной эффектов самовоздействия световых полей. Составляющая поляризации на утроенной частоте обусловливает возможность генерации третьей гармоники основной волны.

Часто среды с кубичной оптической нелинейностью называют керровскими средами. Такое название связано, в частности, с тем, что квадратичный электрооптический эффект (или эффект

Керра) наблюдается в средах с центром симметрии, т.е. в средах с кубичной нелинейностью. Как и в случае среды с квадратичной нелинейностью, можно

показать, что при воздействии на среду с кубичной нелинейностью гармонического светового и постоянного электрического полей, при произвольной малой амплитуде светового поля, в среде появляется наведенная поляризация на частоте световой волны, величина которой пропорциональна квадрату напряженности постоянного поля. Таким образом, квадратичный электрооптический эффект можно также отнести к семейству нелинейно – оптических эффектов.

Следует отметить, что в среде с квадратичной нелинейностью при двухчастотном воздействии возможно наблюдать нелинейно – оптические эффекты, характерные для кубично – нелинейной среды. Действительно, если ω2 = 2ω1 , то среди составляющих нелинейной поляризации мы находим слагаемое

c( 2 ) E01E02 cos[( w1 - w2 )t - ( k1 - k2 )z ] = c( 2 ) E01E02 cos[( w1 )t - ( k1 - k2 )z ] .

Таким образом, для световой волны с частотой ω1 в рассмотренной ситуации появляется нелинейная добавка к показателю преломления, обусловленная наличием волны с частотой ω2 . Соответственно, в случае двухчастотного воздействия, в среде с квадратичной оптической нелинейностью могут наблюдаться эффекты пространственного самовоздействия световых пучков, характерные для среды с кубичной нелинейностью. Заметим, что при тех же условиях возникает составляющая нелинейной поляризации на частоте третьей гармоники волны с меньшей частотой: ω1 + ω2 = 3ω1 . Таким образом, в рассматриваемой ситуации квадратично – нелинейная среда ведет себя как среда и с квадратичной, и с кубичной нелинейностями.

180

8.2. Нелинейное волновое уравнение

При анализе нелинейно – оптических взаимодействий световых волн используют нелинейное волновое уравнение. Получим его из стандартных уравнений Максвелла для диэлектрической среды:

Правая часть нелинейного волнового уравнения зависит от нелинейной поляризации среды, которая приводит к изменению спектрального состава светового поля в среде, вследствие оптической нелинейности.

8.3. Распространение светового пучка в нелинейно – оптической среде

При анализе нелинейной поляризации, наводимой световым полем в среде с кубичной нелинейностью, мы выяснили, что возникает составляющая поляризации на частоте падающей световой волны, величина которой пропорциональна квадрату ампитуды светового поля. Это значит, что световое поле с неоднородным распределением интенсивности наводит в такой среде оптические неоднородности, которые, в свою очередь, могут изменять пространственную структуру светового поля. В этом случае говорят о пространственном самовоздействии светового поля или пучка. Рассмотрим основные особенности такого самовоздействия и некоторые его результаты.

где x и z – поперечная и продольная координаты. В данном случае предполагается, что размер пучка в направлении x значительно превышает длину волны света, а в направлении y его поле однородно. Соответственно,