Вычислительная математика

так как первое слагаемое в (3.5) обращается в ноль, и тогда ошибка будет равна

f (n 1) ( ) (x j ) . (n 1)!

По аналоги можно получить формулы численного дифференцирования для производных более высоких степеней.

Пример 3.1. Выведем формулы численного дифференцирования, полученные на основе дифференцирования формулы Лагранжа для следующей таблицы

Формула (3.7) дает выражение для 1-ой производной и имеет первый порядок точности.

Построим многочлен Лагранжа по трем узлам и его производную:

91

Вычислим значения первой производной по формуле (3.9) и остаточные члены по формуле (3.6) в узловых точках:

Итак, вычислив значения первой производной по трем узлам, получаем формулы с точность 2-го порядка. Увеличив число узлов на единицу, порядок точности формул для вычисления 1-ой производной также увеличится на единицу. То есть порядок точности формул для производных первого порядка на единицу меньше числа узлов. Отметим, что для вычисления L1 (0,5) потребовались значения функции в двух точках, при

этом порядок точности такой же, как для трех точек. Причиной этого является то, что L1 (0,5) вычисляется по формуле цен-

тральных разностей.

В случае численного дифференцирования при неравноотстоящих узлах можно воспользоваться также формулой Ньютона (2.24). Тогда, представив многочлен Ньютона в виде

92

Если первая производная в (3.11) оценивается по первому слагаемому, то она имеет первый порядок точности, если по первым двум слагаемым, то ее порядок точности будет равен 2 и т.д.

По аналогии можно вычислить и другие производные, например, численно оценить производную 2-го порядка можно по формуле

Пример 3.2. Таблица значений функции имеет вид:

Требуется найти аналитическое выражение для оценки второй производной функции. Таблица разделенных разностей для заданной функции имеет вид (см. п. 2.5):

Тогда выполнив расчеты по формуле (3.12) получим:

f(x) 2(6, 055 0, 036((x 0,1) (x 1,1) (x 1, 4)))

12, 297 0, 216x .

93

Остаточный член для этой формулы можно вычислить, продифференцировав формулу (3.5) по x .

3.2.Численное дифференцирование при равноотстоящих узлах

Вэтом случае в качестве аппроксимирующей функции(x) выбирается многочлен в зависимости от положения точки

x и значения переменной t , которая осуществляет связь с переменной x . В качестве интерполирующей функции можно выбрать один из интерполяционных многочленов, описанных в разделе 2.14.

Пусть точка x , в которой необходимо выполнить операцию численного дифференцирования находится в средине таблицы и

Дифференцируя по t левую и правую части равенства (3.13),

Рассмотрим задачу вычисления первой производной по формуле (3.14), в которой будут учитываться только первых два

94

слагаемых. Тогда для частного случая дифференцирования в точке xk (в этом случае t 0 ) получим:

Формула (3.17) получена в результате дифференцирования остаточного члена формулы Стирлинга и вычисления его в точке t 0 . В силу (3.17) погрешность метода численного дифференцирования имеет вид:

шага уменьшается. Расчетная формула вычисления первой про-

мую погрешность, возникающую из-за неточности исходных данных следующим образом:

Из (3.19) видно, что неустранимая погрешность с уменьшением шага возрастает. Если посмотреть на график полной погрешности (рис. 3.1)

95

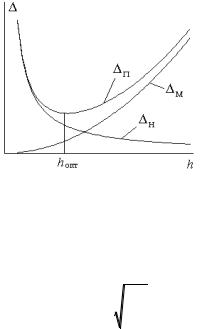
то можно сделать вывод, что существует оптимальный шаг hопт , обеспечивающий минимум полной погрешности.

Рис. 3.1 – Графики погрешностей

Найдем оптимальный шаг, из условия ( ) 0

h

и окончательно получаем

Отметим, что величину M3 можно оценить по формуле

Пример. 3.3. Требуется вычислить значение первой производной функции, которая задана в виде следующей таблице:

в точке x 1, 4 . Необходимо также оценить погрешность метода, неустранимую погрешность, полную погрешность, опти-

96

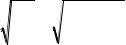
мальный шаг таблицы, считая, что табличные значения функции заданы с верными знаками.

При выполнении расчетов будем использовать конечные разности, приведенные в таблице

В этом случае для аппроксимации функции можно выбрать формулу Стирлинга при xk 1, 4 , где k 2 . Оценивать произ-

водную будем по первому слагаемому от производной формулы Стирлинга. В нашем примере h 0, 2, t 0 , погрешность таб-

личного значения функции равна 0, 0005 . Тогда в соответ-

ствии с формулами (3.18)-(3.22) получим следующие результаты:

97

Расчеты производной первого порядка показали, что производная вычисляется с погрешностью 0, 0367 . При этом минимальное значение полной погрешности может быть достигнуто для таблицы с шагом hопт 0, 066 .

Пусть точка x , в которой необходимо выполнить операцию численного дифференцирования находится вблизи начала таблицы. Тогда выберем формулу 1-ю формулу Ньютона :

.

Определим оптимальный шаг таблицы для случая, когда производная вычисляется в точке x0 . Тогда учитывая, что t 0 , по-

которая в нашем случае равна:

98

M3h2 4 3 h

выражение для hопт :

hопт 3 6 .

M3

Формула (3.25) имеет второй порядок точности, если производную вычислять только по первому слагаемому формулы (3.24), то формула будет иметь первый порядок точности. Минимизируя для этого случая полную погрешность

99

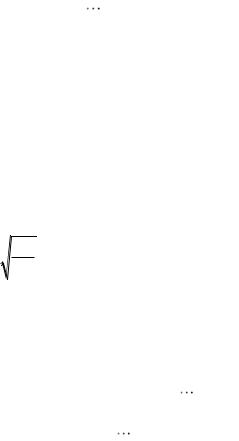
Тогда производная оценивается по формуле:

первая производная оценивается по первым двум слагаемым. В результате получим: