Электроника. Часть 1

51

Сравнивая с (1.43), замечаем, что поле при монополярной диффузии складывается из постоянной и демберовской составляющих. Строгое решение задачи о распределении носителей при монополярной диффузии встречает определенные трудности. Поэтому решим эту задачу для малых возмущений и в диффузионном приближении.

Величину возмущения принято характеризовать уровнем инжекции

δ = p ≈ n , p0 n0

т. е. отношением концентрации избыточных носителей к равновесной концентрации основных носителей. Малому возмущению соответствует неравенство δ << 1, т. е.

Это неравенство называют условием низкого уровня инжекции. Диффузионное приближение характеризуется тем, что в уравнении непрерывности пренебрегают составляющими, связанными с напряженностью поля. Стационарный и нестационарный режимы можно записать в виде:

Величина L определяется выражением

L = Dτ.

L имеет размерность длины и носит название средней диффузионной длины или средней длины диффузии. Остановимся сначала на стационарном решении уравнения (1.46). Как известно, его решение является суммой двух экспонент:

где коэффициенты A1 и A2 определяются из граничных условий

x = 0, x = w и принципа физической реализуемости. На бесконечно большем расстоянии от границы инжекции величина избыточной

52

концентрации должна стремиться к нулю в результате рекомбинации инжектированных носителей. Первый член уравнения

т. е. избыточные концентрации спадают по экспоненте. Это один из характерных случаев в теории полупроводниковых приборов.

Из выражения (1.49) следует, что диффузионная длина есть то расстояние, на котором концентрация диффундирующих носителей (при их экспоненциальном распределении) уменьша-

ется в е раз. На участке длиной (3—4)L концентрация уменьшается в 20—50 раз, т. е. становится пренебрежимо малой по сравнению с исходным значением. В заключение следует отметить, что материал первой главы является фундаментом, на котором базируются последующие разделы.

Таблица 1.1 — Основные параметры некоторых полупроводников

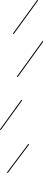
54

Таблица 1.2 — Основные физические константы, используемые в

теории полупроводников

Вопросы для самопроверки

1.Какие типы полупроводников Вы знаете?

2.Для каких целей вводятся примеси?

3.Почему примеси не образуют зон?

4.Объясните физический смысл потенциала Ферми и уровни его залегания в различных типах полупроводниковых материалов.

5.Объясните физический смысл температурного потенциа-

ла ϕT .

6.Что такое эффективная плотность состояний в зонах про-

водимости и валентной?

7. От каких параметров зависят концентрации p и n в собственном полупроводнике?

8.Что такое электростатический потенциал полупроводника?

9.Дайте определение понятию «химический потенциал»

ичто означает условие gradϕF = const ?

10.Какие полупроводники относятся к невырожденным?

11.Запишите потенциалы Ферми для дырочного и электронного полупроводников, если полупроводники невырожденные.

55

12.Где залегают уровни Ферми в дырочном, электронном

исобственном полупроводниках?

13.Запишите уравнение нейтральности. В чем его физический смысл?

14.В типичном электронном полупроводнике уровень Фер-

ипочему подвижность с повышением температуры падает?

16.Запишите формулы удельной проводимости для собственного, электронного и дырочного полупроводников. Нарисуйте графики зависимости удельной проводимости от температуры.

17.Что означает понятие «время жизни носителей» и почему с увеличением концентраций доноров или акцепторов время жизни падает?

18.Почему время жизни с повышением температуры растёт.

19.От каких параметров зависят диффузионные и дрейфовые токи в полупроводнике?

20.Объясните, что такое диэлектрическая релаксация в полупроводниках и связана ли она с уравнением нейтральности?

21.Принципиальное отличие неоднородных полупроводников от однородных?

22.Объясните основные процессы при биполярной диффу-

зии.

23.Объясните физическую сущность демберовского поля

инапряжённости.

24.В чем сходство и принципиальное отличие между монополярной и биполярной диффузиями?

25.Выведите формулу для избыточной концентрации носителей при монополярной диффузии.

26.Что означает диффузионная длина L?

56

2 ПОЛУПРОВОДНИКОВЫЕ ДИОДЫ

2.1 Введение

Полупроводниковый диод представляет собой комбинацию двух полупроводниковых слоев с различными типами проводимости (рис. 2.1). Такая комбинация обладает способностью гораздо лучше пропускать ток в одном направлении (от слоя p

к слою n ) и гораздо хуже в другом. Полярность напряжения, соответствующая большим токам, называется прямой, а соответствующая меньшим токам — обратной. Обычно пользуются терминами «прямое и обратное напряжение» (смещение), «прямой и обратный токи».

p-pn–nпереход-

p n

а

I

б

Рис. 2.1 — Плоскостной диод:

а — упрощенная структура; б — условное графическое обозначение

На рис. 2.1, б показаны символическое изображение диода, направление прямого тока и полярность прямого напряжения. Вентильное свойство диода является следствием ярко выраженной внутренней неоднородности структуры. Ступенчатая неоднородность даже в полупроводниках с одним типом проводимости сопровождается нарушением закона Ома в связи с образованием объемных зарядов и потенциального барьера. В данном случае, когда слои разнотипные, нелинейность, естественно, оказывается еще сильнее. Несмотря на кажущуюся простоту, диод

57

является сложным прибором, так как имеет много областей, обладающих различными физическими свойствами.

1.Области, прилегающие к границам металл-полупровод- ник. Металл необходим для создания выводов.

2.Области, прилегающие к границе (металлургическая граница), образованной двумя полупроводниковыми материалами p и n.

3.Области полупроводников вдали от металлургической границы.

Поверхность, по которой контактируют слои р и n, называется металлургической границей, а прилегающие к ней области объемных (или пространственных) зарядов — электроннодырочным переходом или р-n переходом. Два других внешних контакта в диоде должны быть не выпрямляющие: поэтому их называют омическими контактами.

Принципыполученияомическихконтактоврассмотримпозже. Плоскостными диодами и соответственно плоскостными переходами называют такие диоды и переходы, у которых граница между слоями плоская, а площади обоих слоев одинаковы. Эти условия не всегда соблюдаются на практике, но соблюдение этих условий облегчает анализ и в то же время позволяет получить правильное представление о процессах в реальном диоде

иего характеристиках. Диоды — самостоятельный, весьма обширный класс полупроводниковых приборов. В то же время диод как простейший прибор с одним р-n переходом является основой многопереходных приборов — транзисторов и других. Мы изучим диоды именно с этой точки зрения.

В общих чертах процессы в полупроводниковом диоде можно охарактеризовать следующим образом. В отсутствие внешнего напряжения имеет место больцмановское равновесие: вблизи металлургической границы, где сконцентрированы объемные заряды и связанное с ними поле, диффузионные и дрейфовые потоки носителей уравновешены и результирующего тока нет. Полярность прямого напряжения способствует «выталкиванию» дырок из р-слоя в n-слой и электронов в обратном направлении. В результате повышается концентрация дырок в n-слое

иконцентрация электронов в р-слое, т. е. имеет место инжекция неосновных носителей в обоих слоях диода. Инжектированные носители диффундируют в глубь слоев, и эта монополярная

58

диффузия сопровождается протеканием прямого тока. Полярность обратного напряжения способствует «выталкиванию» дырок из n-слоя и электронов из p-слоя в область перехода, т. е. имеет место экстракция неосновных носителей и протекает соответствующий обратный ток.

Диффузионный ток определяется граничной величиной избыточной концентрации неосновных носителей. Поскольку при экстракции модуль избыточной концентрации не может превышать весьма малого значения равновесной концентрации, а при инжекции такого ограничения нет, прямой ток оказывается намного больше обратного, что и является основой вентильных свойств диода.

2.2 Электронно-дырочный переход

Плоскостной диод состоит из электронно-дырочного перехода, двух нейтральных (или квазинейтральных) слоев и омических контактов. Поскольку процессы в нейтральных полупроводниках были детально изучены в первой главе, следует, прежде всего, рассмотреть процессы в р-n переходе и учесть возможное влияние нейтральных областей на характеристики и параметры диодов.

Классификация р-n переходов

Прежде всего, заметим, что p-n переход нельзя осуществить

путем простого соприкосновения двух разнородных полупроводниковых пластинок, так как при этом неизбежен промежуточный (хотя бы и очень тонкий) слой воздуха или поверхностных пленок. Настоящий переход получается в единой пластинке полупроводника, в которой тем или иным способом получена достаточно резкая граница между слоями р и n. Резкость границы играет принципиальную роль для образования перехода, так как нерезкая граница приводит к образованию плавного перехода, а как показывает теория, такой переход не обладает теми вентильными свойствами, которые требуются для работы полупроводниковых диодов и транзисторов.

59

Понятие резкости формулируется следующим образом: граница между слоями является резкой, если градиент концентрации примеси (считающийся постоянным в пределах перехода) удовлетворяет неравенству

длина в собственном полупроводнике.

Nа

Nд

x

0

ni

Рис. 2.2 — Распределение полных и эффективных концентраций примеси вблизи металлургической границы плавного перехода

Переходы, в которых имеется скачкообразное изменение dx =∞), будем называть сту-

пенчатыми. Они представляют собой предельный случай класса резких переходов, в которых градиент концентрации примесей конечен, но удовлетворяет неравенству (2.1). На практике ступенчатые переходы являются, конечно, известным приближением. Однако они хорошо отражают свойства многих реальных р-n

60

структур и, кроме того, оказываются проще для анализа. Поэтому ниже им будет уделено главное внимание.

Контакты, в которых условие (2.1) не соблюдается, не называют переходами, а относят к неоднородным полупроводникам. По соотношению концентраций основных носителей в слоях р иn переходы делятся на симметричные и несимметричные. В симметричных переходах имеет место соотношение pp ≈ nn , т. е. концен-

трации основных носителей в обоих слоях почтиодинаковы. Такие переходы используются сравнительно редко и не яв-

ляются типичными. Гораздо большее распространение имеют несимметричные переходы, в которых выполняется неравенство

и концентрации различаются в несколько раз. Именно такие переходы будут анализироваться в дальнейшем, причем для определенности считаем, что слой р более низкоомный, чем слои n,

т. е. p >n .

Полученные выводы легко использовать при обратном соотношении концентраций. В случае резкой асимметрии, когда концентрации основных носителей различаются более чем на порядок, переходы называют односторонними и обычно обознача-

ют символами ( n-p+ или n+ -p ). Иногда, чтобы отличить несимметричные переходы от односторонних, используют для первых обозначения p+ -n (или n+ -p ), а для вторых p++-n (или n++-p ).

Структура р-n перехода. Концентрации примесей и свободных носителей в каждом из слоев диода показаны на рис. 2.3, а, причем для наглядности разница в концентрациях pp и nn

принята гораздо меньшей, чем это имеется в действительности. Поскольку концентрация дырок в слое р значительно боль-

ше, чем в слое n, после соединения полупроводников часть дырок диффундирует из слоя р в слой n. При этом в слое n вблизи металлургической границы окажутся избыточные дырки. Вследствие диэлектрической релаксации избыточный заряд дырок будет компенсирован электронами полупроводника n-типа. Наличие разности концентраций дырок в полупроводнике n приведет к образованию разности химических потенциалов и к возникновению диффузии.