Финансовые вычисления

12 РАЗДЕЛ I. Общая часть

Решение:

По формуле I = P nr при P = 200; n = 3; r = 0,15

I = 200 3 0,15 = 90

Сумма процентных денег равна 90 тыс. руб.

F = 200 +90 = 290

Возвращаемая сумма равна 290 тыс. руб.

.. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Вформуле (1.1) размерности r и n должны быть согласованы: если период начисления процентов измеряется в годах, то задается годовая ставка.

Впрактической деятельности ссуды часто выдают на период, меньший одного года, тогда в расчетах используют промежуточную процентную ставку, которая равна доле годовой ставки, пропорциональной доле временного интервала в году:

где t — продолжительность финансовой операции, дней; T — количество дней в году; r~T — промежуточная процентная ставка.

День выдачи и день погашения ссуды считаются за один день, а продолжительность периода предоставления ссуды может определяться двумя способами:

1)точный способ, в котором используются специальные таблицы (прил. Б), где каждому дню года соответствует свой порядковый номер. Точное число дней ссуды определяется следующим образом:

2)приближенный способ, в котором рассчитывается приблизительное число дней ссуды, когда продолжительность полного месяца принимается равной 30 дням.

Результат финансовой операции может определяться тремя различными способами:

1)обыкновенный процент с точным числом дней ссуды (T = 360 дней);

2)обыкновенный процент с приближенным числом дней ссуды (T = 360 дней);

3)точный процент с точным числом дней ссуды. Точный процент получают, когда за временную базу берут фактическое число дней в году (365 или 366), в квартале (от 89 до 92), в месяце (от 28 до 31) и точное число дней ссуды.

Ссуда на 3000 долл. предоставлена 16 января. Условия погашения: через 9 месяцев под 25% годовых (год не високосный). Рассчитайте сумму к погашению при различных способах начисления процентов.

Решение:

Для определения наращения капитала по простой ставке ссудного процента воспользуемся формулой (1.2):

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Для определения современной стоимости получаемой в будущем суммы используется метод математического дисконтирования. Операция дисконтирования производится по формуле:

Финансовое соглашение может предусматривать не только постоянную процентную ставку на весь период, но и устанавливать изменяющуюся во времени (переменную) ставку. Например, наличие инфляции вынуждает постоянно изменять процентную ставку.

Если на последовательных интервалах начисления, продолжительность которых составляет n1, n2, . . . , применяются соответствующие им ставки процентов r1, r2, . . . , то наращенная сумма составит:

•в конце первого интервала F1 = r1 n1;

•в конце второго интервала F2 = F1 r2 n2 = P (1 +n1 r1 +n2 r2). При N интервалах начисления наращенная сумма составит

14 РАЗДЕЛ I. Общая часть

Обозначим

i=1

тогда формула (1.4) примет вид F = P (1 +nr¯), т. е на весь период можно установить среднюю ставку r¯ и для вычисления наращенной суммы использовать формулу (1.1).

1.2.2 Простые учетные ставки

При антисипативном способе начисления процентов сумма получаемого дохода рассчитывается исходя из суммы, получаемой по прошествии интервала начисления (то есть из наращенной суммы). Эта сумма и считается величиной получаемого кредита (ссуды). Так как проценты в данном случае начисляются в начале каждого интервала начисления, заемщик получает сумму кредита за вычетом процентных денег. Такая операция называется дисконтированием по учетной ставке или коммерческим (банковским) учетом.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Дисконт — это доход, полученный по учетной ставке, то есть разница между размером предоставляемого кредита и непосредственно выдаваемой суммой.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Введем обозначения для нижеприведенных формул: d — простая годовая учетная ставка;

P — сумма, получаемая заемщиком;

F — сумма, подлежащая возврату.

Для расчета показателей, используемых при предоставлении кредита, используются следующие формулы:

а) для определения суммы, получаемой заемщиком:

• в конце первого интервала: P1 = F −d F ;

• в конце второго интервала: P2 = F −d F = F (1 −2 d);

• на весь период кредитования:

Банковский учет применяется в операциях по учету векселей. Банк покупает вексель у владельца до наступления срока оплаты по цене, меньшей той суммы, которая должна быть выплачена по векселю в конце срока (меньшей номинальной стоимости векселя).

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Сумма, которую получает векселедержатель при досрочном учете векселя, называется дисконтированной величиной векселя.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Операция банковского дисконтирования по учетной ставке имеет смысл, если

(1 −nd) > 0 nd < 1 n < 1~d.

За вексель, учтенный за 5 лет до срока погашения по учетной ставке 14% годовых, заплачено 4000 руб. Определить номинальную стоимость векселя.

Решение:

По формуле (1.8) получаем F = 400~(1 −0,14 5) = 13333 руб.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Математическое дисконтирование выгоднее для векселедержателя, а банковское — для банка. В таблице 1.1 приведены значения дисконтированной суммы по ссудной и учетной ставках 10% годовых при F = 100 ед. Значения дисконтированной суммы вычисляются по соответствующим формулам:

Pr = F ~(1 +nr), Pd = F (1 −nd).

Таблица 1.1 – Дисконтирование по ссудной и учетной ставках

16 РАЗДЕЛ I. Общая часть

Простая учетная ставка обеспечивает более быстрый рост капитала, чем такая же по величине процентная ставка. В таблице 1.2 приведены значения наращенной суммы по ссудной и учетной ставках 10% годовых при P = 100 ед. Значения наращенной суммы вычисляются по соответствующим формулам:

Fr = P (1 +nr), Fd = P ~(1 −nd).

Таблица 1.2 – Наращение по ссудной и учетной ставках

1.3 Сложные ставки

1.3.1 Сложные ссудные ставки

Для пояснения разницы между простыми и сложными процентами рассмотрим ситуацию: клиент положил в банк на несколько лет сумму, равную P , под простые проценты по ставке r, причем счет можно закрыть в любое время. Если клиент закроет счет через 2 года, то на руки он получит сумму F 1 = P (1 +2r). Но клиент может поступить таким образом: через год закрыть счет, получить на руки сумму F = P (1 + r), а затем положить эту сумму еще раз на год, осуществив операцию

реинвестирования. Такое действие позволит ему в конце второго года получить

F 2 = F (1 +r) = P (1 +r)(1 +r) = P (1 +r)2.

Величина F 2 > F 1 на величину P r2 = (P r)r, которая представляет собой проценты на начисленные проценты. Ясно, что клиенту выгодно каждый раз переоформлять счет, поэтому с целью предотвращения такого рода действий банки

внекоторых случаях используют сложные проценты.

Всхеме сложных процентов очередной годовой доход исчисляется не с исходной, а с общей суммы, включающей начисленные проценты. Происходит капитализация процентов, т. е. база, с которой они начисляются, все время возрастает. Размер возвращаемой суммы рассчитывается по формулам:

•через 1 год: F1 = P +P r = P (1 +r);

•через 2 года: F2 = F1 +F1 r = F1 (1 +r) = P (1 +r)2;

. . .

•через n лет:

=P (1 +r)n. (1.12)n

Величина начисленных процентов составит: I = F −P = P (1 +r)n −(1 +nr) . Часть из них получена за счет начисления процентов на основную часть долга:

P nr.

Оставшаяся часть получена за счет начисления процентов на проценты:

Ip = P (1 +r)n −1 −P nr = P (1 +r)n −(1 +nr) .

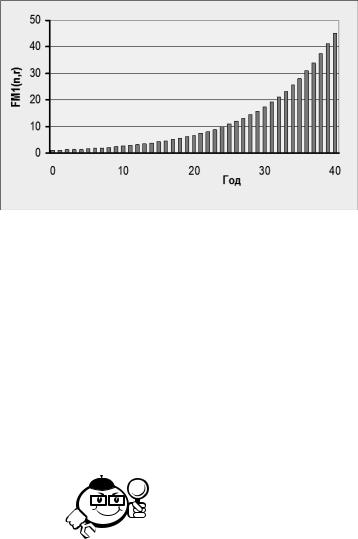
Вычислить наращенную сумму для заданных процентной ставки и количества лет можно при помощи финансовых таблиц, в которых протабулировано значение мультиплицирующего множителя (см. прил. А). Мультиплицирующий множитель для cложной процентной ставки равен (1 +r)n и имеет специальное обозначение

F M1(r, n).

На рис. 1.2 приведен график зависимости множителя наращения от срока финансовой операции при r = 10%.

Рис. 1.2 – Зависимость множителя наращения от срока финансовой операции

Для примерного расчета количества лет, необходимых для увеличения денежной суммы в два раза при условии, что весь процент остается на депозите, применяется правило 72, использующее число 72. Чтобы рассчитать этот срок, нужно разделить 72 на ставку процента, выраженную целым числом. Это правило достаточно хорошо срабатывает при ставке от 3 до 18% ( 72~3 = 24 года; 72~4 = 18 лет;

72~12 = 6 лет).

Правило 72 действует также и в обратном направлении. Если известно, что за шесть лет 10000 руб. превратились в 20000 руб., то сложная годовая ставка составляет примерно 12%. Если же 10000 руб. удвоились за 10 лет, то ставка равна примерно 7,2%.

Годовая ставка сложных процентов равна 8%. Через сколько лет начальная сумма удвоится?

Решение:

Необходимо решить неравенство

(1 +0,8) 2; n Ln(2)~Ln(1,08); n 9.

Решая пример по правилу 72, получим: 72~8 = 9.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Определить приведенную стоимость для заданных процентной ставки и количества лет можно по формуле

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Величина 1~(1 +r)n называется коэффициентом дисконтирования или дисконтирующим множителем и обозначается F M2(r, n). Его значение также занесено в финансовые таблицы (см. прил. А).

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Наращенная сумма при различных ставках сложных процентов на разных интервалах исчисления (n1, n2, . . . — продолжительность интервалов начисления в годах; r1, r2, . . . — годовые ставки процентов, соответствующие этим интервалам)

Вслучае получения краткосрочных ссуд со сроком погашения до одного года

вкачестве показателя продолжительности срока ссуды n берется величина, равная удельному весу длины подпериода (день, месяц, квартал, полугодие) в общем периоде (год). Длина различных подпериодов в расчетах округляется: месяц — 30 дней, квартал — 90 дней, полугодие — 180 дней, год — 360 дней.

Рассчитать наращенную сумму с исходной суммы 2000 руб. при помещении ее в банк на условиях начисления простых и сложных процентов с годовой ставкой 20% и периодами наращения: 90 дней, 180 дней, 1 год, 5 лет, 10 лет.

Решение:

Результаты расчета представлены в таблице 1.3.

Таким образом, если денежные средства размещены в банке на срок менее 1 года, то выгоднее использовать схему простых процентов; при размещении средств на срок более 1 года выгоднее схема сложных процентов.

Вобщем виде можно записать:

•(1 +nr) > (1 +r)n, при n > года;

•(1 +nr) < (1 +r)n, при n < года.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Таблица 1.3

Часто на практике оговаривается величина годового процента и количество периодов начисления процентов. Тогда расчет наращенной суммы ведется по формуле сложных процентов

где r — объявленная годовая ставка; m — количество начислений в году; n — количество лет.

В банк вложены деньги в сумме 5000 руб. на 2 года с полугодовым начислением процентов по ставке 20% годовых. Определить наращенную сумму при полугодовом и поквартальном начислении сложных процентов.

Решение:

При полугодовом начислении процентов наращение происходит 4 раза по ставке 10%, а наращенная сумма составит:

F = 5000 1,4641 = 7320,5 руб.

Если проценты начисляются ежеквартально, то наращение происходит 8 раз по ставке 5%, а наращенная сумма составит:

F = 5000 1,4774 = 7387,3 руб.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Таким образом, чем чаще идет начисление по схеме сложных процентов, тем больше накопленная сумма. Заметим, что при начислениях по схеме простых процентов частота начислений не играет роли, так как наращение всегда происходит от исходной суммы.

Если контракт заключается на период, не равный целому числу лет, проценты могут начисляться двумя способами:

где f — дробная часть года; w — целое число лет;

2)по смешанной схеме (сложные проценты для целого числа лет и простые проценты для дробной части года):

Так как f < 1, то (1 +f r) > (1 +r), поэтому наращенная сумма будет больше при использовании смешанной схемы.

1.3.2 Сложная учетная ставка

При использовании сложной годовой учетной ставки для определения параметров финансовой сделки используем следующие формулы:

1)для определения суммы, получаемой заемщиком:

•в конце первого интервала: P1 = F −d F = F (1 −d);

•в конце второго интервала: P2 = P1 −P1 d = F (1 −d)−F (1 −d) d =

=F (1 −d)2;

•через n лет:

=F (1 −d)n; (1.18)n

Учет по сложной ставке может выполняться при любых ставках и сроках, т. к. всегда верно: (1 −d)n > 0.

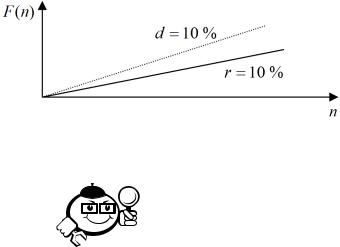
Наращение сумм по сложной учетной ставке и сложной ссудной ставке происходит с разной скоростью (рис. 1.3): скорость выше при применении сложной учетной ставки.

Рис. 1.3 – Наращенная сумма при начислении сложных процентов

Первоначальная сумма долга равняется 10 млн руб. Определить величину наращенной суммы при использовании декурсивного и антисипативного начисления процентов, если годовая ставка равна 20% годовых, срок начисления процентов — 3 года.