Физические основы вакуумной и плазменной электроники

Главной задачей электростатики является нахождение величины вектора напряженности электрического поля E в различных электрических устройствах (кабелях, конденсаторах и др.). Расчеты сами по себе не просты, а разнообразие диэлектриков и проводников еще более усложняет эту работу.

Рисунок 2.6

Для упрощения расчетов была введена новая векторная вели-

чина – вектор электрического смещения (электрическая индукция)

D 0 E.

Нормальная составляющая вектора D остается неизменной при переходе из одной диэлектрической среды в другую. Это облегчает расчет полей. Зная D и , можно определить напряженность:

E D .

0

Распишем вектор D:

D 0 E 1 0 E 0 E 0 E 0 E P.

Вектор D есть сумма двух векторов различной природы. Вектор E – это главная характеристика поля, напряженность. Вектор P – это вектор поляризации, определяющий электрическое состояние вещества в электрическом поле. В СИ он измеряется в кулонах на метр квадратный (Кл/м2).

Для точечного заряда, например, получается

D 4 qr2 .

Для вектора электрической индукции D имеет место принцип суперпозиции, как и для вектора напряженности E.

– 41 –

Поток вектора электрического смещения

Аналогично потоку вектора E можно ввести понятие потока вектора D:

ФE EndS , ФD Dn dS .

S S

В однородном электрическом поле поток вектора электрической индукции определяется выражением

ФD DS cos Dn S.

Как известно, теорема Остроградского – Гаусса для вектора E имеет вид

E dS qi .

S 0

Так как E D , то теорема Остроградского – Гаусса для век-

0

тора D запишется

D dS qi .

S

Отсюда становится ясным смысл введения вектора D.

Поток вектора электрического смещения D через любую замкнутую поверхность определяется только свободными зарядами, а не всеми зарядами внутри объема, ограниченного данной поверхностью (рисунок 2.7).

Рисунок 2.7

– 42 –

Это позволяет не рассматривать связанные (поляризационные) заряды, влияющие на величину вектора напряженности E, что упрощает решение многих задач.

Рассмотрим поведение векторов E и D на границе раздела двух бесконечно протяженных однородных изотропных диэлектриков. Пусть на границе раздела диэлектриков находится сторонний поверхностный заряд. Искомые условия можно получить с помощью двух теорем: теоремы о циркуляции вектора E и теоремы Остроградского – Гаусса для вектора D:

Условие для вектора E:

E1 E2 .

Таким образом, тангенциальная составляющая вектора E оказывается одинаковой по обе стороны границы раздела, т.е. не претерпевает скачка.

Условие для вектора D:

D1n D2n.

В этом случае нормальная составляющая вектора D скачка не испытывает, она оказывается одинаковой по разные стороны границы раздела.

Таким образом, если на границе раздела двух однородных изотропных диэлектриков нет сторонних зарядов, то при переходе этой границы составляющие E и Dn изменяются непрерывно, без скач-

ка. А компоненты En и D претерпевают скачок.

Пусть 2 > 1. На границе раздела возникают поляризационные заряды с поверхностной плотностью 1 и 2 (рисунок 2.8).

Дополнительное электрическое поле, создаваемое этими зарядами ( E ), перпендикулярно поверхности раздела. Поэтому нормальные составляющие напряженности электрического поля будут изменяться, а тангенциальные – нет:

– 43 –

Следовательно, будет происходить изменение направления вектора E при переходе из одной диэлектрической среды в другую (рисунок 2.9).

Рассмотрим теперь, как будет вести себя вектор электрической индукции на границе раздела двух диэлектриков (рисунок 2.10).

Рисунок 2.8

– 44 –

Таким образом, еще раз показали, что нормальная составляющая вектора не изменяется при переходе из одной диэлектрической среды в другую:

Dn1 Dn2 , D 1 1 , D 2 2

2 1: D 1 D 2 (рисунок 2.11).

Рисунок 2.11

Вектор D преломляется в ту же сторону и под тем же углом, что и вектор E:

– 45 –

В установившемся состоянии:

1) во всех точках внутри проводника напряженность электростатического поля равна нулю (E = 0), а во всех точках его поверхности E = En ( E = 0);

2) весь объем проводника, находящегося в электростатическом поле, эквипотенциален. Действительно, в любой точке внутри проводника

d E 0, тоесть const; dl

3) поверхность проводника тоже эквипотенциальна. Для любой линии на поверхности проводника можно записать

d E 0, тоесть пов const; dl

4) в заряженном проводнике не скомпенсированные заряды располагаются только на поверхности проводника. Их расталкивают кулоновские силы.

Напряженность поля вблизи поверхности заряженного проводника прямо пропорциональна поверхностной плотности зарядов :

En Dn .

0 0

Электроемкость

Сообщенный проводнику заряд распределяется по его поверхности так, чтобы напряженность поля внутри проводника была равна нулю. Такое распределение заряда является единственно возможным. Если проводнику, уже несущему заряд q, сообщить еще заряд, то второй заряд должен распределиться по проводнику точно таким же образом, как и первый заряд, т.е. чтобы внутри проводника E = 0. Все это справедливо для уединенного проводника. Если вблизи находятся другие тела, то появляются индуцированные заряды и они могут исказить идеальную картину.

Итак, различные по величине заряды распределяются на уединенном проводнике подобным образом (отношение плотностей заряда в двух произвольных точках поверхности проводника при любом заряде будет одним и тем же).

– 47 –

Отсюда вытекает, что потенциал уединенного проводника пропорционален находящемуся на нем заряду:

q C .

Коэффициент пропорциональности между потенциалом и зарядом называется электроемкостью:

C q .

Емкость численно равна заряду, сообщение которого проводнику вызывает повышение его потенциала на единицу.

В СИ емкость измеряется в фарадах: 1 Ф 11КлВ .

Емкость уединенного шара

C 4 0R.

Емкость 1 Ф очень большая величина – это емкость уединенного шара радиусом 9 109 м (для сравнения: радиус Земли равен

6,378 106 м).

Уединенные проводники обладают небольшой электроемкостью. Вместе с тем необходимы устройства, которые при небольших размерах конденсируют большое количество заряда. Такие устройства называют конденсаторами. В них используется явление возрастания емкости проводника при приближении к нему других тел. Индуцированные заряды одного тела подтягивают к себе заряды другого тела и потенциал проводника уменьшается.

Конденсатор – это два проводника, расположенных близко друг от друга, которые называются обкладками. Чтобы внешние тела не оказывали влияние на емкость конденсаторов, обкладкам придают такую форму и так располагают друг относительно друга, чтобы поле, создаваемое зарядом конденсатора, было сосредоточено внутри конденсатора. Этому условию удовлетворяют две пластины, два коаксиальных (имеющих одну ось) цилиндра, две концентрические сферы (имеющие общий центр) (рисунок 2.13).

Соответственно бывают плоские, цилиндрические и сферические конденсаторы. Так как электрическое поле заключено внутри конденсатора, то и линии электрического смещения начинаются на

– 48 –

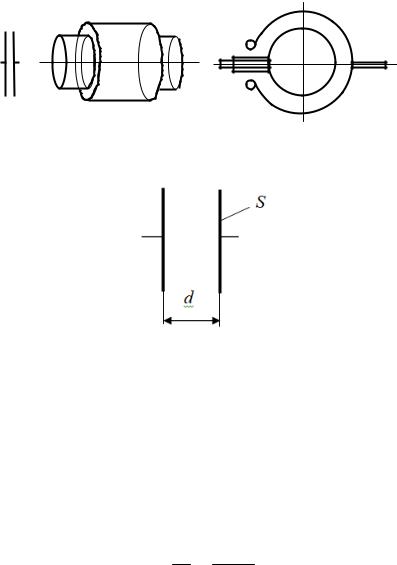
положительной обкладке и заканчиваются на отрицательной обкладке, никуда не исчезая. Следовательно, заряды на обкладках противоположны по знаку и одинаковы по величине (рисунок 2.14).

Рисунок 2.13

Рисунок 2.14

Емкость конденсатора определяется выражением

где U – напряжение между обкладками. Емкость плоского конденсатора

C Uq d0S .

Помимо емкости, каждый конденсатор характеризуется рабочим напряжением Uраб , для высоковольтных конденсаторов в качестве характеристики используется пробивное напряжение Uпр (максимально допустимое напряжение).

При параллельном соединении конденсаторов общим (одинаковым) является напряжение U (рисунок 2.15).

При этом суммарная емкость конденсаторов

N

CCi .

i1

– 49 –

При последовательном соединении конденсаторов их крайние обкладки заряжаются разноименными зарядами q (рисунок 2.16). Вследствие электростатической индукции на всех промежуточных пластинах наводятся заряды, также численно равные q. Следовательно, одинаковым для конденсатора является заряд q.

При последовательном соединении конденсаторов общая емкость рассчитывается по формуле

Если необходимо увеличить емкость, то конденсаторы соединяют в батарею параллельно. Если необходимо повысить рабочее напряжение, конденсаторы соединяют в батарею последовательно, но при этом емкость уменьшается.

Энергия заряженного проводника

Заряд q, находящийся на некотором проводнике, можно рассматривать как систему точечных зарядов qi. Ранее мы получили выражение для энергии взаимодействия системы зарядов

WП 1 N i qi ,

2 i 1

где i – потенциал, создаваемый всеми зарядами, кроме заряда qi в

той точке, где он помещается.

Поверхность проводника является эквипотенциальной. Поэтому потенциалы тех точек, в которых находятся точечные заряды qi ,

– 50 –