Учебное пособие «Микросхемотехника Аналоговая микросхемотехника»

6. аМЪВ„р‡О¸М˚В ‡М‡ОУ„У‚˚В ФВрВПМУКЛЪВОЛ

6.1. лФУТУ·˚ ФУТЪрУВМЛfl ЛМЪВ„р‡О¸М˚ı ‡М‡ОУ„У‚˚ı ЫТЪрУИТЪ‚ ЫПМУКВМЛfl

Аналоговый перемножитель является активным устройством, выходное напряжение которого пропорционально произведению двух входных. С использованием обозначений, приведенных на рисунке 6.1, выполняемую им функцию можно записать

где K — масштабный коэффициент.

Рисунок 6.1 — Аналоговый перемножитель: а — обозначение; б — эквивалентная схема

От масштабного коэффициента зависит единичное напряжение, при котором U X1UY1 UZ1.

– 211 –

Идеальный перемножитель имеет бесконечные полные входные сопротивления, нулевое выходное сопротивление и частотнонезависимый масштабный коэффициент, который не зависит ни от U X , ни от UY . Его выходное напряжение равно нулю, когда хотя

бы одно из входных напряжений равно нулю. Другими словами, напряжения смещения, дрейфа и шума равны нулю.

Реальные перемножители являются только приближениями идеального устройства и имеют конечные напряжения смещения, дрейфа и шума. Для того чтобы вызываемые ими погрешности имели приемлемый уровень, единичные напряжения должны выбираться довольно большими, обычно от 1 до 10 В.

Из множества известных способов построения интегральных аналоговых устройств умножения наиболее пригодными являются следующие.

Логарифмическое суммирование (рисунок 6.2,а). Реализация этого метода основана на использовании соотношения

X kx A, Y kyt и Z kzT,

где А — амплитуда импульса; t — его длительность; Т — площадь импульса, то

Z kz / kxky XY ,

Управляемое распределение тока (рисунок 6.2,в). Суть этого метода заключается в том, что выходной дифференциальный ток управляемого линейного делителя тока пропорционален произведению токов I1 и I2 . Из рисунка 6.2,в следует, что выходные токи

и их разность соответственно можно записать:

– 212 –

Основной недостаток первого метода заключается в том, что напряжения U x и U y должны быть положительными и не могут

уменьшаться до нуля. Второй метод обеспечивает высокую точность, но непригоден для применения на высоких частотах вследствие ограничений, обусловленных невысокой скоростью переключения. Управляемые делители тока хорошо работают и на высоких частотах.

6.2. мПМУКВМЛВ ФрЛ ФУПУ˘Л ЫФр‡‚ОflВП˚ı М‡ФрflКВМЛВП ‰ВОЛЪВОВИ ЪУН‡

Простейший способ реализации управляемого напряжением делителя тока заключается в использовании симметричного дифференциального каскада, коллекторные токи которого определяются выражениями (6.4). Пусть Ux обозначает напряжение Uвх1 Uвх2 ,

– 213 –

Рисунок 6.3 — Управляемый напряжением делитель тока на основе симметричного дифференциального каскада

Считая, что коэффициенты усиления по току велики, то есть1, показанный на рисунке 6.3 параметр x можно записать

Для дифференциальных составляющих выходного тока и напряжения, которые пропорциональны параметру Z, можно записать следующие соотношения:

– 214 –

Из этих выражений видно, что параметр Z пропорционален

XY.

При использовании схемы, представленной на рисунке 6.3, необходимо найти компромисс между простотой и следующими ограничениями:

а) поскольку ток I0 I y не может быть отрицательным, дан-

ная схема является двухквадрантным перемножителем;

б) перемножитель является линейным по каналу I y , но нелинейным по каналу Ux вследствие нелинейности характеристики усилителя, поэтому Ux не должно превышать нескольких милли-

абсолютной температуры Т.

Первое ограничение можно устранить посредством применения четырехквадрантной схемы (рисунок 6.4), в которой применяются три управляемых напряжением делителя тока. Используя обозначения на этом рисунке, получаем

му гиперболическая функция может быть аппроксимирована линейной, получим

– 215 –

I0

UИП

Рисунок 6.4 — Четырехквадрантный перемножитель на основе дифференциального каскада

Схема имеет два недостатка.

Первый заключается в том, что масштабный коэффициент является квадратичной функцией температуры:

Второй состоит в том, что гиперболическая функция, связывающая токи и напряжения, обусловливает нелинейность характеристики по обоим входным сигналам. Следует отметить, что при

– 216 –

работе в составе переключающего перемножителя, когда дифференциальные каскады используются в качестве ограничителей, их гиперболическая характеристика является, скорее, преимуществом, чем недостатком.

При малых значениях Ux и U y нелинейность можно оценить

с помощью второго члена разложения в ряд гиперболической функции. Переписывая выражение (6.13) с учетом этого члена, получим

откуда можно найти относительную погрешность

Нелинейность является существенным ограничением в случае работы в режиме усиления сигналов постоянного тока. Например, пусть допустимая погрешность нелинейности будет равна 1 %.

Тогда значение U x2 U y2 не должно превышать 9 мВ, т.е. напряжения, сравнимого с напряжениями смещения и дрейфа.

6.3. мПМУКВМЛВ ФрЛ ФУПУ˘Л ЫФр‡‚ОflВП˚ı ЪУНУП ‰ВОЛЪВОВИ ЪУН‡

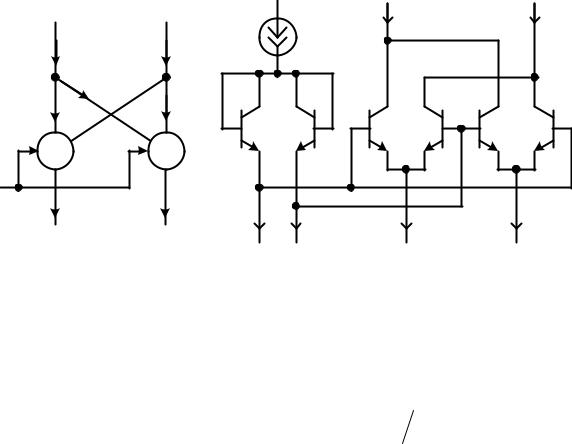
Простейший способ реализации управляемого током делителя тока иллюстрируется на рисунке 6.5, где два токовых зеркала объединены в симметричный дифференциальный каскад. Если транзисторы VT1–VT4 имеют значительное усиление ( 1) и пренебрежимо малое объемное сопротивление, уравнения для контуров, содержащих переходы база-эмиттер, можно записать в виде

– 217 –

Обозначая

UИП

Рисунок 6.5 — Управляемый током делитель тока на основе симметричного дифференциального каскада

и I1 I2 , которые пропорциональны параметрам X ,Y и Z .

– 218 –

Тогда

Если транзисторы VT1–VT4 имеют одинаковую геометрию, характер распределения примесей и температуру переходов, то1 и вышеприведенное выражение можно упростить:

Из выражения (6.21) видно, что характеристика линейна по отношению к обоим сигналам IX и IY . Более того, масштабный ко-

эффициент 1Iб не зависит от окружающей температуры. По-

этому данная схема имеет преимущество по сравнению с простой управляемой напряжением схемой, показанной на рисунке 6.3. Ее единственный недостаток заключается в том, что она является двухквадрантной, так как ток IX I0 не может быть отрицатель-

ным.

Один из возможных способов устранения такого ограничения показан на рисунке 6.6, где два управляемых током делителя тока образуют четырехквадрантное устройство умножения.

В этом случае

I1 I2 y1Ix1 1 y2 Ix2 y2Ix2 1 y1 Ix1

Из уравнений для контуров, содержащих переходы базаэмиттер транзисторов VT1–VT4 и VT1, VT2, VT5, VT6, имеем

– 219 –

При выводе выражения (6.23) было принято допущение, что VT1–VT6 являются транзисторами с большими коэффициентами усиления и пренебрежимо малыми объемными сопротивлениями.

Рисунок 6.6 — Четырехквадрантный перемножитель на основе управляемых током дифференциальных каскадов

Если они имеют одинаковую структуру и температуру переходов, то 1 2 1 и

чим IZ I X IY Iб .

В этом случае направление протекания тока IX может быть любым.

6.4. гЛМВИМ˚В ФрВУ·р‡БУ‚‡ЪВОЛ М‡ФрflКВМЛВ — ЪУН

Перемножитель, представленный на рисунке 6.6, имеет один недостаток: необходимость управления от источника тока может вызвать трудности при его применении. Поэтому целесообразно каждый вход дополнить линейным преобразователем напряжение – ток.

– 220 –