Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Материалы и элементы электронной техники. Часть 2

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

1.59 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1211 12 > Следующая >>>

	11	0	0	C13	0	0
ij	0	22	0	0	C23	0		33
	0	0	33	0	0	C33
	0	0					10.4	0	0
10.4	0	0					10.4	0	0
0	10.4	0	1010	10 6	10 1		0	10.4	0	103 H / м 2 .
0	0	107.1					0	0	107.1

Таким образом, деформация кристалла вдоль оси симметрии третьего порядка привела к возникновению одноосных упругих напряжений по трем взаимно перпендикулярным направлениям: Х1, Х2, Х3.

Задача 3. Определить упругость кристалла низкотемпературного
кварца в направлении единичного вектора			0) ,	если упругие
	n(1 2, 1 2,
постоянные кварца равны следующим		значениям	(в	ед. СГСЕ):

C11	86 1010 , C12	4.8 1010 , C13		10.4 1010 , C14 18.2			1010 ,
C33	107.1 1010 , C44	58.6 1010 , C66			40.5 1010 .
	Решение. Величина физического свойства четвертого ранга в

направлении единичного			вектора		n	вычисляется	как нормальная
составляющая тензора (см. Учебное пособие по курсу.)
		Cn	Cijkl	ni	n j	nk nl ,

представляющее собой сумму по всем четырем индексам. Поскольку по условию задачи n3 = 0, то индексы i, j, k, l могут принимать только значения 1

и 2. Следовательно в обозначениях Фохта будем иметь (см. Таблицу 4):

101

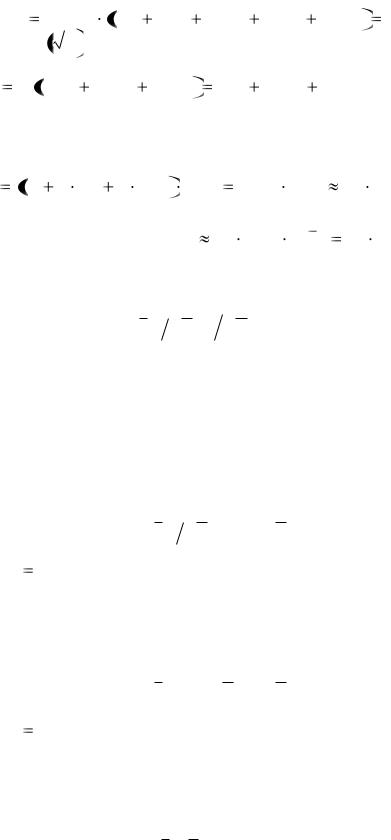
Cn			1		C11	C22	2C12	2C21	4C66

				2
			2	2
	1	2C 4C 4C					C 2C 2C .
		2C 4C 4C					C 2C 2C .
2			11		12	66	11	12	66
2

Подставив численные значения упругих постоянных, найдем (в ед. СГСЕ)

Cn 86 2 4.8 2 40.5	1010 176.6 1010	18. 1012 .
Переведем результат в систему СИ:	Cn 18. 1012 10 1	18. 1011 Н / м2 .

Такое значение упругой постоянной кристалла низкотемпературного кварца

следует ожидать в направлении n(1 2, 1 2, 0) .

19.3. ВАРИАНТЫ ЗАДАНИЙ ПО ОПРЕДЕЛЕНИЮ

ФИЗИЧЕСКИХ СВОЙСТВ, ОПИСЫВАЕМЫХ

ТЕНЗОРАМИ ЧЕТВЕРТОГО РАНГА

1. Определить упругость кристалла низкотемпературного кварца в направлении единичного вектора n(1 2, 0, 1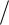2) . Форму матрицы упругих постоянных Cijkl Cmn взять из Таблицы 4, а значения упругих постоянных

-из задачи 2.

2.Определить упругость кристалла низкотемпературного кварца в

направлении единичного вектора n(0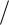, 12, 1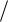2) . Форму матрицы упругих

постоянных Cijkl Cmn взять из Таблицы 4, а значения упругих постоянных

-из задачи 2.

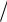3.Определить упругость кристалла низкотемпературного кварца в направлении единичного вектора n(32, 1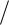2, 0) . Форму матрицы упругих

102

постоянных Cijkl Cmn взять из Таблицы 4, а значения упругих постоянных

- из задачи 2.

4. Определить упругость кристалла низкотемпературного кварца в направлении единичного вектора n(3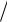2, 0, 1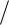2) . Форму матрицы упругих постоянных Cijkl Cmn взять из Таблицы 4, а значения упругих постоянных

-из задачи 2.

5.Определить упругость кристалла низкотемпературного кварца в

					C14 18.2 1010 ед.
направлении единичного вектора n(0, 1 2, 3 2) , если
СГСЕ. Форму матрицы упругих постоянных Cijkl Cmn					взять из Таблицы 4,

азначения упругих постоянных - из задачи 2.

6.Определить величину и характер деформаций, испытываемых кристаллом низкотемпературного кварца при его одноосном сжатии в направлении оси Х2 с усилием 103 Н / м2, если модули податливости кварца

имеют следующие значения (в ед. СГСЕ):

S	15.4 10 14 , S	22	128 10 14	, S	32	95.6 10 14	. Форму матрицы
12		22			32

упругих податливостей взять из Таблицы 4. Коэффициент перевода модулей податливости из системы СГСЕ в систему единиц СИ таков: 1 ед. СГСЕ = 1

см2/дин = 10 м2/Н.

7. Определить величину и характер деформаций, испытываемых кристаллом низкотемпературного кварца при его одноосном сжатии в

направлении оси Х3				с усилием 103 Н / м2, если его модули податливости
имеют			следующие			значения		(в	ед.	СГСЕ):
S	S	23	110. 10	14 , S	33	95.6 10	14 .	Форму	матрицы	упругих
13		23			33
постоянных			взять	из Таблицы 4.			Коэффициент		перевода	модулей

103

податливости из системы СГСЕ в систему единиц СИ таков: 1 ед. СГСЕ =1

см2/дин = 10 м2/Н.

8. Определить величину и характер деформаций, испытываемых кристаллом резорцина (точечная группа симметрии mm2, форма матрицы упругих постоянных приведена в Таблице 4) при его одноосном сжатии в

направлении	оси Х1	с усилием 103 Н / м2, если модули податливости
резорцина	имеют	следующие	значения	(в	ед.	СГСЕ):

S	19 10	12 , S	22	11 10	12 , S	33	15 10	12 , S	44	31 10	12 ,
11			22			33			44
S	23 10	12 , S	66	25 10	12 , S		4 10	12 , S		3 10	12 ,
55			66			12			13
S23	9 10	12 .

Коэффициент перевода модулей податливости из системы СГСЕ в систему единиц СИ таков: 1 ед. СГСЕ =1 см2/дин = 10 м2/Н.

9. Определить величину и характер деформаций, испытываемых кристаллом резорцина (точечная группа симметрии mm2, форма матрицы упругих постоянных приведена в Таблице 4) при его одноосном сжатии в

направлении	оси Х2	с усилием 103 Н / м2, если модули податливости
резорцина	имеют	следующие	значения	(в	ед.	СГСЕ):

S	19 10	12 , S	22	11 10	12 , S	33	15 10	12 , S	44	31 10	12 ,
11			22			33			44
S	23 10	12 , S	66	25 10	12 , S		4 10	12 , S		3 10	12 ,
55			66			12			13
S23	9 10	12 .

10. Определить величину и характер деформаций, испытываемых кристаллом резорцина (точечная группа симметрии mm2, форму матрицы упругих податливостей взять из Таблицы 4) при его одноосном сжатии в направлении оси Х3 с усилием 103 Н / м2, если модули податливости

104

резорцина имеют следующие значения (в ед. СГСЕ):

S	19 10	12 , S	22	11 10	12 , S	33	15 10	12 , S	44	31 10	12 ,
11			22			33			44
S	23 10	12 , S	66	25 10	12 , S		4 10	12 , S		3 10	12 ,
55			66			12			13
S23	9 10	12 .

11.Определить величину и характер упругих напряжений,

испытываемых кристаллом резорцина (точечная группа симметрии mm2,

форма матрицы упругих постоянных приведена в Таблице 4) при его

деформации на величину 10 6 вдоль оси Х1, если известно, что его упругие

постоянные		таковы	(в	ед.	СГСЕ):
C11	10 1010 , C22	14 1010 , C33	13 1010 , C44	3 1010 , C55	4 1010 ,
C66	4 1010 , C12	6 1010 , C13	7 1010 , C23 7 1010 .

Перевод из СГСЕ в систему СИ осуществляется с коэффициентом 1 ед. СГСЕ = 10-1 Н/м2.

12.Определить величину и характер упругих напряжений,

испытываемых кристаллом резорцина (точечная группа симметрии mm2,

форма матрицы упругих постоянных приведена в Таблице 4) при его

деформации на величину 10 6 вдоль оси Х2, если известно, что его упругие

постоянные принимают следующие численные				значения (в	ед. СГСЕ):
C11	10 1010 , C22	14 1010 , C33	13 1010 , C44	3 1010 , C55	4 1010 ,
C66	4 1010 , C12	6 1010 , C13	7 1010 , C23 7 1010 .

13.Определить величину и характер упругих напряжений,

испытываемых кристаллом резорцина (точечная группа симметрии mm2,

форма матрицы упругих постоянных приведена в Таблице 4) при его

деформации на величину 10 6 вдоль оси Х3, если известно, что его упругие

105

постоянные принимают следующие численные значения (в ед. СГСЕ):

C11	10 1010 , C22	14 1010 , C33	13 1010 , C44 3 1010 , C55 4 1010 ,
C66	4 1010 , C12	6 1010 , C13	7 1010 , C23 7 1010 .

14.Определить величину и характер упругих напряжений,

испытываемых кристаллом ниобата лития (точечная группа симметрии 3m,

форма матрицы упругих постоянных приведена в Таблице 4) при его

деформации на величину 10 6 вдоль оси Х1, если известно, что его упругие постоянные принимают следующие численные значения (в ед. СГСЕ):

C11	20 1010 , C22	C11, C33	24 1010 , C44	6 1010 , C55 C44 ,
C66	4 1010 , C12	5 1010 , C13	7.5 1010 , C23	0.9 1010.

15.Определить величину и характер упругих напряжений,

испытываемых кристаллом ниобата лития (точечная группа симметрии 3m,

форма матрицы упругих постоянных приведена в Таблице 4) при его

деформации на величину 10 6 вдоль оси Х2, если известно, что его упругие постоянные принимают следующие численные значения (в ед. СГСЕ):

C11	20 1010 , C22	C11, C33	24 1010 , C44	6 1010 , C55 C44 ,
C66	4 1010 , C12	5 1010 , C13	7.5 1010 , C23	0.9 1010.

16.Определить величину и характер упругих напряжений,

испытываемых кристаллом ниобата лития (точечная группа симметрии 3m,

форму матрицы упругих постоянных взять из Таблицы 4) при его

деформации на величину 10 6 вдоль оси Х3, если известно, что его упругие постоянные принимают следующие численные значения (в ед. СГСЕ):

C11	20 1010 , C22	C11, C33	24 1010 , C44	6 1010 , C55 C44 ,
C66	4 1010 , C12	5 1010 , C13	7.5 1010 , C23	0.9 1010.

106

17.Определить величину и характер упругих напряжений,

испытываемых кристаллом германия (точечная группа симметрии m3m,

форму матрицы упругих постоянных взять из Таблицы 4) при его

деформации на величину 10 6 вдоль оси Х3, если известно, что его упругие

постоянные принимают следующие численные значения	(в ед. СГСЕ):
C11 131 1010 , C22 C11, C33 C11, C44 68 1010 , C12	49 1010.

18.Определить величину и характер упругих напряжений,

испытываемых кристаллом хлористого калия (точечная группа симметрии m3m, форму матрицы упругих постоянных взять из Таблицы 4) при его

C11 39 1010 , C22 C11, C33 C11, C44 6.2 1010 , C12 6.2 1010.

19.Определить величину и характер упругих напряжений,

испытываемых кристаллом кремния (точечная группа симметрии m3m,

форму матрицы упругих постоянных взять из Таблицы 4) при его

C11 166 1010 , C22 C11, C33 C11, C44 80 1010 , C12 64 1010.

20.Определить величину и характер упругих напряжений,

испытываемых кристаллом арсенида галлия (точечная группа симметрии m3m, форму матрицы упругих постоянных взять из Таблицы 4) при его

C11 12. 1010 , C22 C11, C33 C11, C44 0.54 1010 , C12 0.59 1010.

107

ТАБЛИЦА 3

ФОРМА МАТРИЦ ПЬЕЗОМОДУЛЕЙ КРИСТАЛЛОВ РАЗЛИЧНЫХ СИНГОНИЙ

Т р и к л и н н а я с и н г о н и я

Класс 1

d11	d12	d13	d14	d15	d16
d 21	d 22	d 23	d 24	d 25	d 26
d31	d32	d33	d34	d35	d36

М о н о к л и н н а я с и н г о н и я

Класс 2, 2 || X 2 (обычн.ориентация)

0	0	0	d14	0	d16
d 21	d 2	d 23	0	d 25	0
0	0	0	d34	0	d36

		Класс m,
m	X 2 (обыч.ориентация)
d11	d12	d13	0	d15	0
0	0	0	d 24	0	d 26
d31	d32	d33	0	d35	0

	Класс 2, 2 \|\|			X 3
0	0	0	d14	d15	0
0	0	0	d 24	d 25	0
d31	d32	d33	0	0	d36
	Класс m, m			X 3
d11	d12	d13	0	0	d16
d 21	d 22	d 23	0	0	d 26
0	0	0	d34	d35	0

				Р о м б и ч е с к а я с и н г о н и я
			Класс 222					Класс mm2
0	0	0	d14	0	0	0	0	0	0	d15	0
0	0	0	0	d 25	0	0	0	0	d 24	0	0
0	0	0	0	0	d33	d31	d32	d33	0	0	0


			Т е т р а г о н а л ь н а я с и н г о н и я
		Класс 4
		Класс 4						Класс 4
0	0	0	d14	d15	0	0	0	0	d14	d15	0
0	0	0	d15	d14	0	0	0	0	d15	d14	0
d31	d31	d33	0	0	0	d31	d31	0	0	0	d36

108

			Класс 422					Класс 4mm
0	0	0	d14	0	0	0	0	0	0	d15	0
0	0	0	d15	d14	0	0	0	0	d15	0	0
0	0	0	0	0	0	d31	d31	d33	0	0	d36



Класс 4 2m,		2 \|\|	X .1 (обычная ориентация)
0	0	0	d14	0	0
0	0	0	0	d14	0
0	0	0	0	0	d36

			Т р и г о н а л ь н а я с и н г о н и я
		Класс 3									Класс 32
d11	d11	0	d14		d15	2d22		d11	d11	0	d14	0			0
d22	d22	0	d15		d14	2d11		0	0	0	0	d14			2d11
d31	d31	d33	0		0	0		0	0	0	0	0			0
Класс 3m, m		X1 (обыч.ориентац.)								Класс 3 m, m				X 2
0	0	0		0 d15		2d22		d11	d11		0	0 d15			0
d22	d22	0 d15			0	0		0	0		0 d15		0		2d11
d31	d31	d33		0	0	0		d31	d31	d33		0	0		0
			Г е к с а г о н а л ь н а я с и н г о н и я
		Класс 6								Класс 6mm
0	0	0 0		d14		d15	0	0	0		0	0 d15			0
0	0	0	0	d15		d14	0	0	0		0 d15			0 0
d31	d31	d33	0	0		0	0	d31	d31	d33		0		0 0

		Так же, как класс 4						Так же, как класс 4mm
				класс 622					класс 6
0	0	0	0	d14	0	0	d11	d11	0	0	0	2d 22
0	0	0	0	0	d14	0 0	d 22	d 22	0	0	0	2d11
0	0	0	0	0	0	0	0	0	0	0	0	0

109

					К у б и ч е с к а я с и н г о н и я
				Класс 432
				Класс 432				Класс 4 3m и класс 23
0	0	0	0	0	0	0	0	0	d14	0	0
0	0	0	0	0	0	0	0	0	0	d14	0
0	0	0	0	0	0	0	0	0	0	0	d14

Форма матриц пьезомодулей для некоторых пьезоэлектрических текстур

		Группа						Группа		m
0	0	0	d14	d15	0	0	0	0	0	d15	0
0	0	0	d15	d14	0	0	0	0	d15	0	0
d31	d31	d33	0	0	0	d31	d31	d33	0	0	0

			Группа		2
0	0	0	d14	0	0
0	0	0	0	d14	0
0	0	0	0	0	0

110

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1211 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.20235.18 Mб36Материалы для расчетов системы амортизации РЭС..pdf
#
05.02.2023297.76 Кб17Материалы и компоненты электронных средств..pdf
#
05.02.20232.71 Mб19Материалы и элементы электронной техники. Часть 1. Основы кристаллографии и кристаллофизики.pdf
#
05.02.20231.55 Mб9Материалы и элементы электронной техники. Часть 1.pdf
#
05.02.20231.91 Mб6Материалы и элементы электронной техники. Часть 2. Физические свойства кристаллов.pdf
#
05.02.20231.59 Mб11Материалы и элементы электронной техники. Часть 2.pdf
#
05.02.20231.1 Mб13Материалы и элементы электронной техники.-1.pdf
#
05.02.20231.54 Mб29Материалы и элементы электронной техники..pdf
#
05.02.2023172.91 Кб2Материалы нелинейной и интегральной оптики и динамической голографии.-1.pdf
#
05.02.2023178.76 Кб2Материалы нелинейной и интегральной оптики и динамической голографии..pdf
#
05.02.2023276.45 Кб3Материалы нелинейной оптики и динамической голографии.-1.pdf