
Материалы и элементы электронной техники. Часть 1
.pdf
где L - исходный линейный размер кристалла. Относительное изменение длины будет равно:
L/L = |
T . |
Величина физического свойства в заданном направлении определяется с |
|
помощью выражения |
|
( L/L)n = |
ij ni n j T . |
Распишем его в полном виде, что предполагает проведение суммирования по двум индексам
( L / L ) |
( |
11 |
n 2 |
12 |
n n |
13 |
n n |
21 |
n n |
2 |
22 |
n |
2 |
23 |
n n |
||||||
|
n |
|
|
1 |
|
1 |
2 |
1 |
3 |
1 |
|
2 |
2 |
3 |
|||||||
31 |
n n |
32 |
n n |
33 |
n |
2 ) |
T. |
|
|
|
|
|
|
|
|
|
|
||||
1 |
3 |
2 |
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Подставим в данное выражение сначала значения компонент единичного век-
тора n , у которого n3=0, тогда
( L / L ) |
( |
11 |
n 2 |
12 |
n n |
21 |
n n |
22 |
n 2 ) T. |
|||||||
|
|
n |
|
1 |
|
1 |
2 |
1 |
2 |
2 |
|
|||||
Теперь вместо |
ij |
в данное выражение подставим численные значения компо- |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нент тензора, а также численное значение изменения температуры |
|
|||||||||||||||
( L / L ) |
|
( 9.5 n |
2 |
|
4.8 n n |
2 |
4.8 n n |
2 |
9.5 n |
2 ) 10 4 |
T |
|||||
|
n |
|
|
1 |
|
1 |
|
|
1 |
|
2 |
|
|
|||
( 2 9.5 |
2 |
2 4.8 |
2 |
) 10 4 10 14.3 10 3 |
1.43 10 2 . |
|
||||||||||
4 |
4 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Задача 2. Определить величину электропроводности кристалла в направ-
лении, задаваемым единичным вектором n 0, 
 2
2 2,
2, 
 2
2 2 , если известно,
2 , если известно,
что тензор электропроводности данного кристалла в кристаллофизической сис-
теме координат имеет следующий вид:
51

15 4.5 0 4.5 15 0 10 7 , Ом -1 см -1. 0 0 88.8
Решение. Как и в предыдущей задаче, сначала запишем общее выраже-
ние для величины физического свойства в выбранном направлении
n  ij ni n j
ij ni n j  11
11  n12
n12  12n1n2
12n1n2  13n1n3
13n1n3  21n2n1
21n2n1  22n2 2
22n2 2  23n2n3
23n2n3 
 31n3n1
31n3n1  32n3n2
32n3n2  33n32 .
33n32 .
В данном выражении равны нулю все слагаемые, содержащие n1, а также и те,
которые содержат 13 , 31, 23 , 32 . Если эти слагаемые опустить, то полу-
чим, что требуемая величина равна
n |
n n |
j |
n 2 |
n 2 . |
ij i |
22 2 |
33 3 |
Подстановка в данное выражение численных значений компонент тензора и координат единичного вектора дает
n |
ij ni n j |
22n2 |
2 |
33n32 |
15 |
2 |
88.8 |
2 |
10 7 |
516. 10 7 Ом -1 см -1. |
|
4 |
4 |
||||||||
|
|
|
|
|
|
|
|
|
Задача 3. Вычислить величину абсолютной диэлектрической проницае-
|
|
|
|
|
|
|
|
|
|
мости |
а |
кристалла в направлении |
n |
2 2, 0, 2 2 , если тензор относи- |
|||||
|
|
|
|
|
|
|
|
|
|
тельной диэлектрической проницаемости |
о тн |
имеет вид |
|||||||
|
|
|
|
|
|
|
|
||
16 2.2 7.4
2.2 18 5.6 .
7.4 5.6 24
52

Решение. Величина абсолютной диэлектрической проницаемости а связана с относительной диэлектрической проницаемостью через диэлектриче-
скую проницаемость вакуума |
0 |
8.85 10 12 |
Ф / м |
|
|
|
|
|
|
|
|
а |
о тн |
0. |
Значит, требуемая величина определится с помощью следующего выражения
аn |
|
0 |
( |
|
n 2 |
|
n n |
n n |
n n |
n 2 |
n n |
||
|
|
11 1 |
12 1 2 |
13 1 3 |
21 2 1 |
22 2 |
23 2 3 |
||||||
n n |
|
32 |
n n |
33 |
n |
2 ). |
|
|
|
|
|||
31 |
3 |
1 |
|
3 |
2 |
|
3 |
|
|
|
|
||
Его упрощение возможно за счет использования симметричности тензора ди-
электрической проницаемости
аn |
0 |
( |
n 2 |
2 |
n n |
2 n n |
n 2 |
2 n n |
n 2 ). |
|
11 1 |
|
12 1 2 |
13 1 3 |
22 2 |
23 2 3 |
33 3 |
Теперь подставим в полученное выражение значения компонент единичного
вектора и учтем, что n2 = 0, тогда
|
|
( |
n 2 |
2 |
n n |
|
|
n |
2 ) 8.85 10 12 |
(16 |
2 |
2 7.4 |
2 |
24 |
2 |
) |
аn |
0 |
3 |
33 |
|
|
|
||||||||||
|
11 1 |
|
13 1 |
|
3 |
4 |
4 |
4 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
8.85 10 12 (8 7.4 12 ) |
8.85 10 12 27.4 2.4 10 10 (Ф / м ). |
|
|
|
||||||||||||
Итак, величина абсолютной диэлектрической проницаемости в направлении
вектора n составляет 2.4 10-10 Ф/м.
53

13.ВАРИАНТЫ ЗАДАНИЙ ПО ОПРЕДЕЛЕНИЮ ВЕЛИЧИНЫ ФИЗИЧЕСКОГО СВОЙСТВА
В ЗАДАННОМ НАПРАВЛЕНИИ
ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ № 2
1.Вычислить значение электропроводности кристалла симметрии m3m в на-
правлении единичного вектора n 1, 0, 0 , если тензор электропроводности
кристалла в кристаллофизической системе координат имеет вид:
88 0 0 0 88 0 10 6 , Ом -1 см -1 . 0 0 88
2. Вычислить значение электропроводности кристалла симметрии m3m в на-
правлении единичного вектора n 0, 1, 0 , если тензор электропроводности кристалла в кристаллофизической системе координат имеет вид:
, если тензор электропроводности кристалла в кристаллофизической системе координат имеет вид:
88 0 0 0 88 0 10 6 , Ом -1 см -1 . 0 0 88
3. Вычислить значение электропроводности кристалла симметрии mmm в на-
правлении единичного вектора n 0, 1, 0 , если тензор электропроводности кристалла в кристаллофизической системе координат имеет вид:
, если тензор электропроводности кристалла в кристаллофизической системе координат имеет вид:
77 0 0 0 88 0 10 6 , Ом -1 см -1 . 0 0 99
54

4. Вычислить значение электропроводности кристалла симметрии mmm в на-
правлении единичного вектора n 0, 0, 1 , если тензор электропроводности кристалла в кристаллофизической системе координат имеет вид:
, если тензор электропроводности кристалла в кристаллофизической системе координат имеет вид:
77 |
0 |
0 |
|
0 |
88 0 |
10 6 , Ом -1 см -1 . |
|
0 |
0 |
99 |
|
|
|
|
|
5. Вычислить значение электропроводности кристалла симметрии 6mm в на-
правлении единичного вектора n 
 2
2 2,
2, 
 2
2 2, 0 , если тензор электропро-
2, 0 , если тензор электропро-
водности кристалла в кристаллофизической системе координат имеет вид:
77 |
0 |
0 |
|
0 |
77 0 |
10 6 , Ом -1 см -1 . |
|
0 |
0 |
99 |
|
|
|
|
|
6. Вычислить значение электропроводности кристалла симметрии 6mm в на-
правлении единичного вектора n 0, 
 2
2 2,
2, 
 2
2 2
2 , если тензор электропро-
, если тензор электропро-
водности кристалла в кристаллофизической системе координат имеет вид:
77 0 0 0 77 0 10 6 , Ом -1 см -1 . 0 0 99
7. Вычислить значение электропроводности кристалла симметрии 6mm в на-
правлении единичного вектора n 
 3
3 3,
3, 
 3
3 3,
3, 
 3
3 3 , если тензор электро-
3 , если тензор электро-
проводности кристалла в кристаллофизической системе координат имеет вид:
55

77 |
0 |
0 |
|
0 |
77 0 |
10 6 , Ом -1 см -1 . |
|
0 |
0 |
99 |
|
|
|
|
|
8. Вычислить значение электропроводности кристалла симметрии 2 в направ-
лении единичного вектора n 
 3
3 3,
3, 
 3
3 3,
3, 
 3
3 3 , если тензор электропровод-
3 , если тензор электропровод-
ности кристалла в кристаллофизической системе координат имеет вид:
77 |
45 |
0 |
|
55 |
88 |
0 |
10 6 , Ом -1 см -1. |
0 |
0 |
99 |
|
|
|
|
|
9. Вычислить значение электропроводности кристалла симметрии 2 в направ-
лении единичного вектора n 
 2
2 2,
2, 
 2
2 2, 0
2, 0 , если тензор электропроводно-
, если тензор электропроводно-
сти кристалла в кристаллофизической системе координат имеет вид:
77 |
45 |
0 |
|
55 |
88 |
0 |
10 6 , Ом -1 см -1. |
0 |
0 |
99 |
|
|
|
|
|
10. Вычислить значение электропроводности кристалла симметрии 2 в направ-
лении единичного вектора n 
 2
2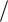 2, 0,
2, 0, 
 2
2 2
2 , если тензор электропроводно-
, если тензор электропроводно-
сти кристалла в кристаллофизической системе координат имеет вид:
77 |
45 |
0 |
|
55 |
88 |
0 |
10 6 , Ом -1 см -1. |
0 |
0 |
99 |
|
|
|
|
|
11. Вычислить значение электропроводности кристалла симметрии 2 в направ-
лении единичного вектора n 0, 
 2
2 2,
2, 
 2
2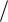 2
2 , если тензор электропроводно-
, если тензор электропроводно-
сти кристалла в кристаллофизической системе координат имеет вид:
56

77 |
45 |
0 |
|
55 |
88 |
0 |
10 6 , Ом -1 см -1. |
0 |
0 |
99 |
|
|
|
|
|
12. Вычислить значение электропроводности кристалла симметрии 4 в направ-
лении единичного вектора n 0, 
 2
2 2,
2, 
 2
2 2
2 , если тензор электропроводно-
, если тензор электропроводно-
сти кристалла в кристаллофизической системе координат имеет вид:
77 45 0 45 88 0 10 6 , Ом -1 см -1 .
00 99
13.Вычислить значение электропроводности кристалла симметрии 4 в направ-
лении единичного вектора n 
 3
3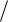 3,
3, 
 3
3 3,
3, 
 3
3 3 , если тензор электропровод-
3 , если тензор электропровод-
ности кристалла в кристаллофизической системе координат имеет вид:
77 45 0 45 88 0 10 6 , Ом -1 см -1 .
00 99
14.Вычислить значение электропроводности кристалла симметрии 4 в направ-
лении единичного вектора n 
 2
2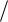 2, 0,
2, 0, 
 2
2 2
2 , если тензор электропроводно-
, если тензор электропроводно-
сти кристалла в кристаллофизической системе координат имеет вид:
77 45 0 45 88 0 10 6 , Ом -1 см -1 .
00 99
15.Вычислить значение абсолютной диэлектрической проницаемости кристал-
ла симметрии 4 в направлении единичного вектора n 
 3
3 3,
3, 
 3
3 3,
3, 
 3
3 3 , ес-
3 , ес-
57

ли тензор относительной диэлектрической проницаемости кристалла в кри-
сталлофизической системе координат имеет вид:
4.8 2.1 0
2.1 6.7 0 .
00 7.4
16.Вычислить значение абсолютной диэлектрической проницаемости кристал-
ла симметрии 4 в направлении единичного вектора n 
 2
2 2, 0,
2, 0, 
 2
2 2
2 , если
, если
тензор относительной диэлектрической проницаемости кристалла в кристал-
лофизической системе координат имеет вид:
4.8 2.1 0
2.1 6.7 0 .
00 7.4
17.Вычислить значение абсолютной диэлектрической проницаемости кристал-
ла симметрии 4 в направлении единичного вектора n 0, 
 2
2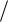 2,
2, 
 2
2 2
2 , если
, если
тензор относительной диэлектрической проницаемости кристалла в кристал-
лофизической системе координат имеет вид:
4.8 2.1 0
2.1 6.7 0 .
00 7.4
18.Вычислить значение абсолютной диэлектрической проницаемости кристал-
ла симметрии 2 в направлении единичного вектора n 0, 
 2
2 2,
2, 
 2
2 2
2 , если
, если
тензор относительной диэлектрической проницаемости кристалла в кристал-
лофизической системе координат имеет вид:
58

4.8 2.1 0
3.9 6.7 0 .
00 7.4
19.Вычислить значение абсолютной диэлектрической проницаемости кристал-
ла симметрии 2 в направлении единичного вектора n 
 2
2 2, 0,
2, 0, 
 2
2 2
2 , если
, если
тензор относительной диэлектрической проницаемости кристалла в кристал-
лофизической системе координат имеет вид:
4.8 2.1 0
3.9 6.7 0 .
00 7.4
20.Вычислить значение абсолютной диэлектрической проницаемости кристал-
ла симметрии 2 в направлении единичного вектора n 
 3
3 3,
3, 
 3
3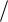 3,
3, 
 3
3 3 , ес-
3 , ес-
ли тензор относительной диэлектрической проницаемости кристалла в кри-
сталлофизической системе координат имеет вид:
4.8 2.1 0
3.9 6.7 0 .
0 0 7.4
59

14. ПРИМЕР РЕШЕНИЯ ЗАДАЧ
НА ОПРЕДЕЛЕНИЕ ВИДА ТЕНЗОРА
В НОВОЙ СИСТЕМЕ КООРДИНАТ
Задача 1. Определить вид и значения компонент тензора Т тетраго-
нального кристалла точечной симметрии 422 в новой системе координат, если в кристаллофизической системе координат он имеет вид:
4.8 0 0
0 4.8 0 ,
0 0 7.4
а матрица преобразования кристаллофизической системы координат в новую систему имеет следующий вид:
1 0 0
0 1 0 .
0 0 1
Решение. Для определения компонент тензора второго ранга при смене системы координат воспользуемся выражением
Тi' j' = Сi' k  Cj' l
Cj' l  Tkl ,
Tkl ,
где Сi' k и С j' l - компоненты матрицы преобразования системы координат, а
суммирование в правой части идет по индексам k и l, каждый из которых про-
бегает значения 1, 2, 3. Определим компоненту тензора Т11 в новой системе ко-
ординат сначала в общем виде, полагая в приведѐнном выше выражении
i'  j' 1' :
j' 1' :
T ' ' |
С ' |
C |
' |
T С ' |
2Т C ' |
C ' |
T C ' |
C ' |
T |
||||||
11 |
1 k 1 l |
kl |
|
|
|
11 |
11 |
11 12 |
12 |
11 13 |
13 |
||||
C ' |
C ' |
T С ' |
2Т |
22 |
C э |
C ' |
T C ' |
C ' T |
|
||||||
12 |
11 |
21 |
|
12 |
|
|
1 2 |
13 |
23 |
13 |
11 |
31 |
|
||
C ' |
C ' |
T |
|
С ' |
2 |
Т |
33 |
. |
|
|
|
|
|
|
|
13 |
12 |
32 |
|
13 |
|
|
|
|
|
|
|
|
|
||
60
