Исследование социально-экономических и политических процессов

32

никновении различий между моделью и реальной действительностью речь должна идти либо о корректировке модели, либо об изменении реальности, т.е. в соответствии с полученным на модели решением необходимо изменить свойства и структуру системы.

По природе используемых элементов модели подразделяются на содержательные (описательные), физические (аналоговые, электрические, графические, чертежи, фотографии) и ма-

тематические.

Под математической моделью понимается совокупность математических выражений, описывающих процесс и те условия (возмущения, ограничения), в которых он протекает. В свою очередь, в зависимости от используемого математического аппарата выделяют следующие виды математических моделей:

статические и динамические;

детерминированные и вероятностные;

аналитические и численные.

Статические модели описывают процесс в какой-либо момент времени, а динамические – отражают весь ход его развертывыания во времени. Детерминированные модели описывают процессы, в которых отсутствуют (не учитываются) случайные факторы, а вероятностные модели отражают случайные процессы – события. Аналитические модели описывают процесс в виде некоторых функциональных отношений или (и) логических условий. Численные модели отражают элементарные явления с сохранением их логической структуры и последовательности протекания во времени.

1.3.2 Математический аппарат описания

Многие социально-экономические и политические процессы, как правило, особенно на макро- и мезоуровнях, имеют достаточно длительную историю, в их отношении накоплен или может быть собран большой фактологический материал, позволяющий вскрыть закономерности и тенденции их развития. Сами же процессы обладают значительной инерционностью. В этом случае гипотеза о будущем развитии этих процессов в немалой степени может базироваться на анализе прошлого.

33

При построении математических моделей рассматриваемых процессов инертность следует понимать двояко:

как сохранение в основных чертах взаимосвязей прогнозируемых параметров с другими параметрами;

как сохранение общей тенденции изменения параметров (темпов, направления, колебаемости основных количественных показателей) во времени.

Наличие инерционности первого вида позволяет представлять процесс в виде аналитического выражения, которое связывает изменение результирующего показателя с изменением ряда

факторов, влияющих на него, т.е. поиску по выражению: y f (x1,x2,...,xn ).Зависимости такого типа получили название

уравнений регрессии либо моделей производственных функций. Инерционность второго вида позволяет подобрать аналитическую зависимость изменения наблюдаемого процесса во времени, т.е. определяется выражение типа yt f yt 1 . Эти зави-

симости относятся к классу трендовых моделей. Таким образом, описание протекания во времени социально-экономических и политических процессов осуществляется с помощью динамических временных рядов [18].

Предполагается, что с помощью таких рядов можно найти тенденцию (траекторию) процесса, выраженную в виде некоторой функции времени, называемой трендом. Количественное описание наблюдаемых тенденций лежит в основе статистических методов прогнозирования. Процесс описания состоит из трех основных этапов:

1)выбора типа кривой, форма которой соответствует характеру изменения динамического ряда;

2)определения численных значений параметров кривой;

3)экстраполяции процессов на базе выбранных уравнений трендов.

Вопрос о выборе формы кривой является основным при выравнивании ряда, при этом особое внимание должно уделяться характеристикам исходного ряда: параметрам изменения приростов, их преобразованиям.

Прежде чем перейти к краткому изложению этих вопросов, рассмотрим основные законы изменения известных в математи-

35

Многочлен первой степени применяется для описания процессов, равномерно развивающихся во времени. Парабола второй степени находит применение для равноускоренных процессов. И, наконец, для параболы третьей степени характерно изменение знака прироста один или два раза.

К числу наиболее часто используемых уравнений тренда для математического описания социально-экономических и политических процессов относятся следующие монотонно изме-

няющиеся кривые:

yt a b/t – гиперболическая кривая I типа;

yt 1/ a bt – гиперболическая кривая II типа;

yt t/ a bt – гиперболическая кривая III типа.

Простая экспоненциальная кривая характерна для процессов с постоянными темпами роста и прироста, причем для b 1 значения yi растут вместе с ростом t, и, наоборот, падают, ес-

ли b 1. Сведение экспоненты к линейному виду происходит следующим образом. Прологарифмировав выражение, получим

Более усложненным вариантом экспоненциальной кривой является логарифмическая парабола. Для логарифмической параболы темпы прироста линейно зависят от времени. Так, на-

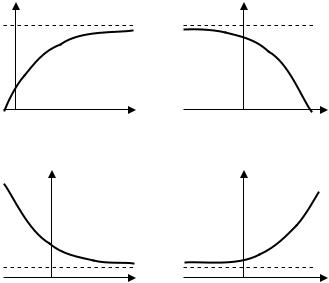
В случае, если процесс характеризуется насыщением, его описание имеет смысл лишь при помощи кривой, имеющей асимптоту, отличающуюся от нуля. Для описания этих тенденций наиболее простой зависимостью является модифицирован-

36

ная экспонента (рис. 1.12). Ее уравнение отличается от простой экспоненты только наличием дополнительного слагаемого k . При этом следует заметить, что для задания этого уравнения надо вычислять уже три параметра k , aи b . Чаще всего соци- ально-экономические процессы описываются кривой, приведенной на рис. 1.12а, где рост уровня происходит с замедлением, а сам он стремиться к некоторому пределу.

Рис. 1.12. Модифицированная экспонента

Степенная функция хорошо аппроксимирует показатели, непрерывно возрастающие во времени при положительном b и убывающие – при отрицательном. При b 1 это уравнение задает гиперболу, асимптотами которой служат оси координат. В экономике этому условию удовлетворяет кривая спроса с единичной эластичностью.

37

Гиперболические кривые первого, второго и третьего порядков описывают изменяющиеся процессы с насыщением и сводятся к линейным моделям путем простых и обратных преобразований зависимых и независимых переменных. Например, для функции y a b/t,t' 1/t, yt a bt' и для функции y 1/(a b)соответственно t' 1/ yt, yt a bt.

В экономических системах встречаются ситуации, когда динамика явления имеет следующие особенности: вначале наблюдается медленный темп изменения переменной, который в последующем убыстряется, достигает точки перегиба, после которой наблюдается замедление роста и, наконец, достижение фазы насыщения. Такими свойствами обладают логистические уравнения:

Обе кривые путем некоторых преобразований сводятся к уравнению модифицированной экспоненты. Например, прологарифмировав выражение кривой Гомперца, получим

ln yt lnk bt lna,

произведем замену переменных

ln yt yt , lnk , lna

и получим

yt a βbt.

Кривая Перла-Рида сводится к модифицированной экспоненте путем обратного преобразования y't 1/ yt и получения выражения

y't k abt.

В заключение следует отметить, что список кривых, применяемых для выравнивания динамических рядов, этим не ограничивается и может быть расширен. Вместе с тем предлагаемые кривые закрывают довольно большой спектр встречающихся тенденций в социальных, экономических, биологических и технических системах.

40

дифференцируема, то можно получить i f (x) 0 (i 1, n)

xi

– предельную эффективность, характеризующую отношение прироста выпуска продукции к малому приросту количества i- го ресурса. Вместе с тем, это предположение не всегда выполняется. Очевидно, что непрерывное увеличение такого фактора производства как земельные ресурсы, может привести к снижению качества их обработки, а отсюда и к уменьшению урожайности. Определение численных характеристик i позволяет ис-

следовать сложившиеся тенденции изменения эффективности использования соответствующего производственного фактора. В табл. 1.2 представлены возможные варианты ситуаций исследования эффективности.

Таблица 1.2 Варианты производственных ситуаций по эффективности

3) В условиях чисто экстенсивного роста производства увеличение затрат лишь одного производственного ресурса приводит к снижению эффективности его использования. Например, непрерывный рост основных фондов без увеличения обслужи-