
Элементарная математика для студентов (адаптационный курс)
..pdf
Пример 55(*). Решите уравнение lg2 x lg100x 4. |
|
||
Решение. Область |
допустимых значений уравнения x > 0. |
||
Перепишем уравнение в виде lg2 x (lg100 lgx) 4 |
или |
lg2 x 2 |
|
lgx 4 0. Обозначим |
y lgx и получим уравнение |
y2 |
y 6 0, |
корни которого по теореме Виета равны у = 3 и у = –2. Вернемся к исходной переменной. Для этого решим уравнения lgx 2
x 10 2 0,01 и lgx 3 x 103 1000. Оба корня принадлежат ОДЗ.
Ответ: 0,01; 1000.
Упражнения
Решите уравнения:
134. |
а) log4 x2 log4 x; |
б) lg(2x2 x 5) 2lg(x 1) 0. |
|
135. |
а) log3(x2 4x 3) log3(x 1); |
|
|
|
б) log2(x2 5x 3) log2(4x 5). |
|
|
136. |
а) lg(2x 5) lg(x 4) lg14; |
б) lgx lg(x 3) 1. |
|
137.а) log2(x 1) log2 x 2 log2 3;
б) log2(x 1) log2(2x 5) log2(3x 7).
138. |
а) logx 1(x2 3x 1) 1; |
б) logx(2x2 3x 4) 2. |
|||||||||
139. |
а) log2(x 14) log0,5(x 2) 6; |
б) 2log2(x2 9x 16) |
|
4 x. |
|||||||
140. |
а) log2(8x) log0,5 |
x |
8; |
б) log2(2x) |
|
3 |
3. |
||||
|
|
|
|
||||||||
|
2 |
|
|
|
log2 x |
||||||
141. |
а) lg(0,1x) log0,1(x 4) lg14; |
б) log3 x |
2 |
|
1; |
||||||
|
|
||||||||||
|
|
|
|
|
|
|
log3 x |
||||
142. |
а) log42 x 3log4 |
4 |
1; |
б) log0,52 x log0,5 2x 1. |
|||||||
|
|||||||||||
|
|
x |
|
|
|
|
|
|
|||
71
§ 15 Тригонометрические уравнения
Для решения тригонометрических уравнений необходимо знать обратные тригонометрические функции. Напомним эти понятия.
Арксинусом числа а называется угол такой, что sin a, при-
чем a [ 1;1] и arcsin( a) arcsina.
Арккосинусом числа а называется угол такой, что cos a,
причем a [ 1;1] и arccos( a) arccosa.
Арктангенсом числа а называется угол такой, что tg a
и arctg( a) arctga.
Все тригонометрические уравнения сводятся к одному из трех простейших уравнений:
а) sinx a x ( 1)k arcsina k, k Z |
при 1 a 1. При |
||||
|a| 1 уравнение sinx a действительных решений не имеет29; |
|||||
б) cosx a x arccosa 2 n, |
n Z при 1 a 1. При |a| 1 |
||||
уравнение cosx a действительных решений не имеет; |
|||||
в) tgx a, тогда x arctga k, |
k Z. |
|
|
|
|
Уравнение ctgx a |
при a 0 |
заменой |
ctgx |
1 |
сводится |
|
|||||
|
|
|
|
tgx |
|
к уравнению tgx a 1.
Более простой вид имеют формулы для решения простейших тригонометрических уравнений в частных случаях:
г) sinx 1, тогда x 2 n, n Z;
2
д) sinx 1, тогда x 2 n, n Z;
2
е) sinx 0, тогда x n, n Z; ж) cosx 1, тогда x 2 n, n Z;
з) cosx 1, тогда x 2 n, n Z;
и) cosx 0, тогда x n, n Z.
2
29 На множестве комплексных чисел уравнения sinx a и cosx a имеют решение для любого числа а.
72
Основные приемы решения тригонометрических уравнений — с помощью тождественных преобразований привести уравнение к одному из простейших. Например, перенести все слагаемые в левую часть уравнения и с помощью различных преобразований разложить ее на множители. К таким преобразованиям относятся группировка слагаемых, вынесение за скобки общего множителя, применение различных тригонометрических формул.
Второй класс тригонометрических уравнений – это уравнения, сводящиеся к одной тригонометрической функции. Тогда, выполнив замену переменной и решив алгебраическое уравнение, получим совокупность простейших тригонометрических уравнений.
Пример 56. Решите уравнение sin3x 0,5. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Решение. Это простейшее тригонометрическое |
|
|
уравнение. По |
|||||||||||||||||||
|
|
|
|
|
|
k |
|
1 |
|
k 1 |
|
|
|
|
|
|
|
k Z, или |
||||
формуле п. «а» 3x ( 1) |
|
arcsin |
|
|
k ( 1) |
|
|
k, |
|
|||||||||||||
|
|
|
6 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
x ( 1)k 1 |
|
|
|
k, k Z. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
18 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Ответ: ( 1)k 1 |
|
|
|
|
k, k Z. |
|||||||
|
|
|
|
|
|
|
|
|
|
18 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|||||
Пример 57. Найдите: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
а) общее решение уравнения cos2x 3cosx 1 0; |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
||||||
б) решения уравнения, принадлежащие отрезку |
|
|
|
; |
|
|
. |
|||||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
||||||
Решение. |
Распишем косинус двойного угла и получим уравне- |
|||||||||||||||||||||
ние 2cos2 x 1 3cosx 1 0. Обозначим t cosx |
и решим получен- |
ное после замены квадратное уравнение |
2t2 3t 2 0 |
t 3 
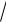 9 16 3 5. Его корни t = – 0,5 и t = 2. 4 4
9 16 3 5. Его корни t = – 0,5 и t = 2. 4 4
Уравнение cosx 2 на множестве действительных чисел решений не имеет30.
30 На множестве комплексных чисел это уравнение имеет решение. Так
как cosz 0,5(eiz e iz), то заменой |
t eiz оно сводится к квадратному |
73

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||
|
Уравнение cosx 0,5 |
|
имеет решение |
|
x arccos |
|
|
|
2 n |
|||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
n Z. |
|
|
|
||||||||||||||||
|
arccos |
|
|
|
2 n |
|
|
|
|
|
2 n |
|
|
|
|
|
2 n, |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Итак, общее решение уравнения x |
2 |
2 n, |
n Z. |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|||
|
Чтобы найти корни, принадлежащие отрезку |
|
|
|
|
|
|
, будем |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|||||
придавать n различные значения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
n = 0, тогда x |
2 |
|
5 |
; x |
2 |
|
|
|
5 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
. |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
3 |
|
2 2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
2 |
|
|
4 |
|
|
|
5 |
|
|
x |
2 |
||||||||||||||||||||||
|
n = –1, |
|
|
|
тогда |
|
|
|
2 |
|
|
|
|
|
|
; |
|
|
|
, |
|
|
|
|
2 |
|||||||||||||||||||||
|
|
|
|
3 |
|
3 |
|
|
|
|
|
|
|
3 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
8 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
; |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Итак, заданному отрезку принадлежат два решения: 2 ; 4 .
3 3
Ответ: а) 2 2 n, n Z; б) 2 ; 4 .
|
3 |
3 |
3 |
|
Упражнения |
|
|
Найдите общее решение уравнений. |
|
|
|
143. а) sin2x 1; |
б) sin4x 0,5; |
|
|
в) cos3x |
|
3 |
|
; |
|
|||
|
2 |
|
||||||
|
|
|
|
|
|
|||
|
|
|
|
|
||||
144. а) sin x |
|
|
1; |
|||||
|
||||||||
|
3 |
|
|
|
|
|||
|
|
|
|
1 |
|
|||
в) sin x |
|
|
|
|
|
|
; |
|
|
|
|
2 |
|||||
|
6 |
|
|
|
||||
145.а) sinx sin2x 0; в) cos2x 3sinx 1.
г) cos |
x |
|
1 |
. |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||||
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
2 |
|
|
|
|
|
||||||
б) cos x |
|
|
|
|
|
|
|
|
; |
|
|
|
||||
|
|
|
2 |
|
|
|
|
|||||||||
|
|
4 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
г) 4cosx cos |
|
|
x |
3. |
||||||||||||
|
||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
б) sin2x 3cosx 0;
уравнению t2 4t 1 0, которое имеет два различных корня, и решению показательных уравнений eiz t1,eiz t2.
74
146. |
а) cosx sin2x 0; |
б) 4cosx cos3 x 0; |
|
|
||||||
|
в) cos2x 1 cosx. |
б) sinx cos2 x 1. |
|
|
||||||
147. |
а) sin2x |
|
|
|
|
|||||
3sinx 0; |
|
|
||||||||
|
|
|
||||||||
148. |
а) 2cos2 x 7cosx 4 0; |
б) 3sin2 x 7cosx 3 0; |
||||||||
|
в) cos2x 5sinx 3 0; |
г) 2sin2 x 5cosx 4 0. |
||||||||
149. |
а) (sinx cosx)2 1,5; |
б) 0,5sin2x cos2 x 1; |
||||||||
|
в) sin4x cos4 x sin4 x; |
г) sin2x cosx cos3x. |
||||||||
150. |
а) |
|
sin2x 2sin2 x; |
б) sin2x |
|
3cosx |
|
2sinx. |
||
3 |
|
3 |
||||||||
§ 16 Системы и совокупности уравнений
Пусть даны два уравнения с двумя неизвестными f (x, у) = 0 и g (x, у) = 0. Поставим задачу, найти все пары чисел, удовлетворяющие этим уравнениям. В этом случае мы получаем систему двух уравне-
f (x,y) 0,
ний с двумя неизвестными
g(x,y) 0.
Решить систему уравнений — это значит найти все пары чисел (х0, у0), которые являются решением каждого из уравнений, или доказать, что таких пар чисел нет. Система, не имеющая решений, назы-
вается несовместной.
В общем случае система уравнений с n неизвестными — это множество уравнений с этими неизвестными31
f1(x1,x2,...,xn) 0,
|
|
(x1,x2,...,xn) 0, |
||||
f2 |
||||||
|
|
... ... ... |
|
|||
|
|
|
||||
f |
m |
(x ,x ,...,x |
n |
) 0. |
||
|
1 |
2 |
|
|
||
Решением системы уравнений называется упорядоченный набор |
||||||
чисел (значений неизвестных) |
(x(0),x(0) |
,...x(0)), при подстановке |
||||
|
|
|
1 |
|
2 |
n |
которых вместо неизвестных каждое из уравнений обращается в верное равенство.
31 Число уравнений не обязано совпадать с числом неизвестных.
75

Решать систему можно аналитически, выполняя равносильные преобразования входящих в систему уравнений. Например, выражая одно из неизвестных и подставляя его в другие уравнения системы, получим более простую систему32.
Наглядное представление о решении системы уравнений с двумя неизвестными дает ее графическое решение. Так как графиком каждого из уравнений является кривая, то решение системы уравнений — это множество точек пересечения заданных кривых.
Пусть дана система двух линейных уравнений с двумя неизвест-
ными a1x b1y c1, причем коэффициенты в правой части каждого
a2x b2y c2,
из уравнений не равны одновременно нулю. Рассмотрим основные методы решения такой системы.
1.Метод подстановки. Выражаем из первого уравнения одно из неизвестных и подставляем это выражение во второе уравнение. Решая полученное уравнение, находим одно неизвестное, а из формулы подстановки — второе неизвестное.
2.Метод сложения33. Умножим первое уравнение системы на
( a2), второе – на a1 (a1 0,a2 0) и сложим полученные уравнения
|
a1a2x a2b1y a2c1, |
a1x b1y c1, |
|
||||||||
|
a a |
x a b y a c |
или (a b |
|
a b )y a c |
a c . |
|||||
|
1 2 |
|
1 2 |
1 2 |
1 2 |
2 1 |
1 2 |
2 1 |
|||
Если ab a b 034, то |
y |
a1c2 |
a2c1 |
. |
Подставив найденное |
||||||
|
|
||||||||||
|
1 2 |
2 1 |
|
|
a1b2 |
a2b1 |
|
|
|||
|
|
|
|
|
|
|
|
||||
значение у в первое уравнение, получим x c1b2 c2b1 . a1b2 a2b1
32Существуют различные методы решения системы уравнений. Подход зависит от типа системы. Так, решение системы линейных уравнений полностью исследовано. Общего аналитического метода решения системы нелинейных уравнений не найдено.
33В курсе математики для уравнений и систем линейных уравнений с произвольным числом переменных этот метод называют методом исключения неизвестных или методом Гаусса.
34 В линейной алгебре выражение |
a1 |
b1 |
a b |
a b называют определи- |
||
|
a2 |
b2 |
1 |
2 |
2 |
1 |
|
|
|
|
|
||
телем 2-го порядка.
76
Итак, если a1b2 a2b1 0, то система имеет единственное реше-
ние x |
c1b2 c2b1 |
, y |
a1c2 a2c1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
a1b2 a2b1 |
|
a1b2 a2b1 |
|
a1 |
|
|
|
b1 |
|
|
|
c1 |
|
|
|||||||
Если ab a b |
0 |
, |
а |
a c |
a c 0 |
, т.е. |
|
|
|
|
|
|
|
, то система |
||||||||
|
|
|
|
|
||||||||||||||||||
1 2 |
2 1 |
|
|
|
|
1 2 |
2 1 |
|
a2 |
|
|
|
b2 |
|
|
|
c2 |
|
|
|||
решений не имеет. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
a1 |
|
|
|
b1 |
|
|
|
c1 |
|
|
||||
Если ab a b 0 |
, |
и |
a c |
a c 0 |
, т.е. |
|
|
|
|
|
, то система |
|||||||||||
|
|
|
|
|
|
|||||||||||||||||
1 2 |
2 1 |
|
|
|
|
1 2 |
2 1 |
|
a2 |
|
|
|
b2 |
|
|
|
c2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
имеет бесконечно много решений.
3.Графический метод. Каждому уравнению на плоскости соответствует прямая. Две прямые на плоскости могут либо пересекаться
водной точке (система имеет единственное решение), либо не иметь общих точек (система не имеет решений), либо совпадать (система имеет бесконечно много решений).
4.Метод определителей (метод Крамера). Этот метод в общем виде будет изучаться в разделе «Линейная алгебра».
Можно также рассматривать совокупность нескольких уравнений, например двух уравнений с двумя неизвестными
f (x,y) 0,g(x,y) 0.
Решить эту совокупность уравнений — это значит найти все пары чисел (х0, у0), каждая из которых является решением хотя бы одного из уравнений, а другое уравнение при этом имеет смысл.
Аналогично определяется совокупность уравнений с n неизвестными и ее решение. Множество уравнений
f1(x1,x2,...,xn) 0,f2(x1,x2,...,xn) 0,
... ... ...
fm(x1,x2,...,xn) 0
образует совокупность, если требуется найти все такие упорядоченные наборы чисел (x1(0),x2(0),...xn(0)), при каждом из которых хотя бы одно из уравнений совокупности обращается в верное числовое равенство, а другие уравнения имеют смысл.
77
Заметим, что уравнение f 2(x,y) g2(x,y) 0 равносильно сис-
f (x,y) 0,
теме уравнений а уравнение f (x,y) g(x,y) 0 равно-
g(x,y) 0,
f (x,y) 0,
сильно совокупности уравнений
g(x,y) 0.
3x
Пример 58. Решите систему уравнений
2x
2y 4,
5y 9.
Решение. Решим систему несколькими способами.
1. Метод подстановки. Из первого уравнения выразим у и подставим во второе уравнение
y 2 1,5x, |
y 2 1,5x, |
y 1, |
|
|
|
9,5x 19 |
|
2x 5(2 1,5x) 9 |
|
x 2. |
|
Итак, решение системы x = 2, y = –1.
2. Метод исключения неизвестных. Умножим первое уравнение
3x 2y 4 |
5 |
|
||
на 5, второе умножим на 2: |
|
2 |
2 |
|
2x 5y 9 |
||||
15x 10y 20, |
|
|
3х + 2у = 4 |
|
Из уравне- |
||||
2 |
||||
и сложим уравнения |
||||
4x 10y 18. |
|
|
|
|
ния 19х = 38 следует, что х = 2. Подставив значе- |
–1 |
|||
ние х в первое уравнение, найдем, что у = –1. |
2х – 5у = 9 |
|||
|
||||
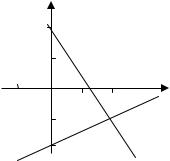
3. Графический метод. График |
каждого из |
|
||
уравнений системы — прямая на плоскости. Решение системы — это точка пересечения прямых.
Ответ: (2; –1)
Можно рассматривать также системы нелинейных уравнений. Если одно из уравнений системы является линейным, то можно применять метод подстановки.
78

2x y 4,
Пример 59. Решите систему уравнений
x2 5xy 3y2 4x 3.
Решение. Из первого уравнения выразим у и подставим во второе:
y 2x 4, |
y 2x 4, |
|||
|
2 5x(2x 4) 3(2x 4)2 4x 3, |
|
2 |
|
x |
3x |
24x 45 0, |
||
y 2x 4,
x2 8x 15 0.
Решив квадратное уравнение, найдем значения х: x1,2
4 
 16 15 x1 3, x2 5, а затем, подставив х в первое уравне-
16 15 x1 3, x2 5, а затем, подставив х в первое уравне-
ние, найдем у: у1 = 6 – 4 = 2, у2 = 10 – 4 = 6.
x |
3, |
и |
x |
2 |
5, |
||
Итак, |
1 |
2, |
|
y |
6. |
||
|
y |
|
|
2 |
|||
1 |
|
|
|
|
|||
Система имеет два решения.
Ответ: (3; 2), (5; 6).
7 x y xy 0,
Пример 60(*). Решите систему уравнений
5 y x xy 0.
(x y) xy 7,
Решение. Перепишем систему в виде
(x y) xy 5.
1-й |
способ. |
Сложим |
уравнения и |
(x y) xy 7, |
получим |
||||
|
у из |
|
|
x y 1. |
Выразим |
второго |
уравнения |
и подставим в первое: |
|
y x 1, |
Квадратное уравнение x2 x 6 0 имеет два корня |
|||
|
|
|||
1 x(x 1) 7. |
|
|
|
|
x1 = –2 и x2 = 3 (D = 25). Тогда у1 = –3 и у2 = 2. Система имеет два решения (–2; –3) и (3; 2).
2-й способ. |
Сделаем в системе замену |
переменных: пусть |
|
t x y, z xy. |
Система уравнений примет вид |
t z 7, |
Сложим |
|
|||
|
|
t z 5. |
|
уравнения системы и получим, что t = 1. Подставим найденное значения t в первое уравнение системы и получим, что z = 6. Следовательно, решение вспомогательной системы уравнений t = 1, z = 6.
79

|
Вернемся |
к |
исходным переменным |
и запишем систему: |
|||||
x y 1, |
|
|
|
|
|
|
|
|
|
|
Выразим из первого уравнения у и подставим во второе |
||||||||
|
xy 6. |
|
|
|
|
|
|
|
|
y x 1, |
|
|
|
|
|
|
|
|
|
|
Второе уравнение системы является квадратным и имеет |
||||||||
x(x 1) 6. |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
два решения |
x |
1 24 |
|
x 2, x |
2 |
3. |
Из первого уравнения |
||
|
|
|
|||||||
|
|
|
2 |
1 |
|
|
|||
|
|
|
|
|
|
|
|
||
для каждого значения х найдем соответствующее значение у. Решения
x |
2, |
и |
x |
2 |
3, |
системы 1 |
|
|
Система имеет два решения. |
||
y 1 3 |
|
y2 2. |
|||
Ответ: (–2; –3), (3; 2).
x2 5x 4 0,
Пример 61. Решите совокупность уравнений
x2 x 2 0.
Решение. Решением этой совокупности являются значения х, удовлетворяющие хотя бы одному уравнению. Каждое из уравнений является квадратным. Решим эти уравнения по теореме Виета. Корни первого уравнения x1 = –1, x2 = –4, корни второго уравнения x3 = –1, x4 = 2. Совокупность имеет три решения x1 = –4, x2 = –1, x3 = 2.
Ответ: –4; –1, 2.
Упражнения
Решите системы уравнений аналитически и графически.
x 3y 3; |
x 2y 6; |
151. a) |
б) |
3x 4y 17; |
5x 4y 44. |
2x 5y 1; |
4x y 10; |
152. a) |
б) |
3x 2y 11; |
3x 5y 19. |
Решите системы уравнений |
|
x 5y 8; |
y | x2 6x 5|; |
153. a) |
б) |
x2 4xy 21; |
y x 5. |
80
