Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Элементарная математика для студентов (адаптационный курс)

..pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

1.48 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 163 4 5 6 7 8 9 10 11 12 13 14 15 16 > Следующая >>>

x2 2x

7x 8

31.

а)

;

4 x

x2 4

x2 2x

x 2

б)

a2 4

(a 2)2

a 2

4 a2

2a a

3x 3

2x 3

x2 3x;

32.

а) x

x 2

x2 4x 4

(a 2)3

б)

2a.

33.

а)

8 x3

;

б)

27 x3

x3 64

2 2x 4 x2

2x 4

x2 3x 9 x

4x 16

34.

а)

25 x4/25

2/25

;

б)

x6/7 27

4/7

2/7

x2/25 5

x2/7 3

35.

а)

x2 12x 36

x2 22x 121

при –6 x 11;11

б)

x2 24x 144

10x

20x , если x [1; 10].

36.а) 8x x (x 8)2 32x , если x 15;

б) x4 10x2 25 x (x 6)2 4x 20, если х = 3.

37.	а)	3 1	1	: 3 2			2		;		б) 0,2						2,53							0,1 4		;
															0,25						0,027				16

		8				3
	в) 0,5							0,83						0,1 4						.
					0,64							0,064							81
		16 1/3				a 2 2/15										1/5						3/2
38.	а)												: 2a7					a4/3					;
									2
		a
									1		3/20 b3					1/4							4
	б) (9b6)1/5					:												: b 3/8					.
									3b	3					3

11 В задачах 35, 36 применить свойство модуля п. 8.

§ 2 Преобразование тригонометрических выражений

Пусть на плоскости задана декартова систе-
ма координат Oxy. Рассмотрим окружность ра-		М
ма координат Oxy. Рассмотрим окружность ра-	у	М
диуса R с центром в начале координат. Радиус	у


ОМ образует с положительным направлением
	О	х

оси ОХ угол . Если поворот вектора ОМ от по-


ложительного направления оси ОХ осуществля-
ется против часовой стрелки, то говорят, что

угол положительный, а если по часовой стрелке, то угол отрицательный. Углы в тригонометрии измеряются в градусах и радианах. Развернутый угол 180 равен радиан. Каждой точке на окружности соответствует бесконечно много углов, отличающихся на 360 или 2 радиан. Перевод из градусов в радианы и из радианов в градусы

180 (rad)

осуществляется с помощью пропорции	x(rad).

Определения основных тригонометрических функций12

Синусом угла называется отношение ординаты точки М

к радиусу окружности sin y . Синус определен для всех углов .

В 1-й и 2-й четвертях синус принимает положительные значения, в 3-й и 4-й — отрицательные.

Косинусом угла называется отношение абсциссы точки М

к радиусу окружности cos x . Косинус определен для всех

углов . В 1-й и 4-й четвертях косинус принимает положительные значения, во 2-й и 3-й — отрицательные.

12 В этом параграфе приведены определения и перечислены свойства тригонометрических выражений для действительных углов. Тригонометрические выражения для комплексного переменного определяются через показательные выражения, например sinz 0,5i eiz e iz , cosz 0,5 eiz e iz .

Тангенсом угла называется отношение ординаты точки М

к ее абсциссе tg y . Тангенс определен для всех углов , отличных x

от n (n Z).

Котангенсом угла называется отношение абсциссы точки М

к ее ординате ctg x . Котангенс определен для всех углов , y

отличных от n (n Z).

В 1-й и 3-й четвертях тангенс и котангенс принимают положительные значения, во 2-й и 4-й – отрицательные.

Тригонометрические функции острых углов (0 < < 90 ) имеют

следующий геометрический смысл: в произвольном		c
следующий геометрический смысл: в произвольном
прямоугольном треугольнике sin равен отношению
противолежащего катета к гипотенузе, cos — от- a
ношению прилежащего катета к гипотенузе, tg —
ношению прилежащего катета к гипотенузе, tg —		b
отношению противолежащего катета к прилежаще-		b
отношению противолежащего катета к прилежаще-

му, ctg — отношению прилежащего катета к противолежащему:

sin a , cos b, tg a . c c b

Если радиус окружности R = 1, то sin = y, cos = x.

Синус, тангенс и котангенс — нечетные функции, то есть sin(– ) = – sin , tg(– ) = – tg , ctg(– ) = – ctg , косинус — четная функция, то есть cos(– ) = cos . Если R (угол действительный), то синус и косинус функции ограниченные: |sin | 1, |cos | 113. Все четыре функции периодические: sin( 2 n) sin ,

cos( 2 n) cos	(период T = 2 ),	tg( n) tg ,	ctg( n)
ctg (период T =	) (n Z).

13 Синус и косинус комплексного аргумента могут принимать любое действительное или комплексное значение.

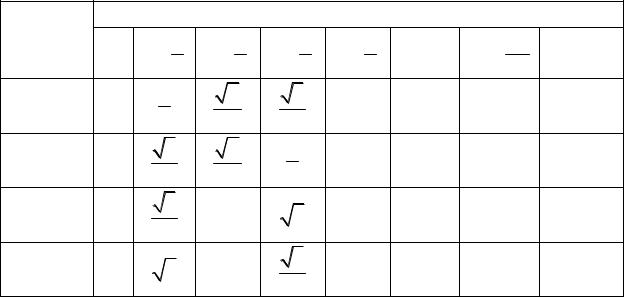
Значения тригонометрических функций в стандартных углах
					Углы, /rad
Функции	0/0	30/	45/	60/	90/	180/	270/3	360/2
		6	4	3	2		2
sin	0	1	2	3	1	0	–1	0
		2	2	2

cos	1	3	2	1	0	–1	0	–1
		2	2	2

tg	0	3	1	3	–	0	–	0
		3

ctg	–	3	1	3	0	–	0	–
				3

			Основные соотношения

между тригонометрическими функциями одного аргумента

sin2 cos2 1.

а) tg

sin

;

б) ctg

cos

;

в) tg ctg 1.

cos

sin

а) 1 tg2

;

б) 1 ctg2

cos2

sin2

Равенство п. 1 называется основным тригонометрическим то-

ждеством, а равенства п. 3 — следствиями из основного тождества.

Формулы сложения аргументов

4.sin( ) sin cos sin cos .

5.sin( ) sin cos sin cos .

6.cos( ) cos cos sin sin .

7.cos( ) cos cos sin sin .

Формулы приведения

Формулы приведения позволяют выразить значение тригонометрической функции любого угла через значение тригонометрической функции острого угла.

	90 –	90 +	180 –	180 +
sin	cos	cos	sin	–sin
cos	sin	–sin	–cos	–cos
tg	ctg	–ctg	–tg	tg
ctg	tg	–tg	–ctg	ctg

	270 –	270 +	360 –	360 +
sin	–cos	–cos	–sin	sin
cos	–sin	sin	cos	cos
tg	ctg	–ctg	–tg	tg
ctg	tg	–tg	–ctg	ctg

Анализируя формулы приведения, можно отметить следующее: если угол откладывается от горизонтального диаметра ( ,

2 ), то функция не меняется, если же угол откладывается от

			3
вертикального диаметра		,		, то функция меняется на
	2		2

кофункцию (синус косинус, тангенс котангенс). Знак в формуле совпадает со знаком исходной функции в той четверти, в которой лежит угол .

Тригонометрические функции двойных и половинных углов, формулы понижения степени

8.sin2 2sin cos .

9.cos2 cos2 sin2 2cos2 1 1 2sin2 .

	2sin2					1 cos
10.			1 cos ;	sin				.
		2			2	2


	2cos2						1 cos
11.			1 cos ;	cos					.
						2
		2			2

12. а) sin2

2tg

1 tg2

;

б) cos2

1 tg2

Формулы пп. 10

и 11,

записанные в

виде sin2

1 cos2

и cos2

называют формулами

понижения степени,

а формулы п. 12 применяют, выполняя универсальную тригономет-

рическую подстановку.

Формулы преобразования произведения функций в сумму

исуммы функций в произведение

13.sin cos 1 sin( ) sin( ) .

14.cos cos 1 cos( ) cos( ) . 2

15.sin sin 1 cos( ) cos( ) . 2

16.sin sin 2sin cos .

17.sin sin 2sin cos .

18.cos cos 2cos cos .

19.cos cos 2sin sin .

2	2
Пример 12. Вычислите 9sin , если cos					4		и 2 .
					4	2

				9
Решение. Из основного тригонометрического тождества получа-

ем sin 1 cos2 . Так как	2 , то sin 0. Таким обра-
						9		7	7.
	1	32	9	49
зом, 9sin 9 1 cos2 9		32		49
зом, 9sin 9 1 cos2 9				81
	81			81		9

Ответ: –7.

Пример 13. Вычислите 16sin , если tg											5			и		.
Пример 13. Вычислите 16sin , если tg														и	2	.
									39						2
Решение. По следствию к основному тригонометрическому
				1									1					, то
тождеству		sin2		1		.	Так	как	ctg				1				39
тождеству		sin2				.	Так	как	ctg			tg
			1 ctg2									tg			5
sin		1	(угол из второй четверти, синус положителен).


	1 ctg2
									16 5	10.
Итак, 16sin 16:				1	39		16	25	16 5
Итак, 16sin 16:				1			16	64	8
					25			64	8

Ответ: 10.

Пример 14. Вычислите 5sin150 3sin60 tg30 ctg45 .

Решение. Применим формулу приведения и вычислим значения тригонометрических функций в стандартных углах:

5sin150 3sin60 tg30 ctg45 5sin(180 30 )

3sin60 tg30 ctg45 5sin30 3sin60 tg30 ctg45

5 1 3 3 3 1 2,5 1,5 4. 2 2 3

Пример 15. В треугольнике АВС угол С – пря-

мой, АВ = 15, sin A		0,51. Найдите АС.
Решение. В треугольнике АВС выполняются
равенства sin A	BC	, cos A	AC	.
	AB
			AB

Ответ: 4.

СА

Из основного тригонометрического тождества выразим косинус

угла А: cosA 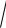1 sin2 A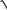 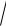1 0,51 0,7 (угол А — острый, поэтому косинус угла А положителен). Теперь нетрудно найти АС:

AC AB cosA 15 0,7 10,5.

Ответ: 10,5.

Пример 16(*). Вычислите значение тригонометрического выра-

жения cos340 sin20 cos20 sin20 ctg220 . sin155 sin65 cos65 cos25

Решение. Применим формулы приведения:

cos340 sin20 cos20 sin20 ctg220 sin155 sin65 cos65 cos25

cos(360 20 )sin20 cos20 sin20 sin(180 25 )sin65 cos65 cos25

ctg(180 40 ) cos20 sin20 cos20 sin20 ctg40 . sin25 sin65 cos65 cos25

Применим формулы синуса двойного угла и косинуса разности двух углов:

	2cos20 sin20			ctg40	sin40 ctg40
cos65 cos25 sin25 sin65
					cos(65 25 )
	sin40	cos40	1.
	cos40	sin40

Ответ: 1.

Пример 17(*). Вычислите sin2 sin2 3 sin2 5 sin2 7 .

					8				8	8		8
Решение. Применим формулы понижения степени
	1			1					3 1		3	1
sin2	1			1		2		2	3 1		3	1		2	,
		1 cos					, sin			1 cos
		1 cos		2	2		, sin			1 cos	4	2	2
	8 2		4	2	2				8 2		4	2	2

	2	5 1		5	1	2		2	7	1		7	1
sin			1 cos				, sin				1 cos
				4	2	2			8	2		4	2
		8 2

Значения косинусов нашли через формулы приведения:

	3									2
cos		cos				cos					,
cos	4	cos		4		cos	4		2		,
	4			4			4		2
	5
	5									2
cos		cos				cos						,
cos	4	cos		4		cos	4		2			,
	4			4			4		2
	7
	7								2	.
cos		cos	2			cos
cos	4	cos	2		4	cos	4
	4				4		4	2

Итак, sin2 sin2 3 sin2 5 sin2 7

				8				8		8			8
	1				1				1			1			2.
			2				2				2			2
		2				2				2		2
2				2				2					2

2 . 2

cos 2cos2 1

Ответ: 2.

Пример 18(*). Вычислите 3cos2 4sin2 7, если tg 0,5.

Решение.

2tg

1 tg2

(формулы 12),

sin2

, cos2

1 tg2

поэтому sin2

2 0,5

0,8;

cos2

0,25

0,6

и 3cos2

1 0,25

0,25

4sin2 7 3 0,6 4 0,8 7 12.

Ответ: 12.

Пример 19(*). Упростите выражение 1 cos cos2 cos3 .

Решение. Для упрощения выражения применим формулы двойного и половинного углов и формулу преобразования суммы косинусов в произведение

1 cos cos2 cos3		(1 cos2 ) (cos cos3 )
cos 2cos2 1
		cos (2cos2 1)

2cos2 2 cos3 2 cos3 2 2cos2 2cos cos2

cos cos2

2cos (cos cos2 )

		2cos .

cos cos2

Ответ: 2cos .

Упражнения

Вычислите

39.	8sin , если cos		7		и 0					.
			4

					1		2
40.							и	.
		10cos , если sin
		10cos , если sin
					10		2
41. 17cos , если sin				15		и					3	.
41. 17cos , если sin						и						.
			17				2
42.	5tg , если sin		4		и 0				.
42.	5tg , если sin				и 0				.
			41				2