
Спецглавы математики. Часть 1
.pdfМинистерство образования Российской Федерации
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
З.А. Смыслова
СПЕЦГЛАВЫ МАТЕМАТИКИ
Часть 1
Учебное пособие
2000
Смыслова З.А.
Спецглавы математики. Часть 1: Учебное пособие. − Томск: Томский межвузовский центр дистанционного образования, 2000. – 96 с.
Данное учебное пособие содержит теоретический материал по теории множеств и комбинаторике, математической логике, основам теории групп, а также варианты двух контрольных работ для студентов специальности 2202 «Автоматизированные системы обработки информации и управления», обучающихся по дистанционной форме. Приведены примеры решения задач контрольных работ.
Пособие может быть использовано для студентов заочной и дневной форм обучения.
Смыслова Зинаида Александровна, 2000
Томский межвузовский центр
дистанционного образования, |
2000 |
3
СОДЕРЖАНИЕ
1. Теория множеств . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
5 |
1.1. Множества и операции над ними . . . . . . . . . . . . . . . . . . . . . . . |
5 |
1.1.1. Понятие множества . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
5 |
1.1.2. Способы задания множеств . . . . . . . . . . . . . . . . . . . . . . |
5 |
1.1.3. Основные определения . . . . . . . . . . . . . . . . . . . . . . . . . . |
6 |
1.1.4. Диаграмма Эйлера – Венна . . . . . . . . . . . . . . . . . . . . . . . |
6 |
1.1.5. Операции над множествами . . . . . . . . . . . . . . . . . . . . . . |
7 |
1.1.6. Системы множеств . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
8 |
1.1.7. Законы алгебры множеств . . . . . . . . . . . . . . . . . . . . . . . |
10 |
1.1.8. Решение задач 1,2,3 контрольной работы № 1 . . . . . . . |
11 |
1.1.9. Контрольные вопросы и упражнения . . . . . . . . . . . . . . |
14 |
1.2. Бинарные отношения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
15 |
1.2.1. Декартово произведение множеств. Соответствие |
|
множеств . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
15 |
1.2.2. Определение бинарного отношения . . . . . . . . . . . . . . . |
17 |
1.2.3. Способы задания бинарного отношения . . . . . . . . . . . . |
17 |
1.2.4. Свойства бинарных отношений . . . . . . . . . . . . . . . . . . . |
19 |
1.2.5. Отношения эквивалентности . . . . . . . . . . . . . . . . . . . . . |
20 |
1.2.6. Отношения порядка . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
23 |
1.2.7. Частично упорядоченные множества . . . . . . . . . . . . . . |
24 |
1.2.8. Диаграммы Хассе . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
24 |
1.2.9. Изоморфизм частично упорядоченных множеств . . . . |
25 |
1.2.10. Решение задач 5, 6 контрольной работы № 1 . . . . . . . |
28 |
1.2.11. Контрольные вопросы и упражнения . . . . . . . . . . . . . |
31 |
1.3. Реляционная алгебра . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
32 |
1.3.1. Применение отношений при обработке данных . . . . . . |
32 |
1.3.2. Теоретико-множественные операции реляционной |
|
алгебры . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
32 |
1.3.3. Специальные операции реляционной алгебры . . . . . . . |
34 |
1.3.4. Решение задачи 7 контрольной работы № 1 . . . . . . . . . |
36 |
1.3.5. Контрольные вопросы и упражнения . . . . . . . . . . . . . . |
37 |
1.4. Конечные и бесконечные множества . . . . . . . . . . . . . . . . . . . |
37 |
1.4.1. Равномощные множества . . . . . . . . . . . . . . . . . . . . . . . . |
37 |
1.4.2. Классы равномощных множеств . . . . . . . . . . . . . . . . . . |
39 |
1.4.3. Сравнение множеств по мощности . . . . . . . . . . . . . . . . |
39 |
1.4.4. Свойства конечных множеств . . . . . . . . . . . . . . . . . . . . |
41 |
1.4.5. Определение счетного множества . . . . . . . . . . . . . . . . . |
44 |
1.4.6. Свойства счетных множеств . . . . . . . . . . . . . . . . . . . . . . |
45 |
1.4.7. Несчетные множества . . . . . . . . . . . . . . . . . . . . . . . . . . . |
47 |
4 |
|
1.4.8. Булеан конечного множества. Выводы. . . . . . . . . . . . . . |
48 |
1.4.9. Решение задач 8,9 контрольной работы № 1 . . . . . . . . |
50 |
1.4.10. Контрольные вопросы и упражнения . . . . . . . . . . . . . |
51 |
2. Комбинаторика. Основы теории групп . . . . . . . . . . . . . . . . . . . . . . |
52 |
2.1. Комбинаторика . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
52 |
2.1.1. Задачи комбинаторики . . . . . . . . . . . . . . . . . . . . . . . . . . |
52 |
2.1.2. Типы выборок . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
52 |
2.1.3. Основные правила комбинаторики . . . . . . . . . . . . . . . . |
54 |
2.1.4. Размещения с повторениями . . . . . . . . . . . . . . . . . . . . . . |
54 |
2.1.5. Размещения без повторений . . . . . . . . . . . . . . . . . . . . . . |
55 |
2.1.6. Перестановки без повторений . . . . . . . . . . . . . . . . . . . . |
56 |
2.1.7. Перестановки с повторениями . . . . . . . . . . . . . . . . . . . . |
56 |
2.1.8. Сочетания . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
57 |
2.1.9. Сочетания с повторениями . . . . . . . . . . . . . . . . . . . . . . . |
58 |
2.1.10. Решение задач 2, 3 контрольной работы № 2 . . . . . . . |
59 |
2.1.11. Бином Ньютона . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
59 |
2.1.12. Свойства биномиальных коэффициентов . . . . . . . . . . |
61 |
2.1.13. Приближенные вычисления с помощью бинома |
|
Ньютона . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
63 |
2.1.14. Контрольные вопросы и упражнения . . . . . . . . . . . . . |
64 |
2.2. Группы подстановок . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
66 |
2.2.1. Понятие группы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
66 |
2.2.2. Группа подстановок . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
67 |
2.2.3. Изоморфизм групп . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
70 |
2.2.4. Самосовмещения фигур . . . . . . . . . . . . . . . . . . . . . . . . . |
72 |
2.2.5. Контрольные вопросы и упражнения . . . . . . . . . . . . . . |
73 |
Приложение 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
74 |
Приложение 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
87 |

5
1.ТЕОРИЯ МНОЖЕСТВ
1.1.Множества и операции над ними
1.1.1.Понятие множества
Теория множеств опирается на три первичных понятия:
1)множество;
2)элемент;
3)принадлежность.
Строгого определения этим понятиям не дается, описывается только их применение. Для этих понятий используются обозначения: “ a A ”- элемент а принадлежит множеству А; “ c A ” - элемент с не принадлежит множеству А.
Говоря о некотором множестве, мы требуем его:
1)целостности, т.е. возможности рассматривать его как отдельный объект;
2)различимости его элементов;
3)неупорядоченности элементов.
Поэтому записи {a,b} и {b, a} определяют одно и то же множест-
во.
1.1.2. Способы задания множеств
Множество можно задать, перечислив |
все его |
элементы: |
A ={a,b, c} , B ={−1,3,6,8} . Порядок записи |
элементов |
множества |
произволен. Часто задают множество, указав его характеристическое свойство, которое для каждого элемента позволяет выяснить, принадлежит он множеству или нет.
Например,
B ={ x x – целый корень уравнения 2x3 − x2 +1 = 0} ,
C ={x −1 ≤ x ≤ 7, x – целое}.
В дальнейшем для известных числовых множеств будут использоваться обозначения:
Ν = { 1,2,3,…} – множество натуральных чисел;
Z = { …, -2,-1,0,1,2,…} – множество целых чисел;
Q– множество рациональных чисел;
R– множество действительных чисел.
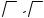
6
1.1.3. Основные определения
Пустым множеством называется множество , не содержащее ни одного элемента, т.е. для любого элемента x выполняется x .
Универсальным называется множество U всех элементов, рассматриваемых в данной задаче.
Пример.
Пусть U = Z и требуется найти все решения уравнения x2 = 2 .
Множество М решений этой задачи есть пустое множество: М = . Пусть теперь U = R. Тогда множество М решений уравнения
x2 = 2 не пусто: М = {− 2 ,
2 ,  2} .
2} .
Будем говорить, что множество А включается во множество В (A B) , если каждый элемент множества А является элементом мно-
жества В ( говорят также, что А является подмножеством множества В). Из определения включения следуют свойства:
1)A A для любого множества А;
2)Если A B и B C , то A C ;
3)A для любого множества А;
4)A U для любого множества А.
Подмножество A B называется собственным подмножеством
множества В ( A B - строгое включение), если А не пусто и не совпадает с В. Например, имеют место строгие включения: N Z Q R.
Определим понятие равенства множеств: А=В тогда и только тогда, когда одновременно выполняются два включения A B и
B A , т.е. каждый элемент множества А является элементом множе-
ства В и каждый элемент множества В является элементом множества
А:
x A x B, A = B
x B x A.
Свойства равенства множеств:
1)для любого А справедливо А=A;
2)если А=В, то и В=A;
3)если А=В и В=C, то A=C.
1.1.4. Диаграммы Эйлера – Венна
Эти диаграммы применяются для наглядного изображения множеств и их взаимного расположения.

7
U
A B
Рис. 1.1 Диаграмма Эйлера-Венна
Универсальное множество U изображается в виде прямоугольника, а произвольные множества – подмножества универсального – в виде кругов (рис. 1.1).
При этом возможны следующие случаи взаимного расположения двух множеств А и В:
1) одно из множеств строго включается в другое ( A B или
B A );
2)множества равны;
3)множества не имеют общих элементов;
4)множества находятся в общем положении, т.е. не подходит ни один из вышеперечисленных случаев, и множества расположены как на рис. 1.1.
1.1.5. Операции над множествами
Объединением множеств А и В называется множество A B , состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из множеств А или В (рис. 1.2, а).
Пример.
Если A ={0,1,2}, B ={−1,2,3} , то A B ={−1,0,1,2,3} .
|
|
U |
U |
A |
B |
A |
B |
а) |
б) |
Рис. 1.2. Операции над множествами: а) объединение множеств; б) пересечение множеств
8
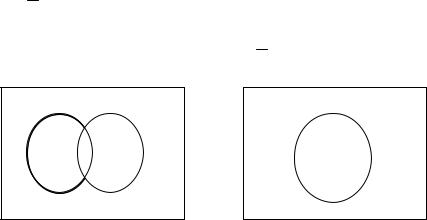
Пересечением множеств А и В называется множество A ∩ B , состоящее из тех и только тех элементов, которые принадлежат одновременно и множеству А, и множеству В (рис. 1.2, б).
Пример.
Если A ={0,1,2}, B ={−1,2,3} , то A ∩ B ={2} .
Разностью множеств А и В называется множество A \ B тех и только тех элементов, которые принадлежат множеству А и не принадлежат множеству В (рис. 1.3, а).
Пример.
A \ B ={0,1,2} \ {−1,2,3} ={0,1} ;
B \ A ={−1,2,3} \ {0,1,2} ={−1,3} .
Дополнением множества А до универсального U называется множество A =U \ A (рис. 1.3, б).
Пример.
Если A ={0,1,2} , U ={0,1,2,3,4,5}, то A =U \ A ={3,4,5}.
|
U |
U |
A |
B |
A |
а) |
б) |
Рис. 1.3. Операции над множествами: а) разность множеств A и B;
б) дополнение множества A
1.1.6. Системы множеств
Элементы множества |
сами могут быть множествами: |
A ={{1},{2,3},{1,2}}; в таком |
случае удобно говорить о системе мно- |
жеств. Рассмотрим такие системы множеств, как булеан, разбиение и покрытие множеств.
Булеаном B(Х) множества Х называется множество всех подмножеств множества Х. Например, для множества X ={0,1} булеаном яв-
ляется множество B ( X ) = { ,{0},{1},{0,1} }.

9
Разбиением R(Х) множества Х называется система его непустых непересекающихся подмножеств, в объединении дающая множество Х
(рис. 1.4).
U
X X1 X2
X3 X4
Рис. 1.4. Разбиение множества R (X ) ={X1, X 2 , X3, X 4}
Например, для множества X ={1,2,3,4,5} можно построить разбиение R1 (X ) = {{1,2},{3,4,5}}, состоящее из двух элементов (они называются блоками разбиения), или разбиение R2 (X ) ={{1},{2,5},{3},{4}}
– из четырех блоков; возможны и другие разбиения этого множества Х. Покрытием P(X) множества X называется система его непустых
подмножеств, в объединении дающая множество X (рис. 1.5).
U
X1 X2
X3
Рис. 1.5. Покрытие множества
P(X)={X1, X2, X3}
В этом определении отсутствует слово “непересекающаяся” – т.е. блоки могут иметь общие элементы.
Пример.
Для множества X ={1, 2,3, 4,5} покрытиями являются системы множеств P1(X ) = {{1},{1, 2,3},{3, 4,5}} и P2 (X ) = {{1, 2},{2,3, 4},{5}}.
10
1.1.7. Законы алгебры множеств
Так же, как операции обычной алгебры, операции над множествами выполняются по законам (табл. 1.1), которые доказываются на основе введенных выше определений. Особенностью алгебры множеств является закон идемпотентности, благодаря которому в алгебре множеств нет числовых коэффициентов и степеней.
|
|
|
|
|
|
|
|
|
|
|
|
Законы алгебры множеств |
Таблица 1.1 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
№ |
|
|
|
|
|
|
|
|
|
|
Формулы |
Название |
|||||||||||||||
1 |
|
|
A∩ = ; A = A; A∩ |
|
|
= |
Свойства пустого мно- |
||||||||||||||||||||
|
A |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
жества |
|
2 |
|
|
A U = U; A∩U = A; A Ā = U |
Свойства универсаль- |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ного множества |
|
3 |
|
|
|
∩ |
|
∩ |
A; A |
|
|
|
|
Закон |
коммутативно- |
||||||||||||||
|
|
|
A B = B |
|
|
|
B = B A |
сти |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
∩ |
|
∩ |
|
∩ |
|
|
∩ |
Закон ассоциативности |
||||||||||||||
|
|
|
(А В) С=А (В С); |
|
|
||||||||||||||||||||||
|
|
|
(А В) С=А (В С) |
|
|
||||||||||||||||||||||
5 |
|
|
А∩(В С)= (А∩В) (А∩С); |
Закон |
дистрибутивно- |
||||||||||||||||||||||
|
|
|
А (В∩С)= (А В)∩(А С) |
сти |
|
||||||||||||||||||||||
6 |
|
|
|
|
|
=А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Закон двойного допол- |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нения |
|
7 |
|
|
А∩А=А; А А=А |
|
|
|
|
|
|
|
|
|
Законы |
идемпотентно- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сти |
|
8 |
|
|
|
|
|
|
|
= |
|
∩ |
|
; |
|
= |
|
|
|
; |
Законы де Моргана |
||||||||
|
|
А В |
А ∩ В |
||||||||||||||||||||||||
|
|
А |
В |
А |
В |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
9 |
|
|
|
|
∩ |
|
|
|
|
∩ |
|
|
Законы поглощения |
||||||||||||||
|
|
|
А (А В)=А; А |
|
|
|
(А В)=А |
|
|
||||||||||||||||||
|
Докажем закон дистрибутивности |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
А (В∩С)= (А В)∩(А С). |
(1.1) |
|||||||||||||||
Обозначим X левую часть равенства (1.1), Y – правую. Согласно определению равенства множеств покажем, что выполняются одновременно X Y и Y X .
Пусть x – произвольная точка из множества X=А (В∩С). Тогда
по определению объединения множеств ( x A |
или x (B ∩C) ). Да- |
лее по определению пересечения множеств |
( x A или(x B и |
x C) ). Следовательно, |
|
((x A или x B) и ( x A или x C)) ((x A B) и (x A C))
x (A B) ∩(A C) =Y .
