Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Теория автоматического управления

..pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

1.36 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 177 8 9 10 11 12 13 14 15 16 17 > Следующая >>>

В схеме на рис. 3.6, е τ <T , и для такого звена k = R3 ,

τ = (R1 + R2 )C , T = R2C .

3.2.1.7 Изодромное звено

Это звено представляет последовательное соединение интегрирующего и форсирующего звеньев, его передаточная функция имеет вид

W ( p) =Wинт( p) Wфорс( p) = k (τp +1) .

Какивпредыдущемслучае, ЛАЧХиЛФЧХскладываются, т.е.

G(ω) = G	(ω) +G		(ω) = 20lg k + 20lg				ω2τ2 +1 −20lg ω,
инт	форс
ϕ(ω) = ϕ		(ω) + ϕ		(ω) = arctg			(ω τ) − π .
	инт		форс				2
							2
На рис. 3.7, а, приведены ЛАЧХ и ЛФЧХ изодромного зве-
на. До частоты сопряжения ω =					1	ЛАЧХ проходит с наклоном
на. До частоты сопряжения ω =						ЛАЧХ проходит с наклоном
			c		τ

–20 дБ/дек, а после нее — горизонтально. Суммарная ЛФЧХ представляет собой ЛФЧХ форсирующего звена, смещенную за

счет интегрирующего звена на угол − π .

Переходная функция изодромного звена может быть выведена по формуле (2.16), поскольку изображение выходной величины будет содержать нулевой полюс кратности 2, т.е.


h(t) =	d	B( p)e pt	\|		=	d	k (τp +1)e pt	\|	= k (τ+t ) .
h(t) =		B( p)e pt	\|	p=0	=		k (τp +1)e pt	\|	= k (τ+t ) .
	dp			p=0		dp			p=0

Переходная характеристика звена (рис. 3.7, б) будет представлять собой линейную зависимость, смещенную относительно начала координат на величину kτ.

		61
G(ω)	–20дБ/дек	h(t)
G0
	1	kτ
0	1	lg ω
0	lg τ
	lg τ
ϕ(ω)
π		0	t
2		0	t
2		б
π
4		C	R2
		C	R2
0		lg ω
− π		R1
− π
4
− π
2	а	в
	а	в

Рис. 3.7 — ЛАЧХ и ЛФЧХ (а), переходная характеристика (б) изодромного звена и его реализация на операционном усилителе (в)

На рис. 3.7, в приведена реализация изодромного звена на операционном усилителе. Для такой схемы

Zвх( p) = R1, Zос( p) = R2 + 1 = R2Cp +1 .

Cp Cp

Передаточная функция

R2Cp +1

k (τp +1)

W ( p) = −

= −

R1C

где k =

, τ = R C .

R1C

3.2.1.8 Реальное дифференцирующее звено

Такое звено является последовательным соединением дифференцирующего и инерционного звеньев, его передаточная функция имеет вид

W ( p) =W			( p)	W	( p) =	kp	.

		дифф		ин		Tp +1

ЛАЧХ и ЛФЧХ складываются, т.е.
G(ω) = Gдифф(ω) +Gин(ω) = 20lg k + 20lg ω− 20lg ω2T 2 +1 ,
ϕ(ω) = ϕ	дифф	(ω) + ϕ		(ω) = π −arctg (ω T ) .
			ин		2

На рис. 3.8, а приведены логарифмические частотные ха-

рактеристики реального дифференцирующего звена. До частоты

сопряжения ω =	1	ЛАЧХ проходит с наклоном +20 дБ/дек, а

c	T

после нее — горизонтально. Суммарная ЛФЧХ представляет собой ЛФЧХ инерционного звена, смещенную за счет диффе-

ренцирующего звена на угол π .

Расчетное выражение для переходной функции этого звена

может быть получено

по

формуле

(2.14)

при B( p) = kp ,

A( p) = Tp +1 , A′( p) =T , p =

−

p t

e T

h(t) =

B(0)

B( p1)e

= 0

−

A(0)

p A′( p )

−

e T .

На рис. 3.8, б приведена переходная характеристика звена.

Она спадает по экспоненте до нуля от значения h(0) = k . На

рис. 3.8, в приведена реализация реального дифференцирующего звена на операционном усилителе. Для такой схемы

вх

( p) = R

R1Cp +1

, Z

ос

( p) = R .

Передаточная функция

W ( p) = −

= −

R2Cp

= −

R1Cp +1

R Cp +

Tp +1

где k = R2C ,

T = R1C .

G(ω)

h(t)

+20дБ/дек

lg ω

ϕ(ω

)

lg ω

− π

Рис. 3.8 — ЛАЧХ и ЛФЧХ (а), переходная характеристика (б) реального дифференцирующего звена и его реализация

на операционном усилителе (в)

3.2.2 Звенья второго порядка

В общем случае звено второго порядка описывается уравнением

T	d 2 y(t)		+T	dy(t)	+ y(t) = kx(t) ,

1 dt		2	2	dt

или в операторной форме записи

(T12 p2 +T2 p +1)Y ( p) = kX ( p).

Отсюда определяем передаточную функцию:

W ( p) =		k		(3.1)
			.
	T 2 p2	+T p +1
1		2

В зависимости от характера полюсов передаточной функции (3.1) (корней уравнения T12 p2 +T2 p +1 = 0 ) различают апе-

риодическое звено второго порядка, колебательное и консервативное звенья.

3.2.2.1 Апериодическое звено второго порядка

Это звено имеет место при отрицательных вещественных полюсах передаточной функции (3.1), которую в этом случае можно представить в виде:

W ( p) =		k	=	k
					,	(3.2)
	T 2 p2	+T p +1		(T3 p +1)(T4 p +1)
1		2

где эквивалентные постоянные времени T3, T4 рассчитываются по соотношению

	T		T 2		2 .
T =	2	±	2	−T		(3.3)

3,4	2		4	1

Анализируя выражение передаточной функции (3.2), можно сделать вывод о том, что апериодическое звено второго порядка состоит из двух инерционных (апериодических) звеньев с эквивалентными постоянными времени T3, T4 , поэтому логарифми-

ческие частотные характеристики этих инерционных звеньев складываются.

На рис. 3.9, а показаны ЛАЧХ и ЛФЧХ апериодического

звена второго порядка. До частоты сопряжения ωc1 = 1 ЛАЧХ

горизонтальна на уровне G0 = 20lg k , после этой частоты до

					65
частоты сопряжения ω				= 1	имеет наклон –20 дБ/дек, а после
		c2		T3
				T3
ωc2 проходит с наклоном –40 дБ/дек. ЛФЧХ асимптотически
приближается к значению −π.
G(ω)		–20дБ/дек
G0			–40дБ/дек
0	lg 1	lg 1			lg ω
ϕ(ω)	T3	T4			h(t)
ϕ(ω)
					k
0					lg ω
− π
4
− π
2
− 3
4					0	t
− π					0	t
− π		а			б
					б

Рис. 3.9 — ЛАЧХ и ЛФЧХ (а), переходная характеристика (б)
		апериодического звена второго порядка

По формуле (2.14) получим расчетное выражение для переходной функции апериодического звена второго порядка. Для него

B( p) = B = k ,

A( p) =(T3 p +1)(T4 p +1) ,

p = −

, тогда

h(t) =

B(0)

B( p )e p1t

B( p )e p2t

A(0)

p1A′( p1)

p2 A′( p2 )

= k 1

T4 −T3

A′( p) = 2T3T4 p +T3 +T4 ,

−	t		T4		−	t
e T3 +			T4	e		T4 .
e T3 +			−T3	e		T4 .
		T4	−T3

Переходная характеристика звена показана на рис. 3.9, б, ее характерная особенность — наличие точки перегиба вследствие суммирования двух экспоненциальных составляющих.

3.2.2.2 Колебательное звено

Это звено получается при комплексных сопряженных полюсах передаточной функции (3.1). Передаточную функцию звена удобнее записывать в виде

W ( p) =				k
					,
		T 2 p2 + 2ξTp +1
где T =T , а параметр	ξ =		T2	называется		коэффициентом

1			2T1

демпфирования. Для колебательного звена						0 < ξ <1. Можно

также отметить, что при ξ ≥1 полюсы передаточной функции

(3.1) становятся вещественными и звено будет апериодическим второго порядка.

Получим формулы для частотных характеристик колебательного звена:

W ( jω) =

k (1−ω2T 2 −2 jξωT )

1−ω2T 2 + 2 jξωT

(1−ω2T 2 )2 + 4ξ2ω2T 2

P(ω) = k

1−ω2T 2

(1−ω2T 2 )2 + 4ξ2ω2T 2

Q(ω) = −k

2ξωT

(1−ω2T 2 )2 + 4ξ2ω2T 2

A(ω) =

W ( jω)

(1−ω2T 2 )2 + 4ξ2ω2T 2

G(ω) = 20lg k −20lg

(1−ω2T 2 )2 + 4ξ2ω2T 2 ,

			67
	ϕ(ω) = arctg Q(ω) = −arctg			2ξωT		.
		P(ω)		1−ω2T 2
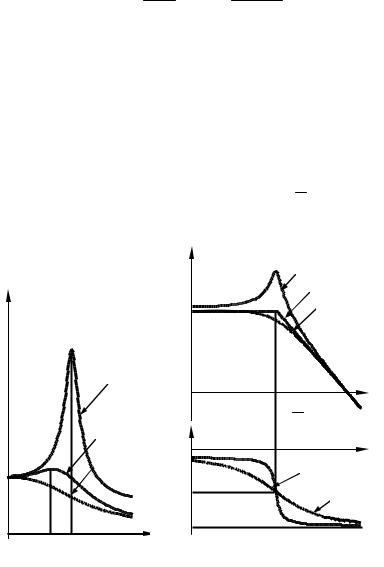
Частотные характеристики колебательного звена приведены
на рис. 3.10. Они существенно зависят от величины коэффици-
ента демпфирования ξ. При 1 > ξ > 0,707 АЧХ A(ω) (рис. 3.10, а)
монотонно уменьшается с увеличением частоты. При ξ < 0,707
на ней появляется «горб», который увеличивается по мере
уменьшения ξ. На ЛАЧХ (рис. 3.10, б) «горб» проявляется при
ξ < 0,5 , при больших значениях коэффициента демпфирования
ЛАЧХ приближается к ее асимптотическому варианту (имеет
нулевой	наклон	до частоты сопряжения			ω = 1		и	наклон
					c	T
–40дБ/дек после этой частоты).						T
–40дБ/дек после этой частоты).
			G(ω
						ξ < 0,5
A(ω)						–40 дБ/дек
A(ω)			G				ξ > 0,5
		ξ → 0
					lg 1			ω
					lg 1
		ξ < 0,707	ϕ(ω)			T
		ξ < 0,707	ϕ(ω)
k		ξ > 0,707				ξ < 0,5		lgω
k			− π				ξ > 0,5
			− π				ξ > 0,5
			2
			−π
0	ωк1 ωк2	ω			б
	а				б
Рис. 3.10 — Частотные характеристики колебательного звена

Величина «горба» на частоте				ω	=	1	1− 2ξ может быть
Величина «горба» на частоте				ω	=		1− 2ξ может быть
оценена по соотношению [6]:				к		T
оценена по соотношению [6]:
H = 20lg		1		≈ 20lg			1	.
H = 20lg				≈ 20lg				.
	2ξ	1−ξ	2				2ξ
	2ξ	1−ξ

Переходная функция колебательного звена может быть получена по формуле (2.14) при комплексных сопряженных полю-

сах

−ξ±

ξ2

−1

ξ <1

выражение ξ2 −1 становится

(при

1,2

меньше нуля):

ξ t

1−ξ

h(t) = k

−e

− T

t +

. (3.4)

cos

1−ξ

sin

На рис. 3.11 показаны переходные характеристики колебательного звена, рассчитанные по выражению (3.4) для различных значений коэффициента демпфирования ξ. Частота собст-

венных колебаний переходной характеристики оценивается по

выражению ω =	1−ξ2	и равна мнимой части полюсов p .

к	T	1,2

Ее можно также определить и по АЧХ (см. рис. 3.10, а, частоты ωк1 и ωк2 , соответствующие максимальным значениям на АЧХ). Огибающая (см. пунктир на рис. 3.11) определяется фор-

−ξt

мулой h0 (t) = ke T . Время переходного процесса на практике оценивается соотношением

tпп ≈ 3ξT .

Примером звена второго порядка может служить колебательный контур (см. схему на рис. 2.6 и вывод передаточной функции в примере 2.5).

h(t

ξ = 0,15 ξ = 0,7

hmax

Рис. 3.11 — Переходные характеристики колебательного звена

Пример 3.2

Определить, при каком соотношении параметров элементов схемы колебательный контур (см. рис. 2.6) является колебательным звеном.

Запишем полученную в примере 2.5 передаточную функцию с использованием коэффициента демпфирования:

W ( p) =

+ R2

R2LC

R1R2C + L

2 p2

p2 +

p +1 T

+ 2ξTp +1

+ R

Отсюда выразим коэффициент демпфирования:

R1R2C + L

= 2ξT;

R1 + R2

ξ =

R1R2C + L

2T (R1 + R2 )

2(R1

+ R2 )

R LC

2 (R + R

)R LC

R1 + R2

Звено будет колебательным, если ξ <1, т.е.

R1R2C + L

< 2 .

(R1 + R2 )R2LC

<<< < Предыдущая 1 2 3 4 5 67 / 177 8 9 10 11 12 13 14 15 16 17 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.20231.66 Mб17Теория автоматического управления.-3.pdf
#
05.02.2023961.62 Кб9Теория автоматического управления.-4.pdf
#
05.02.2023661.41 Кб7Теория автоматического управления.-5.pdf
#
05.02.2023528.41 Кб9Теория автоматического управления.-6.pdf
#
05.02.2023760.21 Кб9Теория автоматического управления.-7.pdf
#
05.02.20231.36 Mб11Теория автоматического управления..pdf
#
05.02.2023770.68 Кб22Теория автоматов и формальных языков..pdf
#
05.02.2023314.52 Кб17Теория алгоритмов и математическая логика..pdf
#
05.02.2023725.19 Кб17Теория вероятностей и математическая статистика.-1.pdf
#
05.02.2023469.85 Кб15Теория вероятностей и математическая статистика.-2.pdf
#
05.02.2023722.49 Кб14Теория вероятностей и математическая статистика.-3.pdf