
Цифровая обработка сигналов. Часть 1
.pdf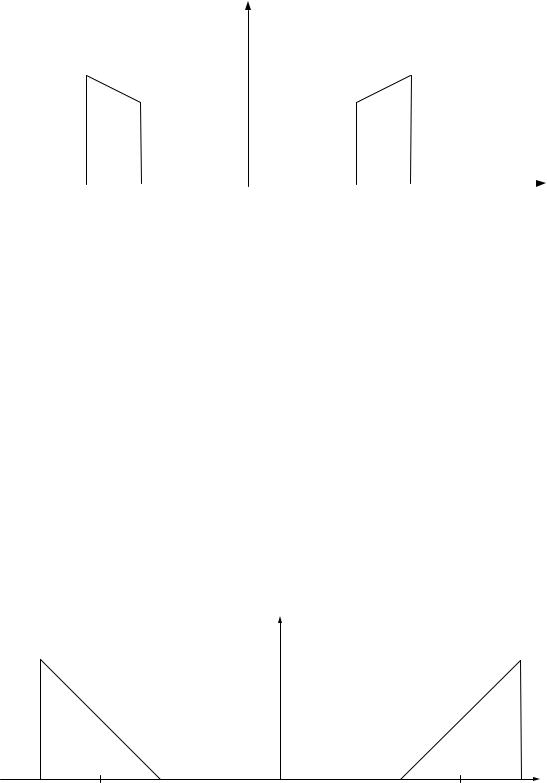
X(f)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-30 |
-20 |
-10 |
0 |
10 |
20 |
30 |
Частота (МГц) |
||||||||
Рисунок 1.26
15.1 Кратко объясните принцип полосовой дискретизации с недостаточной выборкой. Прокомментируйте преимущества применения этого метода на практике.
1. Цифровой радиоприемник на втором этапе работает на промежуточной частоте 50 кГц.
А. Найдите минимальную частоту дискретизации Fs, позволяющую избежать наложения спектров в этой системе, если ширина полосы промежуточной частоты сигнала равна 6 кГц.
Б. Изобразите спектр дискретного сигнала в интервале ±FS. Объясните, как вы получили спектр дискретного сигнала и прокомментируйте его вид.
Пусть используется метод целочисленной дискретизации и спектр сигнала на втором этапе промежуточной частоты выглядит так, как показано на рисунке 1.27.
X(f)
-50 |
0 |
50 |
f(кГц) |
Рисунок 1.27
16. На рисунке 1.28, а изображен спектр сигнала на втором этапе обработки в цифровом приемнике (преобразование на промежуточную частоту), где промежуточная частота равна 2,976 МГц. С помощью соответствующих схем покажите, что сигнал промежуточной частоты можно
41
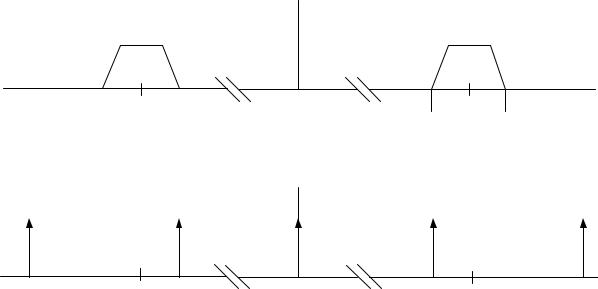
дискретизировать без наложения с частотой 128 кГц.
С помощью соответствующих схем покажите, что если промежуточная частота сигнала будет равна 3 МГц, то появится наложение, если сигнал на промежуточной частоте дискретизирован с частотой 128 МГц.
X(f)
-2,976 |
0 |
|
2,976 |
|
Частота (МГц) |
2,944 |
3,008 |
а)
P(f)
-3,072 |
-2,944 |
0 |
2,944 |
3,072 |
|
|
Частота (МГц) |
|
|
б)
Рисунок 1.28. Спектр сигнала на втором промежуточном этапе (панель а); спектр выборочной функции (панель 6)
17. Запишите уравнение, выражающее теорему о полосовой дискретизации. Объясните, почему теорема о полосовой дискретизации представляет интерес для цифровой связи.
Из записанного уравнения выведите выражение для теоретической минимальной частоты дискретизации полосового сигнала. Предположите, что отношение верхнего края полосы частот к ширине полосы сигнала равно целому числу. Объясните, почему теоретическая минимальная частота дискретизации может оказаться непригодной на практике.
2.3 Шум квантования при аналого-цифровом преобразовании
18.В системе ЦОС реального времени используется 16-битовый АЦП в биполярном режиме с входным диапазоном ± 5 В. Какова максимальная ошибка квантования? Рассчитайте теоретическое максимальное отношение сигнал-шум квантования (в децибелах) для этой системы.
19.Синусоидальный сигнал с удвоенной амплитудой 5 В оцифровывается с помощью 16-битового АЦП. Предположив, что квантование линейно, найдите:
42
а) величину шага квантования;
б) среднеквадратическое отношение сигнал-шум квантования.
Укажите все сделанные предположения.
20.Аналоговый вход системы ЦОС оцифровывается с частотой 100 кГц при однородном квантовании. Предполагая, что на вход подается синусоидальный сигнал с удвоенной амплитудой ± 5 В, найдите минимальное число битов АЦП, позволяющее достигать отношения сигналшум квантования не менее 90 дБ. Перечислите все сделанные предположения.
21.Покажите, что отношение сигнал-шум квантования линейного АЦП задается как
SNR(q) 6,02B 4,77 20log( A / x )(дБ),
где В — количество битов АЦП, ±А — входной диапазон АЦП, а ах — среднеквадратическое значение входного сигнала. Найдите отношение сигнал-шум квантования, если разрешение АЦП равно 16 бит, а вход имеет вид:
а)синусоидального сигнала;
б)сигнала со среднеквадратическим значением А/4.
Укажите все сделанные предположения.
22. Среднеквадратическое значение аналогового входного сигнала В- битового АЦП равно σх (В). Входной диапазон АЦП подходит для значений в пределах ± 3σх (В). Найдите выражение для отношения сигнал-шум квантования (в децибелах) преобразователя. Укажите все сделанные предположения.
2.4 Выборка с запасом по частоте при аналого-цифровом преобразовании — наложение спектров и контроль за уровнем шума квантования
23. С помощью подходящих схем объясните принцип метода выборки с запасом по частоте и его использование для увеличения эффективной разрешающей способности аналого-цифрового преобразователя, работающего на частоте Найквиста.
В цифровой системе записи и воспроизведения звука для оцифровки аналогового входного сигнала с частотными компонентами в диапазоне 0-4
43

кГц используется метод выборки с запасом по частоте и 8-битовый биполярный преобразователь, работающий на частоте Найквиста. Оцените эффективную разрешающую способность (в битах) преобразователя, если частота дискретизации равна 40 МГц. Покажите, как вы получили этот ответ. Прокомментируйте практические проблемы, возникающие в связи с этим методом.
24. 1.Универсальная многоканальная (до 64 каналов) система сбора данных должна собирать медицинские данные. Каждый аналоговый канал должен задаваться пользователем отдельно, чтобы граничная частота его полосы пропускания была между 0,5 и 200 Гц, а выбираемая частота дискретизации — в диапазоне от 1 Гц до 2 кГц. Максимально допустимая неравномерность в полосе пропускания равна 0,5 дБ, а зеркальные компоненты должны быть как минимум на 40 дБ ниже, чем компонент сигнала.
Объясните стратегию, выбранную для удовлетворения вышеизложенным требованиям. Ответ должен включать следующие пункты:
а) рассуждения о вопросах, специфичных для данного приложения;
б) указания, как использовать в этом приложении методы дискретизации с запасом по частоте, чтобы наиболее эффективно и экономно удовлетворить данные условия (применяйте расчет цены/числа компонентов).
2. Пусть для всех каналов системы из п.1 используются идентичные фильтры защиты от наложения спектров, каждый из которых имеет следующую характеристику типа Баттерворта:
A( f ) |
1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
1 ( |
|
f |
)6 |
||
|
|
||||
|
|
|
|||
|
|
|
|
fc |
|
где /с = 3 дБ — частота среза фильтра.
3. Изобразите спектры данных до и после дискретизации и определите:
а) частоту среза fс;
б) подходящую общую частоту дискретизации Fs.
Ответ прокомментируйте.
25. Система записи и воспроизведения звука работает с сигналами, основная полоса частот которых занимает диапазон 0-20 кГц. Найдите коэффициент перевыборки и минимальную частоту дискретизации, которая
44
необходима для достижения с 8-битовым преобразователем того качества, которого можно было бы достичь с 16-битовым преобразователем.
26. 1. Напишите краткое резюме по каждому из перечисленных ниже методов для однобитового АЦП:
а) выборка с запасом по частоте;
б) ограничение спектра шума.
2.Почему в высококачественных системах ЦОС предпочтительнее однобитовые АЦП, а не обычные АЦП с достаточной аппроксимацией?
3.Для оцифровки аналогового сигнала в системе цифровой обработки сигналов с аналоговым звуковым входом в диапазоне 0-20 кГц применяется метод дискретизации с запасом по частоте и сигма-дельта-модулятор первого порядка, изображенный на рисунке 1.29. Предположив, что частота дискретизации равна 3,072 МГц, найдите характеристику фильтра ограничения шума при 20 кГц. Оцените эффективную разрешающую способность (в битах) устройства оцифровки.
|
x(t) |
Фильтр |
|
|
y(n) |
||
|
|
Σ |
|
ограничения |
|
1-битовый АЦП |
|
|
|
|
шума первого |
|
|
||
Аналоговый |
|
|
|
||||
|
вход |
порядка |
|
|
|
||
1-битовый ЦАП |
|
Единичная |
|
|
задержка |
|
|
|
|
|
Рисунок 1.29. Сигма-дельта-модулятор первого порядка
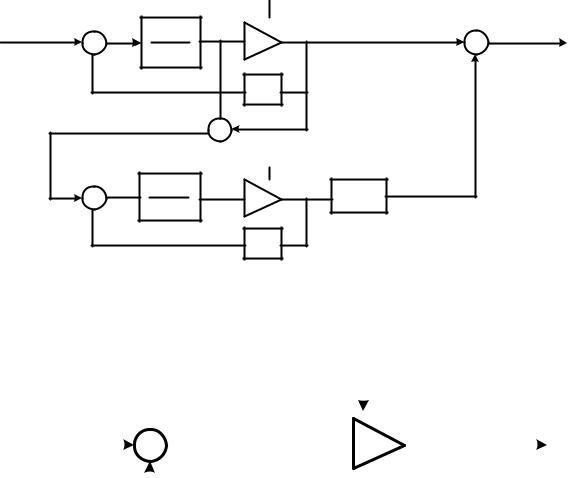
27. В системе цифровой обработки сигналов с аналоговым звуковым входом в диапазоне 0-20 кГц для преобразования аналогового сигнала в цифровой поток битов с частотой 6,144 МГц применяется метод выборки с запасом по частоте и сигма-дельта-модулятор второго порядка. На рисунке 1.30 изображена модель сигма-дельта-модулятора на z-плоскости.
Определите общее улучшение отношения сигнал-шум квантования, которое становится возможным благодаря дискретизации с запасом по частоте и ограничению шума, и оцените эффективную разрешающую способность (в битах) устройства оцифровки.
28. В системе цифровой обработки сигналов с аналоговым звуковым входом в диапазоне 0-20 кГц для преобразования аналогового сигнала в цифровой поток битов с частотой 6,144 МГц применяется метод выборки с
45
запасом по частоте и сигма-дельта-модулятор первого порядка. На рисунке
1.31изображена модель сигма-дельта-модулятора на z-плоскости.
1.Объясните, как цифровой поток битов можно преобразовать в цифровой многобитовый поток с частотой 92 кГц.
2.Найдите общее улучшение отношения сигнал-шум квантования, которое становится возможным благодаря дискретизации с запасом по частоте и ограничению шума, и оцените эффективную разрешающую способность (в битах) устройства оцифровки.
|
|
Интегратор |
|
|
E1 |
|
|
|
|
|
|
|
|
Аналоговый |
|
1 |
P1 |
|
C1 |
Цифровой |
|
|
|
|
|||
X |
Σ |
1-z -1 |
|
|
Σ |
Y |
вход |
|
|
|
|
выход |
|
|
|
|
|
- |
z -1 |
|
|
|
|
|
|
|
|
|
|
|
Σ |
|
|
|
|
|
Интегратор |
|
|
E2 |
|
|
|
1 |
P2 |
|
C2 |
|
- |
Σ |
1-z -1 |
|
|
1-z -1 |
|
|
|
|
|
|||
|
|
|
|
|
||
|
|
|
|
|
Дифференциатор |
|
|
|
|
|
|
z -1 |
|
Рисунок 1.30. Результат преобразования Y(z) на выходе сигма-дельта- модулятора второго порядка задается как Y (z) X(z) E2 (z)(1 z 1 )2
|
|
|
|
|
Интегратор |
|
|
|
E(z) |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
+ |
|
|
|
|
|
|
|
P1 |
Цифровой |
||||||
|
Аналоговый |
|
|
|
1 |
|
|
||||||||||
|
|
|
|
|
|
|
|||||||||||
x(z) |
Σ |
|
|
|
|
|
|
|
|
|
|
|
|
||||
вход |
- |
|
|
1-z -1 |
|
|
|
|
|
|
|
выход |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
(0-20 кГц) |
|
|
|
|
|
|
|
|
|
|
|
|
|
(6,144 МГц) |
|||
|
|
|
|
|
|
|
|
Компаратор |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z -1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 1.31. Модель сигма-дельта-модулятора на я-плоскости
2.5 Цифроаналоговые преобразования и эффект sin х/х
29. На рисунке 1.32, а показана блок-схема системы ЦОС реального времени со аналоговым выходом, а на рисунке 1.32, б изображена основная полоса частот спектра сигнала, который подается на ЦАП. Изобразите спектр
46

сигнала на выходе ЦАП в интервале от 0 до 2Fs, где Fs — частота дискретизации. Найдите амплитуды компонентов сигнала, учитывая, что частота дискретизации равна 15 кГц.
30. В системе ЦОС реального времени используется 16-битовый процессор, 12битовый АЦП с временем преобразования 15 мкс и 12битовый ЦАП со временем установки сигнала 500 не. Необходимая операция ЦОС — это сверточное суммирование, которое задается как
N 1
y(n) h(k)x(n k),
k 0
где переменные имеют обычные значения, а вычисления должны выполняться между элементами выборки. Оцените пропускную способность системы в реальном времени, указав все сделанные предположения.
Система |
|
|
y(n) |
|
|
ЦАП |
|
y (n) |
ЦОС |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задержка нулевого порядка |
|||||
|
|
|
|
|
а) |
|||
|Y(f)| |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
||
|
|
|
|
3 |
|
|
||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
Частота (кГц) |
б)
Рисунок 1.32. Система ЦОС реального времени с аналоговым выходом (панель а); спектр сигнала, который подается на ЦАП (панель б)
31. Выход цифроаналогового преобразователя задается как реакция на цифровую последовательность:
y(t) y(n)h(t nT ),
n
где h(t) — это импульсная характеристика ЦАП, а 1/Т — скорость подачи данных на ЦАП. Пусть ЦАП имеет задержку нулевого порядка, a h(t)
— квадрат импульса длительностью T(s).
47
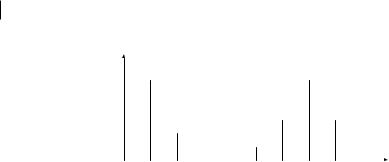
Изобразите выход ЦАП как реакцию на входную последовательность у(п), показанную на рисунке 1.33. Покажите, что действие спектрального ограничения ЦАП на спектр сигнала можно компенсировать с помощью цифрового фильтра, спектр которого имеет вид
H ( ) |
|
|
T |
|
|
|
. |
||
|
2sin(T / 2) |
|||
|
|
|
||
|
|
|
y(n) |
|
4
|
|
|
|
|
|
0 |
2 |
|
6 |
8 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 1.33.
32.Критически оцените основные ограничения и ошибки, возникающие
впроцессе аналогового/цифрового преобразования в системах цифровой обработки сигналов реального времени, и подумайте о том, как можно уменьшить каждую из этих ошибок и снизить влияние ограничивающих факторов.
2.6 Выборка с запасом по частоте в цифроаналоговом преобразовании: контроль за зеркальными частотами и шумом квантования
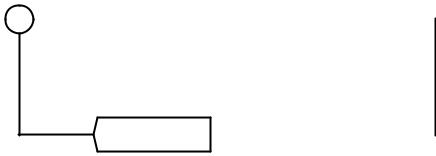
33. На рисунке 1.34 изображено устройство, которое используется для восстановления аналогового сигнала после того, как он был обработан определенной цифровой системой записи и воспроизведения звука, работающей в реальном времени. Основная полоса частот аналогового сигнала простирается от 0 до 24 кГц, а частота дискретизации равна 192 кГц.
Зеркальные частоты следует приглушать как минимум на 50 дБ, чтобы при этом компоненты звукового сигнала не подавлялись больше, чем на 0,5 дБ. Воспользовавшись соответствующими изображениями спектра сигнала, найдите минимальные значения порядка и частоты среза фильтра подавления зеркальных частот, предположив, что он имеет характеристику типа Баттерворта. Перечислите все сделанные предположения.
48
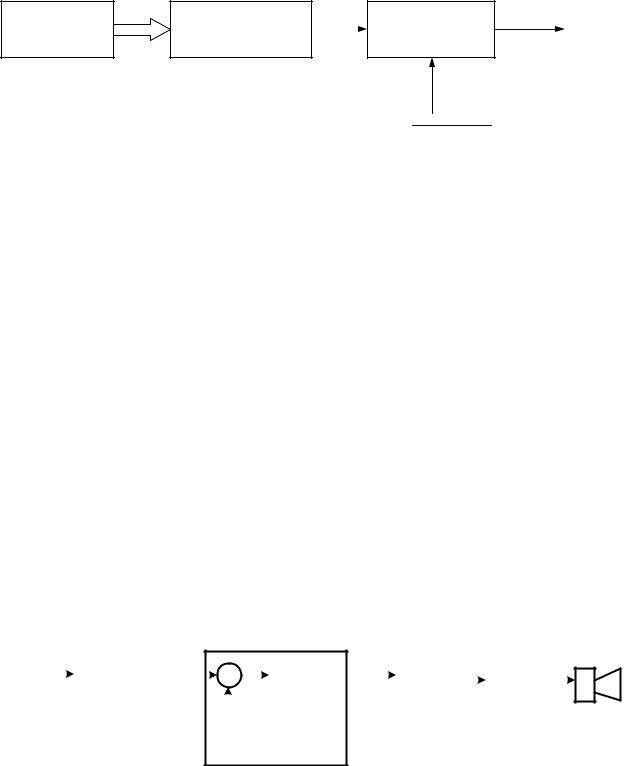
Цифровой |
Цифроаналоговый |
|
Фильтр подавления |
процессор |
преобразователь |
|
зеркальных частот |
Аналоговый
выход
|H(f)|= 1 [1+(f/fC)2]1/2
Рисунок 1.34. Выходной каскад системы ЦОС реального времени
34. На рисунке 1.35 изображено устройство, которое используется для восстановления аналогового сигнала после обработки цифровой системой записи и воспроизведения звука, работающей в реальном времени. Основная полоса частот аналогового сигнала простирается от 0 до 20 кГц, а частота дискретизации равна 176,4 кГц.
Ограничитель шума описывается следующими уравнениями:
y '(n) x(n) e(n 1), |
e(n) y(n) y '(n). |
1.Выведите выражение для передаточной функции, которая действует на шум квантования, а затем изобразите спектр шума квантования после ограничения шума.
2.Найдите улучшение отношения сигнал-шум квантования, возможность которого дает выборка с запасом по частоте и ограничение шума, а затем оцените эффективную разрешающую способность ЦАП (в битах). Предположите, что осуществляется четырехкратная выборка с запасом по частоте.
|
|
|
Фильтр для |
176,4 кГц |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
выборки с |
|
|
Q |
|
|
|
|
|
14-битовый |
|
|
Аналоговый |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Цифровой |
запасом по |
x(n) |
|
|
|
|
|
|
|
y(n) |
|
|
|
||||||
|
|
|
|
|
|
|
|
ЦАП |
|
|
ФНЧ |
|
|||||||
частоте |
(28 бит) |
|
|
|
|
|
|
|
|
|
|
|
|||||||
вход |
|
|
|
|
|
|
|
|
(14 бит) |
|
|
|
|
|
|||||
(44,1 кГц) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
z-1 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
e(n-1) |
|
e(n) |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
Ограничитель шума |
|
|
|
|
|
|
|
|||||||
Рисунок 1.35. Упрощенная блок-схема воспроизведения звукового сигнала проигрывателем компактдисков с четырехкратной выборкой с запасом по частоте и ограничением формы шума
35.Системе ЦОС предшествует устройство дискретизации с задержкой
сапертурным временем 10 не и временем детектирования 1 μ с, за которым
49
идет 8-битовый АЦП. Найдите максимальное время преобразования АЦП, которое поддерживает частоту дискретизации 100 кГц.
2.7 Задачи для решения с помощью Scilab
36. На рисунке 1.35 изображено устройство, которое используется для восстановления аналогового сигнала после обработки цифровой системой записи и воспроизведения звука реального времени. Основная полоса частот аналогового сигнала расположена от 0 до 20 кГц, а частота дискретизации равна 176,4 кГц.
1.С помощью Scilab рассчитайте и постройте график спектра удобного фильтра четырехкратной выборки с запасом по частоте с КИХ. Укажите коэффициенты этого фильтра.
2.Представьте коэффициенты фильтра в виде 12-битовых чисел с фиксированной запятой.
3.Сгенерируйте звуковой сигнал (16-битовый при частоте 44,1 кГц).
4.Создайте в Scilab модель цифроаналогового процесса, пользуясь арифметикой с фиксированной запятой, и постройте график сигнала на выходе каждого блока в частотных и временных координатах.
37. На рисунке 1.36, а изображен спектр сигнала в системе связи с шириной полосы В и несущей частотой fс. Аналоговый сигнал проходит через фильтр защиты от наложения спектров и дискретизируется с частотой Fs. Искомый спектр дискретного сигнала изображен на рисунке 1.36, б.
1. Предоставьте спецификацию подходящего фильтра защиты от наложения спектров и обоснуйте свое решение.
2. Назовите подходящие частоты дискретизации, которые позволят восстановить спектр на рисунке 1.36, б без наложения. Изобразите спектр, полученный в каждом случае.
3. Чтобы частота дискретизации была как можно ниже, выберите наименьшую частоту дискретизации из п. 2 и проверьте спектр повторно дискретизированного сигнала с помощью пакета Scilab. Приведите в ответе код Scilab.
Подсказка. Дискретизация — это умножение во временных координатах, что математически равнозначно свертке в частотных координатах. Возьмите частотный спектр выборочной функции и выполните его свертку со спектром на рисунке 1.36, а.
50
