
Сборник задач для студенческих олимпиад по математике
..pdf
ЗАДАЧА 11. (Геометрия + математический анализ (экстремум)) Найти такое отношение высоты к радиусу основания конуса, чтобы при фиксированном объѐме площадь боковой поверхности конуса была минимальна.
Справка. Площадь боковой поверхности конуса вычисляется по формуле Rl , где l - длина боковой образующей.
РЕШЕНИЕ. Объѐм конуса V 13 Sh = 13 R2h , боковая образующая
вычисляется по теореме Пифагора: l 
 R2 h2 . Найти экстремум величины Rl при фиксированном объѐме V. Сначала выразим
R2 h2 . Найти экстремум величины Rl при фиксированном объѐме V. Сначала выразим
|
3V |
|
|
2 |
3V |
2 |
|
высоту через R: h |
|
. Тогда l |
R |
|
|
|
. |
R2 |
|
R2 |
|||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
3V |
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
9V 2 |
|
|
2 R6 9V 2 |
|
||||||||||||||
Rl = R R |
|
|
|
|
|
|
|
|
|
|
= R R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= R |
2 R4 |
= |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 R4 |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
R |
|
|
2 R6 9V 2 |
|
|
|
2 R6 9V 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
R2 |
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Найдѐм условие, при котором производная по R равна 0. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6R5 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R 2 R6 9V 2 |
|
|||||||||||||||||||||||||
|
|
|
|
|
R |
|
9V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
2 |
6 |
2 |
|
|
2 |
|
|
|
2 |
R |
6 |
9V |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R2 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
3R5 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
R 2 R6 9V 2 , 3R6 2 2 R6 9V 2 , |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
2 R6 |
9V 2 |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2R6 2 9V 2 , R6 |
|
9 V 2 |
, R 6 |
9 |
3 |
|
|
V |
. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
2 2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Замечание. Можно также убедиться, что получили минимум, а не максимум. Для этого установим тот факт, что вторая производная по параметру R положительна.
21

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 R6 9V 2 |
1 |
|
|
|
3R6 2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
2 R6 9V 2 |
= |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
R |
|
|
|
R |
2 |
|
|
2 |
R |
6 |
9V |
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
18R5 2 |
2 R6 9V 2 |
|
|
|||||||||
= |
|
2 R6 9V 2 3R6 2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
2 |
|
|
2 |
R |
6 |
|
9V |
2 |
|
||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
6 2 R5 |
||
|
|
|
|
|
, что в итоге сводится к выражению |
|
R2 |
|
|
|
|||
|
|
|
||||
|
|
2 2 R6 9V 2 |
||||
|
1 18R |
|
|
|
|
|
R |
|
|
9V |
|
3 |
|
R |
|
|
|
3R |
|
|
|
|
|
|
|
|
3 |
|
R |
|
|
|
|
R |
|
9V |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
5 |
|
|
6 |
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
5 |
|
|
|
|
|
2 |
|
|
6 |
|
|
|
|
2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
||||
|
R2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
R |
6 |
|
9V |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
R |
6 |
|
9V |
2 |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|||||||||||||||||||||||||||||||||
множим на положительную величину R2 |
|
|
|
2 R6 9V 2 |
, теперь |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
достаточно проверить знак выражения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
18R5 2 |
2 R6 9V 2 |
|
3 2 R5 3R6 2 3 2 R5 2 R6 9V 2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
После приведения подобных получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
3 2 R5 (2R6 2 45V 2 ) >0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Подставим найденное выражение R 6 |
|
|
9 |
3 |
|
|
V |
|
|
|
в h : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
h |
|
|
3V |
|
|
= |
|
|
|
|
|
|
|
|
|
3V |
|
|
|
|
|
|
|
|
|
. Найдѐм соотношение |
|
|
h |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
R2 |
|
|
|
|
|
|
|
|
9 |
|
|
|
|
V |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
3V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
3V |
|
|
|
|
|
|
|
|
|
|
|
3V |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
= 2 . |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 V |
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
9 |
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
6 |
3 |
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
6 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
ОТВЕТ: |
|
|
|
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
22
ЗАДАЧА 12. (Геометрия + математический анализ (экстремум)) Найти, какую максимальную долю объѐма может занимать прямой круговой конус, вписанный в шар радиуса R .
РЕШЕНИЕ. |
|
|
|
|
Объѐм шара равен, как известно, |
4 |
R3 |
. Для вписанного в шар |
|
3 |
||||
|
|
|
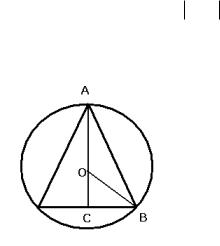
конуса, высота h и радиус r взаимосвязаны между собой. Расстояние от центра основания конуса до центра шара есть h R (см.чертѐж -
вид сбоку, на чертеже это ОС). Отрезок ВС на чертеже равен r -
радиусу основания конуса. Далее, по теореме Пифагора (ОС)2+(ВС)2 =
(ОВ)2.
То есть, |
(h R)2 r 2 |
R 2 , следовательно, |
|
(h R)2 r 2 |
R 2 , |
|||||||||||||
r 2 R 2 (h R)2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
r 2 R 2 |
(h2 R 2 2Rh) , |
r 2 2Rh h2 . По известным |
||||||||||||||||
формулам, объѐм конуса равен V |
1 |
Sh , а |
площадь основания |
|||||||||||||||
3 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
S r 2 , тогда V |
1 |
|
r 2 h , |
V |
1 |
|
(2Rh h2 )h = (2Rh2 h3 ) . |
|||||||||||
|
|
|
|
|
||||||||||||||
|
|
3 |
|
3 |
|
|
|
3 |
|
|
||||||||
Найдѐм экстремум по h . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
2 |
) 0 , 4Rh 3h |
2 |
|
4 |
|
|
|
||||||||
V (h) |
3 (4Rh 3h |
|
|
|
, h |
|
|
R . |
|
|
||||||||
|
|
|
|
3 |
|
|
||||||||||||
Легко убедиться, что это именно максимум, так как вторая |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
(4R 6h) , при h |
4 |
|
||||||
|
|
|
|
|
|
|
|
|
|
3 R |
||||||||
производная отрицательна: V |
(h) |
3 |
||||||||||||||||
23

|
|
|
4 |
|
|
|
|
4R 6 |
|
R = 4 |
|
R 0 . |
|
получается V (h) |
|
|
|
|||
|
3 |
|
3 |
|
3 |
|
При этом значении объѐм конуса равен V |
1 |
r 2 h = |
|||||||||||||||||||
3 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
2 |
|
4 |
|
1 |
|
4 |
|
16 |
|
|
2 |
|
4 |
|
|
|||
V |
|
(2Rh h |
|
) |
|
R = |
|
2R |
|
R |
|
|
R |
|
|
|
|
R |
= |
||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
3 |
|
|
|
3 |
|
3 |
|
3 |
|
9 |
|
|
|
|
|
3 |
|
|
||
4 |
R |
3 |
|
8 |
|
16 |
4 |
R |
3 |
8 |
|
32 |
R |
3 |
|
|
|
|
|
|
|
= |
|
|
|
= |
|
|
. |
||||
|
|
|
|
|
|
|
|
|
||||||||
9 |
|
|
|
3 |
|
9 |
9 |
|
|
9 |
|
81 |
|
|
|
|
Нужно найти отношение объѐма конуса к объѐму шара, поэтому |
|
|
||||||||||||
поделим друг на друга объѐмы этих тел: |
32 |
R3 |
: |
4 |
R3 |
= |
32 |
|
|
3 |
= |
|||
81 |
3 |
81 |
4 |
|||||||||||
|
|
|
|
|
|
|
|
|
||||||
|
8 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
27 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
ОТВЕТ. Максимальная доля объѐма, занимаемая вписанным конусом в шаре, 278 .
24

ЗАДАЧА 13. (Геометрия + математический анализ (экстремум))
На плоском листе нарисован график функции sin 2 t , затем лист свѐрнут в цилиндр радиуса 1 вокруг оси Z так, чтобы совпали точки, отличающиеся на 2 . Найти наибольший угол между касательной к получившейся пространственной кривой и плоскостью Oxy.
РЕШЕНИЕ. Пусть исходный график лежит в плоскости параметров t,u , график u sin2 t . Преобразование координат при таком переходе от плоскости параметров ( t,u ) к пространственным координатам ( x, y, z ) задаѐтся так: x cost , y sin t , z u .
Таким образом, указанная кривая переходит в пространственную кривую, заданную параметрически:
x cost , |
y sin t , |
z sin2 t . |
Касательная к пространственной |
||
кривой выражается по формуле: |
|
|
|
||
(x , y , z ) ( sin t,cost,2sin t cost) . |
|||||
Тангенс угла наклона касательной по отношению к плоскости Oxy
можем |
|
|
|
найти |
по |
формуле |
|
|
|
|
|
|
z |
|
|
= |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x ) |
|
( y ) |
|||
|
|
|
2sin t cost |
|
|
|
|
= 2sin t cost = sin 2t . |
Экстремум |
достигается |
при |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
sin 2 t cos2 t |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(sin 2t) 2cos2t |
0 2t 2 k , t 4 |
2 k . Это соответствует 4- |
|||||||||||||||||||||||||||||||
м |
|
|
касательным |
к |
пространственной |
кривой, |
а |
именно |
|
в точках |
|||||||||||||||||||||||
|
|
1 |
|
, |
1 |
|
|
1 |
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
, |
|
, |
tg угла |
наклона |
|
|
|
|
|
|
|
= sin 2t = |
1 в |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
2 |
|
2 |
|
2 |
|
|
|
2 |
|
2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x ) |
( y ) |
|
|
|
|
|
||||||
указанных точках, поэтому искомый угол 45 градусов. ОТВЕТ: 45 градусов.
25
ЗАДАЧА 14. (Геометрия + математический анализ (экстремум))
Поверхность |
z ax2 by 2 |
пересекается с прямым круговым |
цилиндром |
x2 y 2 1 . |
Найти максимальный угол между |
касательной к получившейся пространственной кривой и плоскостью
0xy.
РЕШЕНИЕ. |
|
|
Для справки, при |
ab 0 поверхность вида |
z ax2 by 2 есть |
гиперболический |
параболоид, при ab 0 |
это эллиптический |
параболоид. Для того, чтобы найти уравнения пространственной
кривой, введѐм параметр t . Так |
как |
движение в проекции |
на |
плоскость 0xy происходит по окружности, то очевидно, |
|
||
x cost , y sin t . Тогда z a cos2 t bsin 2 t . 0 t 2 . |
|
||
Вычислим направляющий вектор касательной: |
|
||
x sin t , y cost . |
|
|
|
z 2a cost( sin t) 2bsin t cost |
= |
2(a b)sin t cost |
= |
(a b) sin 2t .
Вообще, для произвольного вектора P ( A, B, C) тангенс угла
C
наклона  , тогда угол наклона к горизонтальной плоскости
, тогда угол наклона к горизонтальной плоскости
 A2 B 2
A2 B 2
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
равен |
arctg |
|
|
|
|
|
|
|
|
|
. |
В |
этой задаче |
направляющий |
вектор |
|||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
A |
2 |
|
B |
2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
sin t, cost, (a b) sin 2t |
, |
поэтому |
угол наклона |
равен |
||||||||||||||
|
(a b) sin 2t |
|
= arctg (a b) sin 2t . |
|
||||||||||||||
arctg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
sin |
2 |
t |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
t |
|
|
|
|
|
|
||||||||
В задаче требуется только абсолютное значение угла, поэтому знаком
«-» можно пренебречь. Итак, осталось найти экстремум величины |
||||||
arctg (a b) sin 2t . |
Но |
arctg |
функция монотонная, поэтому |
|||
достаточно найти |
и приравнять |
к |
0 производную только |
от |
||
(a b) sin 2t . (Впрочем, |
даже если |
вычислить |
производную |
от |
||
arctg (a b) sin 2t , |
мы |
всѐ равно получим, что |
равенство нулю |
|||
должно быть именно в числителе, и результат будет точно таким же).
26
|
= 2(a b) cos2t 0 , что возможно лишь в двух |
|
Итак, (a b)sin 2t |
||
случаях: |
|
|
1) b a , этот случай соответствует поверхности |
z a(x 2 y 2 ) - |
|
эллиптический параболоид. Для него любое горизонтальное сечение есть окружность, и угол наклона тождественно равен 0, и его максимум тоже 0.
2) cos2t 0 , при этом |
2t |
|
k , |
t |
|
|
k , что фактически |
||||
|
|
2 |
|
|
|
4 |
|
2 |
|
||
даѐт всего два разных значения: |
t |
|
и |
t |
3 |
. При этом угол |
|||||
4 |
|
4 |
|||||||||
|
|
|
|
|
|
|
|
||||
между горизонтальной плоскостью и касательной к рассматриваемой |
|||||||
кривой |
составляет |
|
arctg (a b) sin 2t , |
т.е. получаем значения |
|||
|
|
|
|
|
|
3 |
|
arctg |
(a b) sin |
|
|
и |
arctg (a b) sin |
|
, по модулю они |
|
|
||||||
|
|
2 |
|
|
|
2 |
|
одинаковы, и равны величине arctg a b . |
|
|
|||||
Ответ: Максимальный угол составляет arctg a b .
27

ЗАДАЧА 15. |
(Геометрия + математический анализ (экстремум)) |
|||
Уравнения |
движения |
точки |
заданы |
параметрически: |
x(t) t 2 , y(t) 1 t3 . |
Касательная к |
еѐ траектории отсекает |
||
треугольник в первой четверти. Найти наименьшую возможную площадь такого треугольника.
Решение. Уравнение касательной y y0 f (x0 ) (x x0 ) , а для параметрической кривой производная вычисляется так:
f (x0 ) y (t0 ) . Итак, найдѐм уравнение касательной для x (t0 )
произвольного параметра t.
y (1 t3 ) |
3t 2 |
(x t 2 ) , |
y |
3 |
tx |
3 |
t3 |
t3 1 , подставим x=0 |
|
2t |
2 |
2 |
|||||||
|
|
|
|
|
|
для поиска точки пересечения касательной с осью Oy, и y=0 для поиска пересечения с осью Ox.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Находим, что точки пересечения с координатными осями: |
0, |
|
1 |
|||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и |
|
t |
|
|
|
,0 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
3t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
t |
3 |
|
2 |
|
|
|
|
|
|
|
||
Площадь треугольника равна S |
|
|
1 |
t |
|
|
2 |
= |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
3t |
|
|
|
|
|||||||
1 |
|
3 |
|
|
|
|
2 |
|
2 |
|
|
|
1 |
|
5 |
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
t |
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
1 |
t |
|
|
|
= |
|
|
|
|
|
|
|
2t |
|
|
|
|
|
|
. Осталось найти экстремум по t. |
||||||||||||||||||
6 |
2 |
|
|
|
|
|
|
t |
|
|
|
6 |
2 |
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
5t 4 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Уравнение S (t) |
|
|
|
|
|
|
|
4t |
|
|
|
|
|
|
0 сводится к уравнению |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
2 |
|
|
|
|
|
t |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
5t6 8t3 4 0 . Обозначим t3 |
u |
и решим квадратичное уравнение |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
5u2 8u 4 0 , u 8 144 |
= 4 6 , имеет смысл только |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|||
положительное u так же как и t |
(так как при их отрицательных |
|
||||||||||||||||||||||||||||||||||||||||||
значениях треугольник находится не в первой четверти).
28
u t3 |
2 |
, t 3 |
|
2 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
5 |
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
1 |
t3 |
|
t 2 |
|
|
|
2 |
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
6 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
4 |
|
|
2 |
|
|
5 |
|
|
|||||||||||||||||||||||||||||||||
S |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
1 |
|
3 |
|
|
|
|
|
3 |
|
|
|
|
= |
|
|
|
|
||||||||||
|
|
2 |
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
2 5 |
|
|
|
3 25 3 2 |
|
|
|
2 5 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3t |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1 |
4 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
3 |
|
|
|
|
|
|
2 3 |
|
|
|
|
= |
|
|
|
3 |
|
|
|
|
|
|
|
2 3 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
3 |
|
25 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
5 |
|
|
25 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
5 |
|
|||
ОТВЕТ. Наименьшая возможная площадь равна |
|
|
3 |
|
|
|
2 3 |
|
|
. |
|
|
|
|
|
||||||||
|
5 |
|
|
|
25 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||
29
ЗАДАЧА 16. (Математический анализ) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
Доказать монотонность функции x x x |
на полуоси (0, ) . |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
РЕШЕНИЕ. |
Функция |
|
|
x x x |
рассматривается на |
полуоси |
0, . |
||||||||||||||||||||||||||||||||||||||||||||
x x x |
exx ln x |
exp ex ln x ln x . Докажем, |
что функция x ( x x ) монотонно |
||||||||||||||||||||||||||||||||||||||||||||||||
возрастает. Найдѐм производную: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f exp ex ln x ln x ex ln x ln x = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
x ln x |
|
|
|
|
|
x ln x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
x ln x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
exp e |
|
|
|
|
|
|
ln x e |
|
|
|
|
|
|
|
|
|
x ln x e |
|
|
|
ln x = |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
exp e |
x ln x |
ln x |
|
x ln x 1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
x ln x |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
ln x x |
|
|
e |
|
ln x = |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||||
exp e |
x ln x |
ln x e |
x ln x |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln x 1 ln x = |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
exp e |
x ln x |
ln x exp x ln x |
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
ln |
|
x ln x . |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Очевидно, что exp e x ln x |
ln x 0 , |
exp x ln x 0 . Осталось доказать, |
|||||||||||||||||||||||||||||||||||||||||||||||||
что |
|
1 |
|
|
ln 2 x ln x 0 , |
|
то |
|
|
|
|
|
|
есть |
ln x |
1 |
ln 2 |
x |
или |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|||||
ln |
1 |
|
1 |
|
ln 2 x (1). При |
|
x 1 неравенство |
(1) выполняется (0 1) . |
|||||||||||||||||||||||||||||||||||||||||||
x |
x |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Также заметим, что для всех x (0, ) справедливо |
|
1 |
ln 2 x 0 . |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
||||
При x (1, ) : ln |
1 |
0 , поэтому неравенство (1) выполняется. |
|
||||||||||||||||||||||||||||||||||||||||||||||||
x |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
При |
|
|
x (0,1) : |
|
|
|
значение |
|
ln |
|
1 |
|
|
|
положительно, |
|
однако |
можно |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
утверждать, что |
|
|
ln |
1 |
|
1 |
|
, так как ln t t |
t 1. Тем более, |
если |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
добавить к дроби |
|
1 |
|
заведомо положительную величину ln 2 x . Таким |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
x |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
30
