Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Сборник задач для студенческих олимпиад по математике

..pdf

Скачиваний:

108

Добавлен:

05.02.2023

Размер:

926.94 Кб

Скачать

☆

<<< < Предыдущая 12 / 62 3 4 5 6 > Следующая >>>

Тогда

(a sin )

(a a cos )

c ,

Но

при

этом

по

условию,

поэтому:

(a sin )

a cos )

Далее преобразуем это выражение, чтобы выразить .

(sin

cos

) a

cos c

2a 2 (1 cos ) c 2

4c 2

cos

arccos 1

arccos

Ответ: arccos 1

ЗАДАЧА 6. (Тригонометрия + векторная алгебра).

Вывести формулу расстояния по поверхности планеты между двумя городами, географические координаты которых ( 1, 1 ) и ( 2, 2 ) ,

где - широта (от -900 до 900), - долгота (от 00 до 3600). Планету считать идеальным шаром радиуса R.

РЕШЕНИЕ.

Найдѐм формулы перехода от декартовых координат к

географическим. Проекция на ось Oz соответствует sin	широты,
z R sin . Тогда проекция на плоскость Oxy есть R cos ,	а так как
она проецируется ещѐ на оси x,y, в итоге имеем:
x R cos cos , y R cos sin , z R sin .

(Аналогично сферическим координатам, только здесь отмеряется от экватора, а не северного полюса).

Теперь проведѐм два радиус-вектора к двум данным точкам планеты из еѐ центра.

r1 = x R cos 1 cos 1 ,	y R cos 1 sin 1 ,	z R sin 1 .
r2 = x R cos 2 cos 2 ,	y R cos 2 sin 2 ,	z R sin 2 .

Скалярное произведение равно произведению модулей на косинус

	(r , r )
	1		2

угла. Таким образом, угол равен arccos					. Также верно
		r		r
		1		2
		1		2

r1 = r2 = R , т.к. обе точки расположены на поверхности планеты.

(r1 , r2 ) =

R 2 (cos 1 cos 1 cos 2 cos 2 cos 1 sin 1 cos 2 sin 2 sin 1 sin 2 )

= R 2 (cos 1 cos 2 (cos 1 cos 2 sin 1 sin 2 ) sin 1 sin 2 ) = R 2 (cos 1 cos 2 cos( 1 2 ) sin 1 sin 2 ) .

	(r , r )
	1		2

arccos					=
		r		r
		1		2
		1		2

	2	(cos 1 cos	2 cos(	1 2 ) sin 1 sin 2 )
R
arccos					=
				2
			R

arccos cos 1 cos 2 cos( 1 2 ) sin 1 sin 2 - угол между

векторами, проведѐнными из центра планеты к двум точкам с данными географическими координатами. Чтобы найти расстояние,

нужно этот угол умножить на радиус планеты, то есть R .

В итоге L R arccos cos 1 cos 2 cos( 1 2 ) sin 1 sin 2 .

(Если угол максимален, , получается L R , половина длины окружности).

ОТВЕТ. L R arccos cos 1 cos 2 cos( 1 2 ) sin 1 sin 2 .

ЗАДАЧА 7. (Матрицы)

Найти отношение произведения всех элементов матрицы А =

1		2	2015
			к сумме всех элементов этой матрицы.
	2
	2	1

5		0	, A4	25		0	, A6	53	0
РЕШЕНИЕ. A2			, A4				, A6				Таким
	0	5			0			0	5	3
	0	5			0	25		0	5

образом, для всех чѐтных степеней ответ известен, в частности

	1007					1007	1007
A2014	5	0		.	Тогда A2015	5	2 5	и сумма
0		5				2 5	5
		1007				1007	1007
равна 4 51007 ,		а произведение 4 (51007 )4 =					4 54028 . Отношение
произведения к сумме
4 54028	=		54028	=	53021 .
4 51007	=	51007		=	53021 .
4 51007		51007

ОТВЕТ. Отношение произведения всех элементов матрицы к сумме всех элементов этой матрицы равно 53021 .

ЗАДАЧА 8. (Геометрия + векторная алгебра).

На прямой y ax при любом параметре a R есть точка, ближайшая к точке (С,0). Найти неявное уравнение кривой, которую образуют все такие точки при a R .

РЕШЕНИЕ.

Пусть точка является ближайшей к (С,0). Тогда вектор (1, a) , расположенный на прямой, перпендикулярен вектору, соединяющему точку (x, ax) с точкой (C,0) , то есть вектору

(x C, ax) . Скалярное произведение векторов (1, a)	и (x C, ax)
равно 0, то есть
x C a2 x 0. Отсюда можно найти абсциссу точки, которая
является ближайшей к указанной. (1 a 2 )x C , x		C	. Тогда
является ближайшей к указанной. (1 a 2 )x C , x	1 a 2		. Тогда
	1 a 2

y	Ca	. Это параметрические уравнения кривой. Чтобы найти
	1 a 2

неявное уравнение кривой, нужно устранить зависимость от параметра, то есть выразить a из одного уравнения и подставить во

второе.

Из первого уравнения: a 2 x C x , a2

C x

= C

C x

a 2

C x

x C x

C x

x =

C x x

C x

x тогда

y 2

(C x)x , y 2

Cx x 2 ,

y 2 x 2 Cx 0 , выделим полный квадрат:

	2		C 2	C 2			C	2	2	C 2
y		x			0	, x		y			.

			2	4			2			4

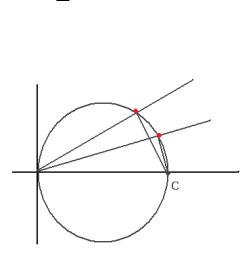
Таким образом, кривая, состоящая из точек, являющихся ближайшими

C			C
к (С,0), есть окружность с центром в точке		,0 радиуса		.
к (С,0), есть окружность с центром в точке		,0 радиуса		.
	2		2

ОТВЕТ.

радиуса

Чертѐж:

	C 2		2
x		y

	2

C2 .

C 2	C
	окружность с центром в точке		,0
	окружность с центром в точке		,0
4		2

ЗАДАЧА 9. (Геометрия).

Найти условие на параметры a,b, c , так чтобы уравнение ax2 2bxy cy2 1 задавало эллипс площади больше 1.

Справка: Площадь эллипса с полуосями A, B равна AB.

РЕШЕНИЕ. Каноническое уравнение эллипса с полуосями A,B имеет

вид	x2	y2	1.
	A2	B2

Кривая задана квадратичной формой ax2 2bxy cy2 1. Она является эллипсом, если собственные числа матрицы

			a	b	имеют один и тот же знак.
квадратичной формы					имеют один и тот же знак.

			b	c
	a	b	= ( a)( c) b2 = 2 (a c) (ac b2 ) 0 .
	a	b
	b	c

Корни 1 , 2 вычисляются через дискриминант и равны:

(a c) (a c)2 4(ac b2 )

Их произведение:


	(a c) (a c)2 4(ac b2 )									(a c) (a c)2 4(ac b2 )				=
					2								2	=
					2								2
	(a c)2 ((a c)2 4(ac b2 ))									= ac b2 >0.
					4					= ac b2 >0.
					4
При этом, после преобразования координат, уравнение эллипса
примет вид x 2						y 2 1. А поскольку каноническое уравнение
		1			1		2		1
эллипса с полуосями А,В имеет вид											x2	y2	1, то связь между
эллипса с полуосями А,В имеет вид											A2	B2	1, то связь между
											A2	B2
полуосями и собственными числами такова:
	A		1	, B		1		.
	A			, B				.
							2
		1					2

Тогда площадь эллипса:

AB=		=		1 ,	(ac b2 ) ,


	1 2		(ac b2 )
	1 2		(ac b2 )

тогда (ac b2 ) 2 .

ОТВЕТ. 0 ac b2 2 .

ЗАДАЧА 10. (Геометрия)

Уравнение однополостного гиперболоида вращения имеет вид

x2	y2	z2	1. Найти отношение	a	, при котором угол между
a2	a2	c2		c

прямолинейными образующими гиперболоида, лежащими в перпендикулярных плоскостях, составляет 30 градусов.

РЕШЕНИЕ.

Возьмѐм точки, принадлежащие гиперболоиду, на осях Ох и Оу: (a,0,0) и (0, a,0) . Прямолинейные образующие гиперболоида лежат в


вертикальных плоскостях с уравнениями x a и								y a . Подставляя в
уравнение				гиперболоида, получим уравнения				искомых прямых:
	y	z	и		x	z	. Они пересекаются там, где пересекаются две
	a	c			a	c

вертикальные плоскости, то есть над и под точкой (a, a,0) , а именно в точках (a, a,c) и (a, a, c) . Рассмотрим две образующих, которые пересекаются в точке (a, a,c) . Первая из них проходит через (a,0,0) и

(a, a,c) , значит,	направляющий вектор l1 (0, a,c) .	Вторая
образующая прямая	проходит через (0, a,0) и (a, a,c) ,	для неѐ

направляющий вектор l2 (a,0,c) . Угол между ними вычисляется

		(l1,l2 )									c	2
		(l1,l2 )									c
								arccos					.
как arccos							=	arccos			c2		.
			l	l					a	2	c2
			1		2										a 2
			1		2
									c2
									c2				3			2
Если угол 30 градусов, то														, 1			.
Если угол 30 градусов, то									a2 c2					, 1			.
									a2 c2				2		c	3

Ответ.	a	2				1 .
	c
		3
		3

Чертѐж:

<<< < Предыдущая 12 / 62 3 4 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]