
Компьютерное моделирование и проектирование
..pdfпроводить до тех пор, пока не будет достигнута оценка вида (186). Заметим, что для некоторых подинтегральных функций f (x) такое
измельчение может продолжаться слишком долго. Поэтому в соответствующей программе следует предусмотреть ограничение сверху на число измельчений, а также возможность увеличения ε .
Таким образом, автоматический выбор шага интегрирования приводит к тому, что интегрирование ведется с крупным шагом на участках плавного изменения функции f (x) и с мелким шагом – на
участках быстрого изменения f (x) . Это позволяет при заданной точности ε уменьшить количество вычислений значений f (x) по сравнению с
расчетом на сетке с постоянным шагом. Подчеркнем, что для нахождения сумм Ih / 2,i не надо пересчитывать значения f (x) во всех узлах, достаточно
вычислять f (x) только в новых узлах.
17.4 Метод Эйткена ускорения сходимости
Предположим, что какой-либо итерационный метод имеет линейную сходимость, т.е.
x |
− x ≈ aqk , q (0,1), k =1,2,... |
k |
* |
Числа a , q , x* заранее неизвестны, но их можно найти, используя три последовательных итерации xk , xk+1 , xk +2 . Составим уравнения
x − x = aqk , |
x |
− x = aqk +1 |
, |
x |
− x = aqk +2 |
|
k |
* |
k +1 |
* |
|
k +2 |
* |
(здесь равенства надо понимать как приближенные), из которых найдем
∆x |
= x |
− x = aqk (q −1), |
|
|
|
|
|
||
k |
k +1 |
k |
|
|
|
|
|
|
|
∆2 = ∆x |
− ∆x = aqk |
(q −1)2 |
= x |
− 2x |
+ x , |
||||
|
k +1 |
k |
|
|
|
k +2 |
|
k+1 |
k |
|
|
x |
|
= x |
− |
(∆x |
|
)2 |
(187) |
|
|
|
k +1 |
. |
|||||
|
|
* |
k +2 |
|
∆2 x |
|
|
||
|
|
|
|
|
|
|
k |
|
|
Метод Эйткена ускорения сходимости состоит в том, что после вычисления xk , xk+1 , xk +2 производится пересчет по формуле
yk +1 = xk +2 − |
(∆x |
)2 |
k +1 |
(188) |
|
∆2 x |
||
|
k |
|
и значение yk +1 принимается за новое приближение. Если бы равенство (187) выполнялось точно, то yk +1 совпало бы с точным решением x* . В общем случае yk+1 дает лучшее приближение к x* , чем очередная итерация
91
xk +2 . Подчеркнем, что главным предположением здесь является требование
линейной сходимости основного итерационного метода. В случае методов, имеющих более высокую скорость сходимости (например, метод Ньютона), ускорение по Эйткену в форме (188) неэффективно.
На практике необязательно проводить пересчет по формуле (188) на каждой итерации k . Употребительны методы, в которых такой пересчет осуществляется циклически, т.е. через определенное число итераций.
С помощью метода Эйткена на основе известных итерационных методов можно получить иногда новые итерационные методы, обладающие высокой сходимостью. Рассмотрим, например, метод релаксации
xk +1 − xk |
+ f (x |
) = 0 , |
(189) |
|
|||
τ |
k |
|
|
|
|
|
который имеет линейную сходимость, если
M1 > f '(x) > 0, 0 <τ < 2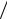 M1.
M1.
Предположим, что при некотором k получены значения xk , xk +1 , xk +2 . Вычислим согласно (188) величину
|
yk +1 = xk +2 − |
|
|
(x |
− x |
k +1 |
)2 |
|
|
|
(190) |
|||
|
|
|
k +2 |
|
|
|
|
|
||||||
|
|
xk +2 − |
2xk +1 + xk |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||
и исключим из (190) с помощью (189) величины xk +1 , xk +2 . Имеем |
|
|||||||||||||
xk +1 = xk −τ f (xk ), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xk +2 = xk+1 −τ f (xk+1) = xk −τ f (xk ) −τ f (xk −τ f (xk )), |
|
|||||||||||||
следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yk +1 = xk −τ |
|
|
|
|
f |
2 (x |
|
) |
|
|
. |
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
f (xk ) − f (xk −τ f (xk )) |
|
|
|
|||||||||
Проведенные |
построения |
|
|
позволяют |
предположить, |
что |
||||||||
одношаговый итерационный метод |
|
|
|
|
|
|
|
|
|
|
|
|||
|
yk +1 = yk −τ |
|
|
|
|
f 2 ( yk ) |
|
|
|
(191) |
||||
|
|
f |
( yk ) − f ( yk −τ f ( yk )) |
|||||||||||
|
|
|
|
|
||||||||||
обладает более быстрой сходимостью, чем исходный метод релаксации (12). Действительно, метод (191) при τ =1 (метод Стеффенсена) имеет квадратичную сходимость.
92
Список литературы
1.Основы компьютерного моделирования наносистем / Ибрагимов И.М. , Ковшов А.Н., Назаров Ю.Ф. – М.: Изд-во «Лань» , 2010.- 384 с.
ISBN 978-5-8114-1032-3:
2.Поршнев С.В. Компьютерное моделирование физических процессов в пакете MATLAB. + CD. - М.: Изд-во «Лань», 2011.- 736 с. ISBN 978-5-8114-1063-7
3.Моделирование компонентов и элементов интегральных схем /
Петров М.Н., Гудков Г.В. - М.: Изд-во «Лань», 2011.- 464 с. ISBN 978-5- 8114-1075-0
4.Основы автоматизированного проектирования [Текст] : учебник для вузов / Е. М. Кудрявцев. - М. : Академия, 2011. - 304 с. - ISBN 978-5- 7695-6004-0
5.Компьютерное моделирование и проектирование: учебное пособие
/Ю. Р. Саликаев.- Томск: ТУСУР, 2012. - 100 с. Препринт. Режим доступа:: http://edu.tusur.ru/ training/ publications/
6.Численные методы в примерах и задачах : Учебное пособие для втузов / В. И. Киреев, А. В. Пантелеев. - 2-е изд., стереотип. - М. : Высшая школа, 2006. - 479 с. - (Прикладная математика для втузов). - ISBN 5-06- 004763-6 :
7.Численные методы : Учебное пособие для втузов / В. Ф. Формалев, Д. Л. Ревизников ; ред. : А. И. Кибзун. - 2-е изд., испр. и доп. -
М. : Физматлит, 2006. - 398 с. ISBN 5-9221-0737-2
8.Основы численных методов : Учебник для вузов / Валентин Михайлович Вержбицкий. - М. : Высшая школа, 2002. - 848 с. - ISBN 5-06- 004020-8
9.Машинные методы анализа и проектирования электронных схем :
/И. Влах, К. Сингхал ; пер.: А. Ф. Объедков, Н. Н. Удалов, В. М. Демидов ;
ред. пер. А. А. Туркина. - М. : Радио и связь, 1988. - 560 с. - ISBN 5-256- 00054-3
10.Очков В. Ф. Mathcad PLUS 6.0 для студентов и инженеров. - М.: Компьюетр-Пресс, 1996. – 238 с.
11.Mathcad для студента / А. М. Половко , И. В. Ганичев. - СПб. :
БХВ-Петербург, 2006. - 336 с. - ISBN 5-94157-596-3
12Mathcad 12 для студентов и инженеров / В. Ф. Очков. - СПб. :
БХВ-Петербург, 2005. - 457 с. - ISBN 5-94157-289-1
93
Саликаев Ю.Р.
Компьютерное моделирование и проектирование
Учебное пособие
Усл. печ. л. Препринт Томский государственный университет систем управления и радиоэлектроники
634050, г.Томск, пр.Ленина, 40
