
литография / 1_4_Деструкция фоторезиста
.pdf
9. Моделирование физико-химических процессов в фоторезисте при экспонировании
Суть процесса фотолитографии состоит в переносе в слой фоторезиста изображения фотошаблона - сначала в виде скрытого изображения, а затем в виде рельефа. Для этого фотошаблон, уже содержащий требуемую топологию, освещается равномерным пучком ультрафиолетового излучения, а оптическая система передает его изображение в фоторезист. Изображение фотошаблона передается на подложку одновременно и целиком, что является важным достоинством фотолитографии, обеспечивающим высокую производительность процесса.
Профиль рельефа в фоторезисте должен отвечать чрезвычайно жестким требованиям к своей геометрии, поскольку он выполняет роль маски для последующих операций.
Как уже отмечалось, размеры элементов топологических рисунков могут быть менее 1 мкм, а их число даже одном модуле может превышать 1 миллион. Это предъявляетособые требования не только к номинальному размеру окна на поверхности подложки, но и к остаточной толщине фоторезиста, и к углу наклона профиля. Допуск на размер минимального элемента назначается в зависимости от вида последующих операций (локальное нанесение материалов или травление заготовки), однако обычно он не превышает ±15% от размера элемента с 5%-ным допуском на требуемый наклон краев.
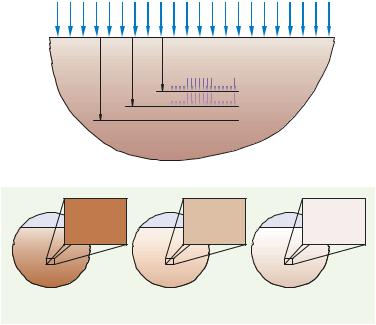
Данный раздел курса посвящен рассмотрению физических принципов формирования микроизображений методом фотолитографии. Для проведения физического анализа опишем процесс фотолитографии последовательностью наиболее важных, ключевых этапов (рис. 1):
a)
 б)
б)
 в)
в)
1. При экспонировании оптическое излучение, прошедшее сквозь фотошаблон, несет в себе информацию о топологии в виде распределения интенсивности излучения. В результате на поверхности фоторезиста формируется оптическое изображение фотошаблона (рис. 1, а).
2.Под действием излучения в фоторезисте происходят фотохимические процессы, приводящие к деструкции облученных участков (в позитивных фоторезистах) или к их полимеризации (в негативных фоторезистах). В результате в слое фоторезиста формируется скрытое изображение (рис. 1, б).
3.Проявление превращает скрытое изображение в рельеф в слое фоторезиста, который служит маской для последующих операций микрообработки - травления, напыления, гальванического осаждения и ряда других (рис. 1, в).
Для определения профиля изображения, получаемого после проявления необходимо смоделировать физико-химические процессы, происходящие в фоторезисте при экспонировании.
Поставленная нами цель – количественное описание профиля формируемого изображения – требует однозначно преобразовывать эффект (результат) оптического экспонирования в контур (профиль) поверхности фоторезиста после проявления. Поэтому мы будем далее опираться на физическое моделирование процесса, нежели на химию высокомолекулярных соединений.
Очень важным физическим параметром фоторезиста является коэффициент оптического поглощения. Дело в том, что при экспонировании слоя фоторезиста участки, расположенные на разных расстояниях от поверхности подложки, получают различные дозы экспозиции. Это объясняется сильным оптическим поглощением, связанным с фоточувствительностью резиста. Поглощение излучения определяется концентрацией ингибитора и уменьшается по мере его разрушения. Этот процесс локализован в пределах того участка фоторезиста, в котором произошло разрушение ингибитора.
Для описания этого процесса используем коэффициент поглощения α, который в данном случае будет зависеть от расположения участка фоторезиста по толщине слоя и от времени экспонирования.
Введем параметр М(z,t), характеризующий концентрацию ингибитора (для любой координаты z и времени t) по отношению к его концентрации перед экспонированием.
Пренебрегая малым рассеянием света в пленках фоторезистов можно записать следующее выражение для коэффициента поглощения:
A M z,t B |
(а) |
В этом выражении А и В – экспериментально определяемые для каждого фоторезиста параметры, характеризующие, соответственно, зависящую и независящую от экспозиции составляющие коэффициента поглощения.
Для выяснения физической сущности этих явлений и их применимости для описания процессов рассмотрим пленку фоторезиста, нанесенную на стеклянную подложку, согласованную по коэффициенту преломления n с фоторезистом. Это позволяет свести к минимуму обратное отражение в фоторезист от поверхности раздела фоторезистподложка и не учитывать интерференционные эффекты, возникающие на отражающих кремниевых подложках.
В этом случае для описания оптического поглощения можно использовать закон
Бутера-Ламберта-Бера
Уменьшение интенсивности света в слое толщиной dz пропорционально величине интенсивности падающего на этот слой света и толщине поглощающего слоя:
dI I dz ,
где α – коэффициент пропорциональности, не зависящий от интенсивности света. Знак “-” показывает, что с увеличением толщины поглощающего слоя интенсивность прошедшего через него света уменьшается.
С целью получения выражения для интенсивности прошедшего слой толщиной l света проинтегрируем (а) в пределах от 0 до l, имея в виду, что при l = 0 I = I0
I |
l |
||
|
dI |
dz |
|
I |
|||
|
0 |
||
I0 |
|||
(b)
(c)
Фоторезист является однородной средой. Поэтому коэффициент α, показывающий какую часть падающей интенсивности поглощает слой толщиной dz, не зависит ни от координаты z, ни от интенсивности I, и его можно вынести из-под знака интеграла как постоянную. Получим:
ln I |
I |
z |
d ; |
ln I -ln I0 - d . |
|
I0 |
|
0 |
|
I I0 e d .
Согласно Беру, поглощение тонким слоем пропорционально числу молекул, в нем содержащихся, а следовательно числу их в единице объема среды, то есть их концентрации:
k'n,
где n – число молекул в 1см3 среды;
k’ – молекулярный коэффициент поглощения.
ТогдаI I0 e k' n d .
Если концентрация молекул выражается числом m молей в литре раствора, то пользуются молярным коэффициентом поглощения:
.
a m k' n
тогда I I0 e a m d
Рассмотрим применение формулы Бугера – Ламберта –Бера применительно к анализу фотохимических процессов в позитивном фоторезисте, следуя общепринятой модели Dill’a. Сохраним нумерацию формул в соответствии с первоисточником.
Для нашего случая: |
dI |
I ai mi , |
(1) |
|
|||
|
dz |
|
|
где I – интенсивность излучения;
z – расстояние от поверхности раздела резист - воздух вглубь пленки резиста; mi – молярная концентрация i-ой компоненты;
ai – молярный коэффициент поглощения i-ой компоненты.
Знак “-” показывает, что при прохождении излучения по фоторезисту его интенсивность уменьшается.
В позитивном фоторезисте необходимо учитывать три поглощающих компоненты: ингибитор, базовый полимер и продукты реакции разрушения ингибитора. Экспонирование превращает ингибитор в продукты реакции, уменьшая общее поглощение пленки резиста.
Конкретизируя уравнение (1) для случая позитивного фоторезиста, получим:
|
|
|
I(z,t) |
I(z,t) a |
m (z,t) a |
|
m |
|
(z,t) |
a |
|
m (z,t) , |
(2) |
|||||||||||||||
|
|
|
|
|
|
2 |
2 |
3 |
||||||||||||||||||||
|
|
|
z |
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
3 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где |
I(z,t) – интенсивность излучения на глубине z в момент экспонирования |
|
||||||||||||||||||||||||||
|
a1, а2, а3 – молярные коэффициенты поглощения соответственно ингибитора, |
|
||||||||||||||||||||||||||
|
|
|
полимера и продуктов реакции; |
|
|
|
|
|
|
|
|
|
||||||||||||||||
m1(z,t), m2(z,t), m3(z,t) – молярные концентрации соответственно ингибитора, полимера и |
|
|||||||||||||||||||||||||||
|
|
|
продуктов реакции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Разрушение ингибитора описывается уравнением: |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
m1(z,t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m1 |
(z,t) I(z,t) C |
|
|
|
|
(3) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
где C – относительная скорость разрушения ингибитора, приходящаяся на единицу |
|||||||||||||||||||||||||||
|
интенсивности. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Введем следующие дополнительные условия и предположения: |
|
|
|||||||||||||||||||||||||
|
I(0,t)=I0 |
|
|
- постоянная интенсивность источника |
|
|
(4) |
|||||||||||||||||||||
|
m1(z,0)=m10 |
|
|
- начальная концентрация ингибитора |
|
|
(5) |
|||||||||||||||||||||
|
m2(z,t)=m20 |
|
|
- однородность и постоянство полимера, |
|
|
(6) |
|||||||||||||||||||||
|
m3(z,t)=m10-m1(z,t) |
|
|
который не осветляется при экспонировании |
||||||||||||||||||||||||
|
|
- преобразование одного моля ингибитора в 1 моль продуктов |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
реакции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(7) |
|||
|
Подставляя (4)-(7) в (2), получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
I(z,t) |
I(z,t) a |
a |
m (z,t) a |
|
m |
|
(z,t) a |
|
m , |
(8) |
||||||||||||||
|
|
|
|
|
|
2 |
|
3 |
||||||||||||||||||||
|
|
|
|
|
z |
|
|
|
|
|
|
1 |
3 |
|
1 |
|
|
|
20 |
|
10 |
|
||||||
|
Проведем нормирование: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
M(z,t) |
m1(z,t) |
|
- относительная концентрация ингибитора |
|
|
(9) |
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
m10 |
|
|
|
|
|
|
|
|
|
|
|
|
A L 1(мкм 1) |
|
|
|
|||||||||
|
|
|
A (a a |
3 |
) m |
|
|
|
|
|
|
|
(10) |
|||||||||||||||
|
|
|
|
|
|
1 |
|
|
10 |
|
|
|
|
|
B L 1(мкм 1) |
|
|
|
||||||||||
|
|
|
B a |
2 |
m |
|
a m |
|
|
|
|
|
|
(11) |
||||||||||||||
|
|
|
|
|
|
|
20 |
3 |
10 |
|
|
|
С L2 E 1(см2 /mI) |
|
|
|
||||||||||||
|
|
|
C = C |
|
|
|
|
|
|
|
|
|
|
|
|
(12) |
||||||||||||
С – относительная скорость разрушения ингибитора на единицу интенсивности (параметр чувствительности резиста).
Подставляя (9) - (12) в (2) и (3), получим основные рабочие уравнения, |
|
||||
описывающие поглощение излучения и деструкцию ингибитора: |
|
||||
|
I(z,t) |
I(z,t) A M(z,t) B |
(13) |
||
|
|
|
|||
|
|
z |
|
||
|
|
M(z,t) |
I(z,t) M(z,t) C |
(14) |
|
|
|
|
|||
|
|
t |
|
||
К этим уравнениям применимы следующие граничные условия (перед экспонированием):
M(z,0)=1; |
(15) |
И начальные условия (на разделе резист - воздух): |
|
I(0,t)=I0; |
(16) |
Условия (15)-(16) позволяют провести численное интегрирование уравнений для I(z,t) и M(z,t) при подстановке заранее определенных значений А, В, С и I0.
Для численного решения уравнений (13), (14) следует перейти от дифференциальной
I0
z+dz |
z |
z-dz |
I(z-dz,t)
I(z,t)








 I(z+dz,t)
I(z+dz,t)
M(z,t-dt) M(z,t) M(z,t+dt)
Время: t-dt |
Время: t |
Время: t+dt |
|||
формы к конечным разностям |
I |
, |
M |
. |
|
|
|
|
|||
|
z |
t |
|
||
Значения M(z,t), рассчитанные для заданной глубины и координаты ячейки, позволяют в заданный момент времени оценить скорость ее растворения V[Z,X]. Для этого используется эмпирическая формула:
V[Z,X]:=0.1*EXP(E1+E2*M[Z,X]+E3*M[Z,X]*M[Z,X]);
где E1, E2, E3 – экспериментально определяемые коэффициенты.
Контрольное задание.
1.Привести дифференциальные уравнения (13)-(14) к уравнениям в конечных разностях.
2.Разработать математическое и программное обеспечение для количественной оценки распределения молекулярной концентрации ингибитора по глубине фоторезиста ( по его подслоям).
Рекомендуется применить метод дискретной имитации экспонирования по времени, рассматривая его как квазиимпульсное.
3.Начальное условие t=0 – состояние фоторезиста до начала экспонирования.
Граничное: Z=0 – слой воздуха, граничащий с фоторезистом, Z=1 – 1-й подслой фоторезиста.
Поэтому цикл организовывать, задавая t=1 и Z=1.
4.Типовые значения коэффициентов А, В и С:
А= 0,54
В = 0,03 С = 0,014
Нормированное значение интенсивности Iо = 1.
